Article contents
Dynamics of revolving wings for various aspect ratios
Published online by Cambridge University Press: 12 May 2014
Abstract
High-fidelity, direct numerical simulations (DNSs) are conducted to examine the vortex structure and aerodynamic loading of unidirectionally revolving wings in quiescent fluid. Wings with aspect ratios 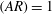 $({\mathit{AR}}) = 1$, 2 and 4 are considered at a fixed root-based Reynolds number of 1000. Each wing is shown to generate a coherent leading-edge vortex (LEV) that remains in close proximity to the surface and provides persistent suction throughout the motion. Towards the tip, the LEV lifts off as an arch-like structure and reorients itself along the chord through its connection with the tip vortex. The substantial and sustained aerodynamic loads achieved during the motion saturate with aspect ratio resulting from the chordwise growth of the LEV along the span eventually becoming geometrically constrained by the trailing edge. Further, for
$({\mathit{AR}}) = 1$, 2 and 4 are considered at a fixed root-based Reynolds number of 1000. Each wing is shown to generate a coherent leading-edge vortex (LEV) that remains in close proximity to the surface and provides persistent suction throughout the motion. Towards the tip, the LEV lifts off as an arch-like structure and reorients itself along the chord through its connection with the tip vortex. The substantial and sustained aerodynamic loads achieved during the motion saturate with aspect ratio resulting from the chordwise growth of the LEV along the span eventually becoming geometrically constrained by the trailing edge. Further, for 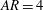 ${\mathit{AR}}=4$, substructures develop in the feeding sheet of the LEV, which appear to directly correlate with the local, span-based Reynolds number achieved during rotation. The lower-aspect-ratio wings do not have sufficient spans for these transitional elements to manifest. In contrast, vortex breakdown, which occurs around midspan for each aspect ratio, shows a strong dependence on the spanwise pressure gradient established between the root and tip of the wing and not local Reynolds number. This independent development of shear-layer substructures and vortex breakdown parallels very closely with what has been observed in delta wing flow. Next, the centrifugal, Coriolis and pressure gradient forces are also analysed at several spanwise locations across each wing, and the centrifugal and pressure gradient forces are shown to be responsible for the spanwise flow above the wing. The Coriolis force is directed away from the surface at the base of the LEV, indicating that it is not a contributor to LEV attachment, which is contrary to previous hypotheses. Finally, as a means of emphasizing the importance of the centrifugal force on LEV attachment, the
${\mathit{AR}}=4$, substructures develop in the feeding sheet of the LEV, which appear to directly correlate with the local, span-based Reynolds number achieved during rotation. The lower-aspect-ratio wings do not have sufficient spans for these transitional elements to manifest. In contrast, vortex breakdown, which occurs around midspan for each aspect ratio, shows a strong dependence on the spanwise pressure gradient established between the root and tip of the wing and not local Reynolds number. This independent development of shear-layer substructures and vortex breakdown parallels very closely with what has been observed in delta wing flow. Next, the centrifugal, Coriolis and pressure gradient forces are also analysed at several spanwise locations across each wing, and the centrifugal and pressure gradient forces are shown to be responsible for the spanwise flow above the wing. The Coriolis force is directed away from the surface at the base of the LEV, indicating that it is not a contributor to LEV attachment, which is contrary to previous hypotheses. Finally, as a means of emphasizing the importance of the centrifugal force on LEV attachment, the 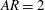 ${\mathit{AR}}=2$ wing is simulated with the addition of a source term in the governing equations to oppose and eliminate the centrifugal force near the surface. The initial formation and development of the LEV is unhindered by the absence of this force; however, later in the motion, the outboard lift-off of the LEV moves inboard. Without the opposing outboard-directed centrifugal force to keep the separation past midspan, the entire vortex eventually separates and moves away from the surface.
${\mathit{AR}}=2$ wing is simulated with the addition of a source term in the governing equations to oppose and eliminate the centrifugal force near the surface. The initial formation and development of the LEV is unhindered by the absence of this force; however, later in the motion, the outboard lift-off of the LEV moves inboard. Without the opposing outboard-directed centrifugal force to keep the separation past midspan, the entire vortex eventually separates and moves away from the surface.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 104
- Cited by


