Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T16:35:47.567Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of laterally confined marine ice sheets

Published online by Cambridge University Press:  03 February 2016

Katarzyna N. Kowal ,
Samuel S. Pegler  and
M. Grae Worster
Katarzyna N. Kowal*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, Wilberforce Road, Cambridge CB3 0WA, UK
Samuel S. Pegler
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, Wilberforce Road, Cambridge CB3 0WA, UK Queens’ College, University of Cambridge, Cambridge CB3 9ET, UK
M. Grae Worster
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an experimental and theoretical study of the dynamics of laterally confined marine ice sheets in the natural limit in which the long, narrow channel into which they flow is wider than the depth of the ice. A marine ice sheet comprises a grounded ice sheet in contact with bedrock that floats away from the bedrock at a ‘grounding line’ to form a floating ice shelf. We model the grounded ice sheet as a viscous gravity current resisted dominantly by vertical shear stresses owing to the no-slip boundary condition applied at the bedrock. We model the ice shelf as a floating viscous current resisted dominantly by horizontal shear stresses owing to no-slip boundary conditions applied at the sidewalls of the channel. The two shear-dominated regions are coupled by jump conditions relating force and fluid flux across a short transition region downstream of the grounding line. We find that the influence of the stresses within the transition region becomes negligible at long times and we model the transition region as a singular interface across which the ice thickness and mass flux can be discontinuous. The confined shelf buttresses the sheet, causing the grounding line to advance more than it would otherwise. In the case that the sheet flows on a base of uniform slope, we find asymptotically that the grounding line advances indefinitely as 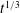$t^{1/3}$, where $t$ is time. This contrasts with the two-dimensional counterpart, for which the shelf provides no buttressing and the grounding line reaches a steady state (Robison, J. Fluid Mech., vol. 648, 2010, pp. 363–380).

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Ice sheets
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 790 , 10 March 2016 , R2
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acton, J. M., Huppert, H. E. & Worster, M. G. 2001 Two-dimensional viscous gravity currents flowing over a deep porous medium. J. Fluid Mech. 440, 359–380.CrossRefGoogle Scholar
Dupont, T. K. & Alley, R. B. 2005 Assessment of the importance of ice-shelf buttressing to ice-sheet flow. Geophys. Res. Lett. 32, L04503.CrossRefGoogle Scholar
Glen, J. W. 1955 The creep of polycrystalline ice. Proc. R. Soc. Lond. A 228, 519–538.Google Scholar
Gudmundsson, G. H. 2013 Ice-shelf buttressing and the stability of marine ice sheets. Cryosphere 7, 647–655.CrossRefGoogle Scholar
Hambrey, M. & Alean, J. 2004 Glaciers, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Huppert, H. E. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.CrossRefGoogle Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.CrossRefGoogle Scholar
Pegler, S. S.2012 The fluid mechanics of ice-shelf buttressing. PhD thesis, University of Cambridge.Google Scholar
Pegler, S. S. 2016 Confined extensional flows. J. Fluid Mech., sub judice.CrossRefGoogle Scholar
Pegler, S. S., Kowal, K. N., Hasenclever, L. Q. & Worster, M. G. 2013 Lateral controls on grounding-line dynamics. J. Fluid Mech. 722, R1.CrossRefGoogle Scholar
Pegler, S. S. & Worster, M. G. 2013 An experimental and theoretical study of the dynamics of grounding lines. J. Fluid Mech. 728, 5–28.CrossRefGoogle Scholar
Robison, R. A. V., Huppert, H. E. & Worster, M. G. 2010 Dynamics of viscous grounding lines. J. Fluid Mech. 648, 363–380.CrossRefGoogle Scholar
Schoof, C. 2007 Ice sheet grounding line dynamics: steady states, stability, and hysteresis. J. Geophys. Res. 112, f03S28.CrossRefGoogle Scholar
Weertman, J. 1974 Stability of the junction of an ice sheet and an ice shelf. J. Glaciol. 13 (67), 3–13.CrossRefGoogle Scholar
Wilchinsky, A. V. & Chugunov, V. A. 2000 Ice-stream–ice-shelf transition: theoretical analysis of two-dimensional flow. Ann. Glaciol. 30, 153–162.CrossRefGoogle Scholar
Supplementary material: File

Kowal Supplementary Material

Experiments

Download Kowal Supplementary Material(File)
File 47.1 KB

Kowal Supplementary Material

Movie 1

Download Kowal Supplementary Material(Video)
Video 8.6 MB

Kowal Supplementary Material

Movie 2

Download Kowal Supplementary Material(Video)
Video 2 MB