Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-02T22:03:01.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of hemiwicking

Published online by Cambridge University Press:  29 June 2016

Jungchul Kim ,
Myoung-Woon Moon  and
Ho-Young Kim
Jungchul Kim
Affiliation:
Department of Mechanical and Aerospace Engineering, Seoul National University, Seoul 08826, Korea
Myoung-Woon Moon
Affiliation:
Computational Science Research Center, Korea Institute of Science and Technology, Seoul 02792, Korea
Ho-Young Kim*
Affiliation:
Department of Mechanical and Aerospace Engineering, Seoul National University, Seoul 08826, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Hemiwicking refers to the spreading of a liquid on a rough hydrophilic surface driven by capillarity. Here, we construct scaling laws to predict the velocity of hemiwicking on a rough substrate and experimentally corroborate them with various arrangements and dimensions of micropillar arrays. At the macroscopic scale, where the wetting front appears parallel to the free surface of the reservoir, the wicking distance is shown to grow diffusively, i.e. 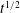like $t^{1/2}$ with $t$ being time. We show that our model is consistent with pillar arrays of a wide range of pitch-to-height ratios, either square or skewed. At the microscopic scale, where the meniscus extension from individual pillars at the wetting front is considered, the extension distance begins to grow like $t$ but the spreading slows down to behave like 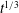$t^{1/3}$ when the meniscus is far from the pillar. Our microscopic flow modelling allows us to find pillar spacing conditions under which the assumption of densely spaced pillars is valid.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Interfacial Flows (free surface) Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 800 , 10 August 2016 , pp. 57 - 71
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bico, J., Thiele, U. & Quéré, D. 2002 Wetting of textured surfaces. Colloids Surf. A 206, 41–46.CrossRefGoogle Scholar
Bico, J., Tordeus, C. & Quéré, D. 2001 Rough wetting. Europhys. Lett. 55, 214–220.CrossRefGoogle Scholar
Courbin, L., Denieul, E., Dressaire, E., Roper, M., Ajdari, A. & Stone, H. A. 2007 Imbibition by polygonal spreading on microdecorated surfaces. Nat. Mater. 6, 661–664.CrossRefGoogle ScholarPubMed
Hasimoto, H. 1959 On the periodic fundamental solutions of the Stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5, 317–328.Google Scholar
Ishino, C., Reyssat, M., Reyssat, E., Okumura, K. & Quéré, D. 2007 Wicking within forests of micropillars. Europhys. Lett. 79, 56005.CrossRefGoogle Scholar
Kim, H.-Y., Lee, H. J. & Kang, B. H. 2003 Sliding of liquid drops down an inclined solid surface. J. Colloid Interface Sci. 247, 372–380.Google Scholar
Kim, J., Moon, M.-W., Lee, K.-R., Mahadevan, L. & Kim, H.-Y. 2011b Hydrodynamics of writing with ink. Phys. Rev. Lett. 107, 264501.Google Scholar
Kim, S. J., Choi, J. W., Moon, M.-W., Lee, K.-R., Chang, Y. S., Lee, D.-Y. & Kim, H.-Y. 2015 Wicking and flooding of liquids on vertical porous sheets. Phys. Fluids 27, 032105.Google Scholar
Kim, S. J., Moon, M.-W., Lee, K.-R., Lee, D.-Y., Chang, Y. S. & Kim, H.-Y. 2011a Liquid spreading on superhydrophilic micropillar arrays. J. Fluid Mech. 680, 477–487.CrossRefGoogle Scholar
Lee, A. & Kim, H.-Y. 2012 Water harvest via dewing. Langmuir 28, 10183–10191.Google Scholar
Mahadevan, L. & Pomeau, Y. 1999 Rolling droplets. Phys. Fluids 11, 2449–2453.Google Scholar
Martinez, A. W., Phillips, S. T. & Whitesides, G. M. 2008 Three-dimensional microfluidic devices fabricated in layered paper and tape. Proc. Natl. Acad. Sci. USA 105, 19606–19611.Google Scholar
Richard, D., Clanet, C. & Quéré, D. 2002 Contact time of a bouncing drop. Nature 417, 811.Google Scholar
Richard, D. & Quéré, D. 1999 Viscous drops rolling on a tilted non-wettable solid. Europhys. Lett. 48, 286–291.CrossRefGoogle Scholar
Srivastava, N., Din, C., Judson, A., MacDonald, N. C. & Meinhart, C. D. 2010 A unified scaling model for flow through a lattice of microfabricated posts. Lab on a Chip 10, 1148–1152.Google Scholar
Tsai, P., Pacheco, S., Pirat, C., Lefferts, L. & Lohse, D. 2009 Drop impact upon micro-nanostructured superhydrophobic surfaces. Langmuir 25, 12293–12298.Google Scholar
Washburn, E. W. 1921 The dynamics of capillary flow. Phys. Rev. 17, 273–283.Google Scholar
Xiao, R., Enright, R. & Wang, E. N. 2010 Prediction and optimization of liquid propagation in micropillar arrays. Langmuir 26, 15070–15075.Google Scholar
Yi, J. W., Moon, M.-W., Ahmded, S. F., Kim, H., Cha, T.-G., Kim, H.-Y., Kim, S.-S. & Lee, K.-R. 2010 Long-lasting hydrophilicity on nanostructured Si-incorporated diamond-like carbon films. Langmuir 26, 17203–17209.CrossRefGoogle ScholarPubMed