Article contents
Dynamics of forced and unforced autophoretic particles
Published online by Cambridge University Press: 14 September 2022
Abstract
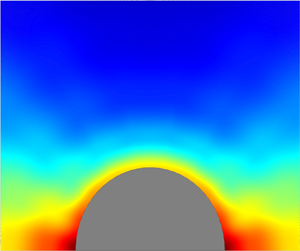
Chemically active, or autophoretic, particles that isotropically emit or absorb solute molecules undergo spontaneous self-propulsion when their activity is increased beyond a critical Péclet number ( $Pe$). Here, we conduct numerical computations, using a spectral element based method, of a rigid, spherical autophoretic particle in unsteady rectilinear translation. The particle can be freely suspended (or ‘unforced’) or subject to an external force field (or ‘forced’). The motion of an unforced particle progresses through four regimes as
$Pe$). Here, we conduct numerical computations, using a spectral element based method, of a rigid, spherical autophoretic particle in unsteady rectilinear translation. The particle can be freely suspended (or ‘unforced’) or subject to an external force field (or ‘forced’). The motion of an unforced particle progresses through four regimes as  $Pe$ is increased: quiescent, steady, stirring and chaos. The particle is stationary in the quiescent regime, and the solute profile is isotropic about the particle. At
$Pe$ is increased: quiescent, steady, stirring and chaos. The particle is stationary in the quiescent regime, and the solute profile is isotropic about the particle. At  $Pe=4$ the fore–aft symmetry in the solute profile is broken, resulting in its steady self-propulsion. Our computations indicate that the self-propulsion speed scales linearly with
$Pe=4$ the fore–aft symmetry in the solute profile is broken, resulting in its steady self-propulsion. Our computations indicate that the self-propulsion speed scales linearly with  $Pe-4$ near the onset of self-propulsion, as has been predicted in previous studies. A further increase in
$Pe-4$ near the onset of self-propulsion, as has been predicted in previous studies. A further increase in  $Pe$ gives rise to the stirring regime at
$Pe$ gives rise to the stirring regime at  $Pe\approx 27$, where the fluid undergoes recirculation, while the particle remains essentially stationary. As
$Pe\approx 27$, where the fluid undergoes recirculation, while the particle remains essentially stationary. As  $Pe$ is increased even further, the particle dynamics is marked by chaotic oscillations at
$Pe$ is increased even further, the particle dynamics is marked by chaotic oscillations at  $Pe\approx 55$ and higher, which we characterize in terms of the mean square displacement and velocity autocorrelation of the particle. Our results for an autophoretic particle under a weak external force are in good agreement with recent asymptotic predictions (Saha, Yariv & Schnitzer, J. Fluid Mech., vol. 916, 2021, p. A47). Additionally, we demonstrate that the strength and temporal scheduling of the external force may be tuned to modulate the chaotic dynamics at large
$Pe\approx 55$ and higher, which we characterize in terms of the mean square displacement and velocity autocorrelation of the particle. Our results for an autophoretic particle under a weak external force are in good agreement with recent asymptotic predictions (Saha, Yariv & Schnitzer, J. Fluid Mech., vol. 916, 2021, p. A47). Additionally, we demonstrate that the strength and temporal scheduling of the external force may be tuned to modulate the chaotic dynamics at large  $Pe$.
$Pe$.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 13
- Cited by



