Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T20:06:22.692Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of elastic dumbbells sedimenting in a viscous fluid: oscillations and hydrodynamic repulsion

Published online by Cambridge University Press:  12 February 2015

Marek Bukowicki ,
Marta Gruca  and
Maria L. Ekiel-Jeżewska
Marek Bukowicki
Affiliation:
Institute of Fundamental Technological Research, Polish Academy of Sciences, 02-106 Warsaw, Pawińskiego 5b, Poland
Marta Gruca
Affiliation:
Institute of Fundamental Technological Research, Polish Academy of Sciences, 02-106 Warsaw, Pawińskiego 5b, Poland
Maria L. Ekiel-Jeżewska*
Affiliation:
Institute of Fundamental Technological Research, Polish Academy of Sciences, 02-106 Warsaw, Pawińskiego 5b, Poland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Hydrodynamic interactions between two identical elastic dumbbells settling under gravity in a viscous fluid at low Reynolds number are investigated using the point-particle model. The evolution of a benchmark initial configuration is studied, in which the dumbbells are vertical and their centres are aligned horizontally. Rigid dumbbells and pairs of separate beads starting from the same positions tumble periodically while settling. We find that elasticity (which breaks the time-reversal symmetry of the motion) significantly affects the system dynamics. This is remarkable when taking into account that elastic forces are always much smaller than gravity. We observe oscillating motion of the elastic dumbbells, which tumble and change their length non-periodically. Independently of the value of the spring constant, a horizontal hydrodynamic repulsion appears between the dumbbells: their centres of mass move apart from each other horizontally. This motion is fast for moderate values of the spring constant 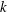$k$, and slows down when 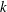$k$ tends to zero or to infinity; in these limiting cases we recover the periodic dynamics reported in the literature. For moderate values of the spring constant, and different initial configurations, we observe the existence of a universal time-dependent solution to which the system converges after an initial relaxation phase. The tumbling time and the width of the trajectories in the centre-of-mass frame increase with time. In addition to its fundamental significance, the benchmark solution presented here is important to understanding general features of systems with a larger number of elastic particles, in regular and random configurations.

JFM classification

Complex Fluids: Complex Fluids Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Stokesian dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 95 - 108
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brenner, H. 1973 Rheology of a dilute suspension of axisymmetric Brownian particles. Intl J. Multiphase Flow 1, 216–223.Google Scholar
Bustamante, C., Smith, S. B., Liphardt, J. & Smith, D. 2000 Single-molecule studies of DNA mechanics. Curr. Opin. Struct. Biol. 10, 279–285.CrossRefGoogle ScholarPubMed
Caflisch, R. E., Lim, C., Luke, J. H. C. & Sangani, A. S. 1988 Periodic solutions for three sedimenting spheres. Phys. Fluids 31, 3175–3179.CrossRefGoogle Scholar
Drescher, K., Leptos, K. C., Tuval, I., Ishikawa, T., Pedley, T. J. & Goldstein, R. E. 2009 Dancing volvox: hydrodynamic bound states of swimming algae. Phys. Rev. Lett. 102, 168101.Google Scholar
Dreyfus, R., Baudry, J., Roper, M. L., Fermigier, M., Stone, H. A. & Bibette, J. 2005 Microscopic artificial swimmers. Nature 437, 862–865.CrossRefGoogle ScholarPubMed
Ekiel-Jeżewska, M. L. 2008 Periodic orbits of Stokesian dynamics. In CDROM Proceedings of the XXII International Congress of Theoretical and Applied Mechanics (ed. Denier, J., Find, M. D. & Mattner, T.). University of Adelaide; ISBN: 978-0-9805142-1-6.Google Scholar
Ekiel-Jeżewska, M. L. 2014 Class of periodic and quasiperiodic trajectories of particles settling under gravity in a viscous fluid. Phys. Rev. E 90, 043007.CrossRefGoogle Scholar
Ekiel-Jeżewska, M. L. & Sikora, M. 2010 Periodic orbits of four point-particles settling under gravity in a viscous fluid. In Microhydrodynamics: Educational website, http://hydro.ippt.gov.pl/index.php/en/theory/49.html.Google Scholar
Farutin, A. & Misbah, C. 2013 Analytical and numerical study of three main migration laws for vesicles under flow. Phys. Rev. Lett. 110, 108104.CrossRefGoogle ScholarPubMed
Felderhof, B. U. 1988 Many-body hydrodynamic interactions in suspensions. Physica A 151, 1–16.Google Scholar
Hocking, L. M. 1963 The behaviour of clusters of spheres falling in a viscous fluid. J. Fluid Mech. 20, 129–139.Google Scholar
Holzer, L. & Zimmermann, W. 2006 Particles held by springs in a linear shear flow exhibit oscillatory motion. Phys. Rev. E 73, 060801.Google Scholar
Janosi, I. M., Tel, T., Wolf, D. E. & Gallas, J. A. C. 1997 Chaotic particle dynamics in viscous flows: The three-particle Stokeslet problem. Phys. Rev. E. 56, 2858–2868.CrossRefGoogle Scholar
Jayaweera, K. O. L. F., Mason, B. J. & Slack, G. W. 1964 The behaviour of clusters of spheres falling in a viscous fluid. Part 1. Experiment. J. Fluid Mech. 20, 121–128.Google Scholar
Jeffery, G. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Jendrejack, R. M., Schwartz, D. C., Pablo, J. J. & Graham, M. D. 2003 Shear-induced migration in flowing polymer solutions: simulation of long-chain DNA in microchannels. J. Chem. Phys. 120, 5.Google Scholar
Jung, S., Spagnolie, S. E., Prikh, K., Shelley, M. & Tornberg, A. K. 2006 Periodic sedimentation in a Stokesian fluid. Phys. Rev. E 74, 035302(R).Google Scholar
Kantsler, V. & Goldstein, R. E. 2012 Dynamics, and the stretch-coil transition of single actin filaments in extensional flows. Phys. Rev. Lett. 108, 038103.CrossRefGoogle ScholarPubMed
Kim, S. & Karrila, S. J. 2005 Microhydrodynamics. Principles and Selected Applications. Dover.Google Scholar
Ma, H. & Graham, M. D. 2004 Theory of shear – induced migration in dilute polymer solutions near solid boundaries. Phys. Fluids 17, 083103.Google Scholar
Shaqfeh, E. S. G. 2004 The dynamics of single – molecule DNA in flow. J. Non-Newtonian Fluid Mech. 130, 1–28.Google Scholar
Słowicka, A. M., Wajnryb, E. & Ekiel-Jeżewska, M. L. 2013 Lateral migration of flexible fibers in Poiseuille flow between two parallel planar solid walls. Eur. Phys. J. E 36, 1–12.CrossRefGoogle ScholarPubMed
Tory, E. M., Kamel, M. T. & Tory, C. B. 1991 Sedimentation of clusters of identical spheres. III. Periodic motion of four spheres. Powder Technol. 67, 71–82.Google Scholar
Vlahovska, P. M., Podgorski, T. & Misbah, C. 2009 Vesicles and red blood cells in flow: from individual dynamics to rheology. C. R. Phys. 10, 775–789.Google Scholar
Young, Y. N. & Shelley, M. J. 2007 Stretch-coil transition and transport of fibers in cellular flows. Phys. Rev. Lett. 99, 058303.Google Scholar

Bukowicki et al. supplementary movie

Two elastic dumbbells with the spring constant k=0.01, settling under gravity in a viscous fluid. Movie, based on the point-particle model, is taken in the centre-of-mass reference frame, for two initial configurations with the aspect ratios Cin=1 and Cin=1.8. Initially, the spring length L=1 (the equilibrium value). Hydrodynamic repulsion of the dumbbells and oscillations of their lengths are visible.

Download Bukowicki et al. supplementary movie(Video)
Video 8.4 MB

Bukowicki et al. supplementary movie

Two elastic dumbbells with the spring constant k=0.01, settling under gravity in a viscous fluid. Movie, based on the point-particle model, is taken in the centre-of-mass reference frame, for two initial configurations with the aspect ratios Cin=1 and Cin=1.8. Initially, the spring length L=1 (the equilibrium value). Hydrodynamic repulsion of the dumbbells and oscillations of their lengths are visible.

Download Bukowicki et al. supplementary movie(Video)
Video 2.2 MB

Bukowicki et al. supplementary movie

Two elastic dumbbells with the spring constant k=0.1, settling under gravity in a viscous fluid. Movie, based on the point-particle model, is taken in the centre-of-mass reference frame, for two initial configurations with the aspect ratios Cin=1 and Cin=1.8. Initially, the spring length L=1 (the equilibrium value). Hydrodynamic repulsion of the dumbbells and oscillations of their lengths are visible.

Download Bukowicki et al. supplementary movie(Video)
Video 9 MB

Bukowicki et al. supplementary movie

Two elastic dumbbells with the spring constant k=0.1, settling under gravity in a viscous fluid. Movie, based on the point-particle model, is taken in the centre-of-mass reference frame, for two initial configurations with the aspect ratios Cin=1 and Cin=1.8. Initially, the spring length L=1 (the equilibrium value). Hydrodynamic repulsion of the dumbbells and oscillations of their lengths are visible.

Download Bukowicki et al. supplementary movie(Video)
Video 2.2 MB