Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Theofanous, Theo G.
and
Chang, Chih-Hao
2017.
The dynamics of dense particle clouds subjected to shock waves. Part 2. Modeling/numerical issues and the way forward.
International Journal of Multiphase Flow,
Vol. 89,
Issue. ,
p.
177.
DeMauro, Edward P.
Wagner, Justin L.
DeChant, Lawrence J.
Beresh, Steven J.
Farias, Paul
Turpin, Aaron
Sealy, William
Albert, Samuel
and
Sanderson, Patrick
2017.
Measurements of the Initial Transient of a Dense Particle Curtain Following Shock Wave Impingement.
DeMauro, Edward P.
Wagner, Justin L.
Beresh, Steven J.
and
Farias, Paul A.
2017.
Unsteady drag following shock wave impingement on a dense particle curtain measured using pulse-burst PIV.
Physical Review Fluids,
Vol. 2,
Issue. 6,
Lv, Hua
Wang, Zhongqi
Zhang, Yunming
and
Li, Jianping
2018.
Shock attenuation by densely packed micro-particle wall.
Experiments in Fluids,
Vol. 59,
Issue. 9,
Hosseinzadeh-Nik, Zahra
Subramaniam, Shankar
and
Regele, Jonathan D.
2018.
Investigation and quantification of flow unsteadiness in shock-particle cloud interaction.
International Journal of Multiphase Flow,
Vol. 101,
Issue. ,
p.
186.
Deng, Xiaolong
Jiang, Lingjie
and
Ding, Yang
2018.
Direct Numerical Simulation of Long-term Shock-particle Curtain Interaction.
Theofanous, Theo G.
Mitkin, Vladimir
and
Chang, Chih-Hao
2018.
Shock dispersal of dilute particle clouds.
Journal of Fluid Mechanics,
Vol. 841,
Issue. ,
p.
732.
Marjanovic, Goran
Hackl, Jason
Shringarpure, Mrugesh
Annamalai, Subramanian
Jackson, Thomas L.
and
Balachandar, S.
2018.
Inviscid simulations of expansion waves propagating into structured particle beds at low volume fractions.
Physical Review Fluids,
Vol. 3,
Issue. 9,
Sugiyama, Y.
Izumo, M.
Ando, H.
and
Matsuo, A.
2018.
Two-dimensional explosion experiments examining the interaction between a blast wave and a sand hill.
Shock Waves,
Vol. 28,
Issue. 3,
p.
627.
Fox, Rodney O.
2019.
A kinetic-based hyperbolic two-fluid model for binary hard-sphere mixtures.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
282.
DeMauro, Edward P.
Wagner, Justin L.
DeChant, Lawrence J.
Beresh, Steven J.
and
Turpin, Aaron M.
2019.
Improved scaling laws for the shock-induced dispersal of a dense particle curtain.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
p.
881.
Sugiyama, Y.
Ando, H.
Shimura, K.
and
Matsuo, A.
2019.
Numerical investigation of the interaction between a shock wave and a particle cloud curtain using a CFD–DEM model.
Shock Waves,
Vol. 29,
Issue. 4,
p.
499.
Lynch, Kyle P.
and
Wagner, Justin L.
2019.
A free-piston driven shock tube for generating extreme aerodynamic environments.
Osnes, Andreas Nygård
Vartdal, Magnus
Omang, Marianne Gjestvold
and
Reif, Bjørn Anders Pettersson
2020.
Particle-resolved simulations of shock-induced flow through particle clouds at different Reynolds numbers.
Physical Review Fluids,
Vol. 5,
Issue. 1,
Gai, G.
Thomine, O.
Kudriakov, S.
and
Hadjadj, A.
2020.
A new formulation of a spray dispersion model for particle/droplet-laden flows subjected to shock waves.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Gai, Guodong
Thomine, Olivier
Hadjadj, Abdellah
and
Kudriakov, Sergey
2020.
Modeling of particle cloud dispersion in compressible gas flows with shock waves.
Physics of Fluids,
Vol. 32,
Issue. 2,
Petter, Samuel J.
Lynch, Kyle P.
Farias, Paul
Spitzer, Seth
Grasser, Thomas
and
Wagner, Justin L.
2020.
Early Experiments on Shock-Particle Interactions in the High-Temperature Shock Tube.
Peng, Xu
Rao, Guoning
Li, Bin
Wang, Shunyao
and
Chen, Wanghua
2020.
Investigation on the Gas–Solid Two-Phase Flow in the Interaction between Plane Shock Wave and Quartz Sand Particles.
Applied Sciences,
Vol. 10,
Issue. 24,
p.
8859.
Daniel, Kyle
Farias, Paul
and
Wagner, Justin L.
2021.
The Shock-Induced Disperal of Dense Particle Curtains with Varying Density.
Lv, Hua
Wang, Zhongqi
Zhang, Yunming
Li, Jianping
and
Ming, FuRen
2021.
Initial Moving Mechanism of Densely‐Packed Particles Driven by a Planar Shock Wave.
Shock and Vibration,
Vol. 2021,
Issue. 1,
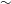 ${\sim}$1 mm) are fixed, as is the curtain thickness (
${\sim}$1 mm) are fixed, as is the curtain thickness (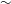 ${\sim}$30 mm) and the particle volume fractions in it, varying from
${\sim}$30 mm) and the particle volume fractions in it, varying from 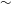 ${\sim}$58 % at the top of the curtain to
${\sim}$58 % at the top of the curtain to 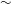 ${\sim}$24 % near the bottom. Thus, the principal experimental variable is the impacting shock strength, with Mach numbers varying from 1.2 to 2.6, and flow speeds that cover from subsonic (
${\sim}$24 % near the bottom. Thus, the principal experimental variable is the impacting shock strength, with Mach numbers varying from 1.2 to 2.6, and flow speeds that cover from subsonic (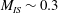 $M_{IS}\sim 0.3$) to transonic and supersonic (
$M_{IS}\sim 0.3$) to transonic and supersonic (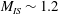 $M_{IS}\sim 1.2$). The peak shock pressure ratio, 7.6, yields a flow speed of
$M_{IS}\sim 1.2$). The peak shock pressure ratio, 7.6, yields a flow speed of 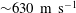 ${\sim}\!630~\text{m}~\text{s}^{-1}$, and a curtain expansion rate at
${\sim}\!630~\text{m}~\text{s}^{-1}$, and a curtain expansion rate at 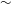 ${\sim}$20 000 g. We record visually (high-speed, particle-resolving shadowgraphic method) the reflected/transmitted pressure waves and the transmitted contact wave, as well as the curtain displacements, and we measure the reflected/transmitted pressure transients. Data analysis yields simple rules for the amplitudes of the reflected pressure waves and the rapid cloud expansions observed, and we discover a time scaling that hints at a universal regime for cloud expansion. The data and these data-analysis results can provide the validation basis for numerical simulations meant to enable a deeper understanding of the key physics that drive this rather complex dispersal process.
${\sim}$20 000 g. We record visually (high-speed, particle-resolving shadowgraphic method) the reflected/transmitted pressure waves and the transmitted contact wave, as well as the curtain displacements, and we measure the reflected/transmitted pressure transients. Data analysis yields simple rules for the amplitudes of the reflected pressure waves and the rapid cloud expansions observed, and we discover a time scaling that hints at a universal regime for cloud expansion. The data and these data-analysis results can provide the validation basis for numerical simulations meant to enable a deeper understanding of the key physics that drive this rather complex dispersal process.