Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T04:52:43.399Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of capsules enclosing viscoelastic fluid in simple shear flow

Published online by Cambridge University Press:  14 February 2018

Zheng Yuan Luo Open the ORCID record for Zheng Yuan Luo [Opens in a new window]  and
Bo Feng Bai
Zheng Yuan Luo
Affiliation:
State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China
Bo Feng Bai*
Affiliation:
State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Previous studies on capsule dynamics in shear flow have dealt with Newtonian fluids, while the effect of fluid viscoelasticity remains an unresolved fundamental question. In this paper, we report a numerical investigation of the dynamics of capsules enclosing a viscoelastic fluid and which are freely suspended in a Newtonian fluid under simple shear. Systematic simulations are performed at small but non-zero Reynolds numbers (i.e. 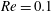$Re=0.1$) using a three-dimensional front-tracking finite-difference model, in which the fluid viscoelasticity is introduced via the Oldroyd-B constitutive equation. We demonstrate that the internal fluid viscoelasticity presents significant effects on the deformation behaviour of initially spherical capsules, including transient evolution and equilibrium values of their deformation and orientation. Particularly, the capsule deformation decreases slightly with the Deborah number De increasing from 0 to 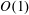$O(1)$. In contrast, with De increasing within high levels, i.e. 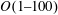$O(1{-}100)$, the capsule deformation increases continuously and eventually approaches the Newtonian limit having a viscosity the same as the Newtonian part of the viscoelastic capsule. By analysing the viscous stress, pressure and viscoelastic stress acting on the capsule membrane, we reveal that the mechanism underlying the effects of the internal fluid viscoelasticity on the capsule deformation is the alterations in the distribution of the viscoelastic stress at low De and its magnitude at high De, respectively. Furthermore, we find some new features in the dynamics of initially non-spherical capsules induced by the internal fluid viscoelasticity. Particularly, the transition from tumbling to swinging of oblate capsules can be triggered at very high viscosity ratios by increasing De alone. Besides, the critical viscosity ratio for the tumbling-to-swinging transition is remarkably enlarged with De increasing at relatively high levels, i.e. 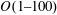$O(1{-}100)$, while it shows little change at low De, i.e. below 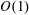$O(1)$.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Capsule/cell dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 656 - 687
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aggarwal, N. & Sarkar, K. 2007 Deformation and breakup of a viscoelastic drop in a newtonian matrix under steady shear. J. Fluid Mech. 584, 1–21.Google Scholar
Bagchi, P. & Kalluri, R. M. 2009 Dynamics of nonspherical capsules in shear flow. Phys. Rev. E 80, 016307.Google Scholar
Bai, B. F., Luo, Z. Y., Wang, S. Q., He, L., Lu, T. J. & Xu, F. 2013 Inertia effect on deformation of viscoelastic capsules in microscale flows. Microfluid. Nanofluid. 14, 817–829.Google Scholar
Barthes-Biesel, D. 1980 Motion of a spherical microcapsule freely suspended in a linear shear flow. J. Fluid Mech. 100, 831–853.Google Scholar
Barthes-Biesel, D. 2009 Capsule motion in flow: deformation and membrane buckling. C. R. Phys. 10, 764–774.Google Scholar
Barthes-Biesel, D. 2011 Modeling the motion of capsules in flow. Curr. Opin. Colloid Interface Sci. 16, 3–12.Google Scholar
Barthes-Biesel, D. 2016 Motion and deformation of elastic capsules and vesicles in flow. Annu. Rev. Fluid Mech. 48, 25–52.Google Scholar
Barthes-Biesel, D., Diaz, A. & Dhenin, E. 2002 Effect of constitutive laws for two-dimensional membranes on flow-induced capsule deformation. J. Fluid Mech. 460, 211–222.Google Scholar
Barthes-Biesel, D. & Rallison, J. M. 1981 The time-dependent deformation of a capsule freely sespended in a linear shear flow. J. Fluid Mech. 113, 251–267.Google Scholar
Chang, K.-C., Tees, D. F. & Hammer, D. A. 2000 The state diagram for cell adhesion under flow: Leukocyte rolling and firm adhesion. Proc. Natl Acad. Sci. USA 97, 11262–11267.Google Scholar
Chinyoka, T., Renardy, Y., Renardy, M. & Khismatullin, D. 2005 Two-dimensional study of drop deformation under simple shear for oldroyd-b liquids. J. Non-Newtonian Fluid Mech. 130, 45–56.Google Scholar
Cordasco, D. & Bagchi, P. 2013 Orbital drift of capsules and red blood cells in shear flow. Phys. Fluids 25, 091902.Google Scholar
de Loubens, C., Deschamps, J., Edwards-Levy, F. & Leonetti, M. 2016 Tank-treading of microcapsules in shear flow. J. Fluid Mech. 789, 750–767.Google Scholar
Dodson, W. R. & Dimitrakopoulos, P. 2009 Dynamics of strain-hardening and strain-softening capsules in strong planar extensional flows via an interfacial spectral boundary element algorithm for elastic membranes. J. Fluid Mech. 641, 263–296.Google Scholar
Dong, C. & Skalak, R. 1992 Leukocyte deformability: finite element modeling of large viscoelastic deformation. J. Theor. Biol. 158, 173–193.Google Scholar
Dong, C., Skalak, R., Sung, K.-L. P., Schmid-Schonbein, G. & Chien, S. 1988 Passive deformation analysis of human leukocytes. Trans. ASME J. Biomech. Engng 110, 27–36.Google Scholar
Dupont, C., Delahaye, F., Barthes-Biesel, D. & Salsac, A. V. 2016 Stable equilibrium configurations of an oblate capsule in simple shear flow. J. Fluid Mech. 791, 738–757.Google Scholar
Dupont, C., Salsac, A. V. & Barthes-Biesel, D. 2013 Off-plane motion of a prolate capsule in shear flow. J. Fluid Mech. 721, 180–198.Google Scholar
Dupont, C., Salsac, A. V., Barthes-Biesel, D., Vidrascu, M. & Le Tallec, P. 2015 Influence of bending resistance on the dynamics of a spherical capsule in shear flow. Phys. Fluids 27, 051902.Google Scholar
Fattal, R. & Kupferman, R. 2005 Time-dependent simulation of viscoelastic flows at high weissenberg number using the log-conformation representation. J. Non-Newtonian Fluid Mech. 126, 23–37.CrossRefGoogle Scholar
Finken, R., Kessler, S. & Seifert, U. 2011 Micro-capsules in shear flow. J. Phys. Condens. Matter 23, 184113.Google Scholar
Foessel, E., Walter, J., Salsac, A. V. & Barthes-Biesel, D. 2011 Influence of internal viscosity on the large deformation and buckling of a spherical capsule in a simple shear flow. J. Fluid Mech. 672, 477–486.Google Scholar
Forsyth, A. M., Wan, J., Owrutsky, P. D., Abkarian, M. & Stone, H. A. 2011 Multiscale approach to link red blood cell dynamics, shear viscosity, and atp release. Proc. Natl Acad. Sci. USA 108, 10986–10991.Google Scholar
Freund, J. B. 2014 Numerical simulation of flowing blood cells. Annu. Rev. Fluid Mech. 46, 67–95.Google Scholar
Guido, S. 2011 Shear-induced droplet deformation: effects of confined geometry and viscoelasticity. Curr. Opin. Colloid Interface Sci. 16, 61–70.Google Scholar
Hammer, D. A. 2014 Adhesive dynamics. Trans. ASME J. Biomech. Engng 136, 021006.Google Scholar
Helfrich, W. 1973 Elastic propeties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C 28, 693–703.Google Scholar
Huang, H., Yu, Y., Hu, Y., He, X., Usta, O. B. & Yarmush, M. L. 2017 Generation and manipulation of hydrogel microcapsules by droplet-based microfluidics for mammalian cell culture. Lab on a Chip 17, 1913–1932.Google Scholar
Izbassarov, D. & Muradoglu, M. 2015 A front-tracking method for computational modeling of viscoelastic two-phase flow systems. J. Non-Newtonian Fluid Mech. 223, 122–140.Google Scholar
Izbassarov, D. & Muradoglu, M. 2016 A computational study of two-phase viscoelastic systems in a capillary tube with a sudden contraction/expansion. Phys. Fluids 28, 012110.Google Scholar
James, D. F. 2009 Boger fluids. Annu. Rev. Fluid Mech. 41, 129–142.Google Scholar
Keller, S. R. & Skalak, R. 1982 Motion of a tank-treading ellipsoidal particle in a shear flow. J. Fluid Mech. 120, 27–47.Google Scholar
Kessler, S., Finken, R. & Seifert, U. 2008 Swinging and tumbling of elastic capsules in shear flow. J. Fluid Mech. 605, 207–226.Google Scholar
Khismatullin, D. B. & Truskey, G. A. 2012 Leukocyte rolling on p-selectin: a three-dimensional numerical study of the effect of cytoplasmic viscosity. Biophys. J. 102, 1757–1766.Google Scholar
Koleva, I. & Rehage, H. 2012 Deformation and orientation dynamics of polysiloxane microcapsules in linear shear flow. Soft Matt. 8, 3681–3693.Google Scholar
Koumoutsakos, P., Pivkin, I. & Milde, F. 2013 The fluid mechanics of cancer and its therapy. Annu. Rev. Fluid Mech. 45, 325–355.Google Scholar
Kwak, S. & Pozrikidis, C. 2001 Effect of membrane bending stiffness on the axisymmetric deformation of capsules in uniaxial extensional flow. Phys. Fluids 13, 1234–1242.Google Scholar
Lac, E. & Barthes-Biesel, D. 2005 Deformation of a capsule in simple shear flow: effect of membrane prestress. Phys. Fluids 17, 072105.Google Scholar
Lac, E., Barthes-Biesel, D., Pelekasis, N. A. & Tsamopoulos, J. 2004 Spherical capsules in three-dimensional unbounded stokes flows: effect of the membrane constitutive law and onset of buckling. J. Fluid Mech. 516, 303–334.Google Scholar
Le, D. V. 2010 Effect of bending stiffness on the deformation of liquid capsules enclosed by thin shells in shear flow. Phys. Rev. E 82, 016318.Google Scholar
Li, X. Y. & Sarkar, K. 2008 Front tracking simulation of deformation and buckling instability of a liquid capsule enclosed by an elastic membrane. J. Comput. Phys. 227, 4998–5018.Google Scholar
Luo, Z. Y. & Bai, B. F. 2016 Dynamics of nonspherical compound capsules in simple shear flow. Phys. Fluids 28, 101901.Google Scholar
Luo, Z. Y., He, L. & Bai, B. F. 2015 Deformation of spherical compound capsules in simple shear flow. J. Fluid Mech. 775, 77–104.Google Scholar
Luo, Z. Y., He, L., Wang, S. Q., Tasoglu, S., Xu, F., Demirci, U. & Bai, B. F. 2014 Two-dimensional numerical study of flow dynamics of a nucleated cell tethered under shear flow. Chem. Engng Sci. 119, 236–244.Google Scholar
Luo, Z. Y., Wang, S. Q., He, L., Xu, F. & Bai, B. F. 2013 Inertia-dependent dynamics of three-dimensional vesicles and red blood cells in shear flow. Soft Matt. 9, 9651–9660.Google Scholar
Matsunaga, D., Imai, Y., Yamaguchi, T. & Ishikawa, T. 2015 Deformation of a spherical capsule under oscillating shear flow. J. Fluid Mech. 762, 288–301.Google Scholar
Mukherjee, S. & Sarkar, K. 2009 Effects of viscosity ratio on deformation of a viscoelastic drop in a newtonian matrix under steady shear. J. Non-Newtonian Fluid Mech. 160, 104–112.Google Scholar
Ni, M. J., Komori, S. & Morley, N. 2003 Projection methods for the calculation of incompressible unsteady flows. Numer. Heat Transfer B-Fund. 44, 533–551.Google Scholar
Noble, P. F., Cayre, O. J., Alargova, R. G., Velev, O. D. & Paunov, V. N. 2004 Fabrication of ‘hairy’ colloidosomes with shells of polymeric microrods. J. Am. Chem. Soc. 126, 8092–8093.Google Scholar
Omori, T., Imai, Y., Yamaguchi, T. & Ishikawa, T. 2012 Reorientation of a nonspherical capsule in creeping shear flow. Phys. Rev. Lett. 108, 138102.Google Scholar
Popel, A. S. & Johnson, P. C. 2005 Microcirculation and hemorheology. Annu. Rev. Fluid Mech. 37, 43–69.Google Scholar
Pozrikidis, C. 2001 Effect of membrane bending stiffness on the deformation of capsules in simple shear flow. J. Fluid Mech. 440, 269–291.Google Scholar
Raffiee, A. H., Dabiri, S. & Ardekani, A. M. 2017 Deformation and buckling of microcapsules in a viscoelastic matrix. Phys. Rev. E 96, 032603.Google Scholar
Ramanujan, S. & Pozrikidis, C. 1998 Deformation of liquid capsules enclosed by elastic membranes in simple shear flow: large deformations and the effect of fluid viscosities. J. Fluid Mech. 361, 117–143.Google Scholar
Ramaswamy, S. & Leal, L. 1999 The deformation of a viscoelastic drop subjected to steady uniaxial extensional flow of a newtonian fluid. J. Non-Newtonian Fluid Mech. 85, 127–163.Google Scholar
Rożkiewicz, D. I., Myers, B. D. & Stupp, S. I. 2011 Interfacial self-assembly of cell-like filamentous microcapsules. Angew. Chem. Intl Ed. Engl. 50, 6324–6327.Google Scholar
Shrivastava, S. & Tang, J. 1993 Large deformation finite element analysis of non-linear viscoelastic membranes with reference to thermoforming. J. Strain Anal. Eng. 28, 31–51.Google Scholar
Skalak, R., Tozeren, A., Zarda, R. P. & Chien, S. 1973 Strain energy function of red blood cell membranes. Biophys. J. 13, 245–280.Google Scholar
Sui, Y., Chew, Y. T., Roy, P. & Low, H. T. 2009 Inertia effect on the transient deformation of elastic capsules in simple shear flow. Comput. Fluids 38, 49–59.Google Scholar
Taylor, G. I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A 146, 0501–0523.Google Scholar
Tryggvason, G., Bunner, B., Esmaeeli, A., Juric, D., Al-Rawahi, N., Tauber, W., Han, J., Nas, S. & Jan, Y. J. 2001 A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 169, 708–759.Google Scholar
Tsai, M. A., Frank, R. S. & Waugh, R. E. 1993 Passive mechanical behavior of human neutrophils: power-law fluid. Biophys. J. 65, 2078–2088.Google Scholar
Unverdi, S. O. & Tryggvason, G. 1992 A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 100, 25–37.Google Scholar
Verhulst, K., Cardinaels, R., Moldenaers, P., Afkhami, S. & Renardy, Y. 2009a Influence of viscoelasticity on drop deformation and orientation in shear flow. Part 2: dynamics. J. Non-Newtonian Fluid Mech. 156, 44–57.Google Scholar
Verhulst, K., Cardinaels, R., Moldenaers, P., Renardy, Y. & Afkhami, S. 2009b Influence of viscoelasticity on drop deformation and orientation in shear flow: part 1. Stationary states. J. Non-Newtonian Fluid Mech. 156, 29–43.Google Scholar
Villone, M. M., D’Avino, G., Hulsen, M. A. & Maffettone, P. L. 2015 Dynamics of prolate spheroidal elastic particles in confined shear flow. Phys. Rev. E 92, 062303.Google Scholar
Vlahovska, P. M., Young, Y. N., Danker, G. & Misbah, C. 2011 Dynamics of a non-spherical microcapsule with incompressible interface in shear flow. J. Fluid Mech. 678, 221–247.Google Scholar
Walter, J., Salsac, A. V. & Barthes-Biesel, D. 2011 Ellipsoidal capsules in simple shear flow: prolate versus oblate initial shapes. J. Fluid Mech. 676, 318–347.Google Scholar
Wang, Z., Sui, Y., Spelt, P. D. M. & Wang, W. 2013 Three-dimensional dynamics of oblate and prolate capsules in shear flow. Phys. Rev. E 88, 053021.Google Scholar
Yazdani, A. & Bagchi, P. 2011 Phase diagram and breathing dynamics of a single red blood cell and a biconcave capsule in dilute shear flow. Phys. Rev. E 84, 026314.Google Scholar
Yazdani, A. & Bagchi, P. 2012 Three-dimensional numerical simulation of vesicle dynamics using a front-tracking method. Phys. Rev. E 85, 056308.Google Scholar
Yazdani, A. & Bagchi, P. 2013 Influence of membrane viscosity on capsule dynamics in shear flow. J. Fluid Mech. 718, 569–595.Google Scholar
Yue, P., Feng, J. J., Liu, C. & Shen, J. 2005a Transient drop deformation upon startup of shear in viscoelastic fluids. Phys. Fluids 17, 123101.Google Scholar
Yue, P., Feng, J. J., Liu, C. & Shen, J. 2005b Viscoelastic effects on drop deformation in steady shear. J. Fluid Mech. 540, 427–437.Google Scholar
Zang, Y., Street, R. L. & Koseff, J. R. 1994 A non-staggered grid, fractional step method for time-dependent incompressible Navier–Stokes equations in curvilinear coordinates. J. Comput. Phys. 114, 18–33.Google Scholar
Zhang, Y., Yu, J., Bomba, H. N., Zhu, Y. & Gu, Z. 2016 Mechanical force-triggered drug delivery. Chem. Rev. 116, 12536–12563.Google Scholar
Zhao, M. Y. & Bagchi, P. 2011 Dynamics of microcapsules in oscillating shear flow. Phys. Fluids 23, 111901.Google Scholar