Article contents
Dynamics of a surface tension driven colloidal motor based on an active Janus particle encapsulated in a liquid drop
Published online by Cambridge University Press: 02 March 2023
Abstract
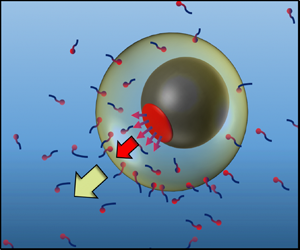
A colloidal motor driven by surface tension forces is theoretically designed by encapsulating an active Janus particle in a liquid drop which is immiscible in the suspending medium. The Janus particle produces an asymmetric flux of a solute species which induces surface tension gradients along the liquid–liquid interface between the drop and the surrounding fluid. The resulting Marangoni forces at the interface propel the compound drop/Janus particle system. The propulsion speeds of the motor are evaluated for a range of relative sizes and positions of the drop and the particle and across a range of transport properties of the drop and the suspending medium. It is demonstrated that the proposed design can produce higher propulsion velocities than the traditional Janus-particle-based colloidal motors propelled by neutral diffusiophoresis.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 5
- Cited by



