No CrossRef data available.
Article contents
Dynamics of a stratified vortex under the complete Coriolis force: two-dimensional three-components evolution
Published online by Cambridge University Press: 24 October 2022
Abstract
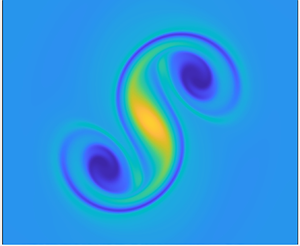
We study the dynamics of an initially axisymmetric and vertical Lamb–Oseen vortex in a stratified-rotating fluid under the complete Coriolis force on the 
$f$ plane, i.e. in the presence of a background rotation both along the vertical and horizontal directions. By a combination of direct numerical simulations and asymptotic analyses for small horizontal background rotation, we show that a critical layer appears at the radius where the angular velocity of the vortex is equal to the buoyancy frequency when the Froude number is larger than unity. This critical layer generates a vertical velocity that is invariant along the vertical and which first increases linearly with time and then saturates at an amplitude scaling like 
$Re^{1/3}/\widetilde{Ro}$, where 
$Re$ is the Reynolds number and 
$\widetilde {Ro}$ the non-traditional Rossby number based on the horizontal component of the background rotation. In turn, a quasi-axisymmetric anomaly of vertical vorticity is produced at the critical radius through the non-traditional Coriolis force. Below a critical 
$\widetilde {Ro}$ depending on 
$Re$, the Rayleigh's inflectional criterion is satisfied and a shear instability is subsequently triggered rendering the vertical vorticity fully non-axisymmetric. The decay of the angular velocity is then enhanced until it is everywhere lower than the buoyancy frequency. A theoretical criterion derived from the Rayleigh condition predicts well the instability. It shows that this phenomenon can occur even for a large non-traditional Rossby number 
$\widetilde {Ro}$ for large 
$Re$. Hence, the non-traditional Coriolis force might have much more impact on geophysical vortices than anticipated by considering the order of magnitude of 
$\widetilde {Ro}$.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
Abramowitz, M. & Stegun, I.A. (Ed.) 1972 Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th printing edn. US Government Printing Office.Google Scholar
Billant, P. & Bonnici, J. 2020 Evolution of a vortex in a strongly stratified shear flow. Part 2. Numerical simulations. J.Fluid Mech. 893, A18.CrossRefGoogle Scholar
Bonnici, J. 2018 Vertical decorrelation of a vortex by an external shear flow in a strongly stratified fluid. PhD thesis, Université Paris-Saclay.Google Scholar
Boulanger, N., Meunier, P. & Le Dizes, S. 2007 Structure of a stratified tilted vortex. J.Fluid Mech. 583, 443–458.CrossRefGoogle Scholar
Boulanger, N., Meunier, P. & Le Dizes, S. 2008 Tilt-induced instability of a stratified vortex. J.Fluid Mech. 596, 1–20.CrossRefGoogle Scholar
Carton, X. & Legras, B. 1994 The life-cycle of tripoles in two-dimensional incompressible flows. J.Fluid Mech. 267, 53–82.CrossRefGoogle Scholar
Deloncle, A., Billant, P. & Chomaz, J. 2008 Nonlinear evolution of the zigzag instability in stratified fluids: a shortcut on the route to dissipation. J.Fluid Mech. 599, 229–239.CrossRefGoogle Scholar
Etling, D. 1971 The stability of an Ekman boundary layer flow as influenced by thermal stratification. Beitr. Phys. Atmos. 44, 168–186.Google Scholar
Fjørtoft, R. 1950 Application of integral theorems in deriving criteria of stability for laminar flows and for the baroclinic circular vortex. Geophys. Publ. 17, 1–52.Google Scholar
Gerkema, T., Zimmerman, J.T.F., Maas, L.R.M. & Van Haren, H. 2008 Geophysical and astrophysical fluid dynamics beyond the traditional approximation. Rev. Geophys. 46, RG2004.CrossRefGoogle Scholar
Hayashi, M. & Itoh, H. 2012 The importance of the nontraditional Coriolis terms in large-scale motions in the tropics forced by prescribed cumulus heating. J.Atmos. Sci. 69 (9), 2699–2716.CrossRefGoogle Scholar
Igel, M.R. & Biello, J.A. 2020 The nontraditional Coriolis terms and tropical convective clouds. J.Atmos. Sci. 77 (12), 3985–3998.CrossRefGoogle Scholar
Kloosterziel, R.C., Carnevale, G.F. & Orlandi, P. 2017 Equatorial inertial instability with full Coriolis force. J.Fluid Mech. 825, 69–108.CrossRefGoogle Scholar
Kossin, J.P., Schubert, W.H. & Montgomery, M.T. 2000 Unstable interactions between a hurricane's primary eyewall and a secondary ring of enhanced vorticity. J.Atmos. Sci. 57 (24), 3893–3917.2.0.CO;2>CrossRefGoogle Scholar
Lavrovskii, E.K., Semenova, I.P., Slezkin, L.N. & Fominykh, V.V. 2000 Mediterranean lenses as liquid gyroscopes in the ocean. Dokl. Phys. 45 (11), 606–609.CrossRefGoogle Scholar
Park, J., Prat, V., Mathis, S. & Bugnet, L. 2021 Horizontal shear instabilities in rotating stellar radiation zones-II. Effects of the full Coriolis acceleration. Astron. Astrophys. 646, A64.CrossRefGoogle Scholar
Rayleigh, Lord 1880 On the stability, or instability, of certain fluid motions. Proc. Lond. Math. Soc. 9, 57–70.Google Scholar
Semenova, I.P. & Slezkin, L.N. 2003 Dynamically equilibrium shape of intrusive vortex formations in the ocean. Fluid Dyn. 38 (5), 663–669.CrossRefGoogle Scholar
Sheremet, V.A. 2004 Laboratory experiments with tilted convective plumes on a centrifuge: a finite angle between the buoyancy force and the axis of rotation. J.Fluid Mech. 506, 217–244.CrossRefGoogle Scholar
Tort, M. & Dubos, T. 2014 Dynamically consistent shallow-atmosphere equations with a complete Coriolis force. Q. J. R. Meteorol. Soc. 140 (684), 2388–2392.CrossRefGoogle Scholar
Tort, M., Dubos, T., Bouchut, F. & Zeitlin, V. 2014 Consistent shallow-water equations on the rotating sphere with complete Coriolis force and topography. J.Fluid Mech. 748, 789–821.CrossRefGoogle Scholar
Tort, M., Ribstein, B. & Zeitlin, V. 2016 Symmetric and asymmetric inertial instability of zonal jets on the-plane with complete Coriolis force. J.Fluid Mech. 788, 274–302.CrossRefGoogle Scholar
Wang, C. & Balmforth, N.J. 2020 Nonlinear dynamics of forced baroclinic critical layers. J.Fluid Mech. 883, A12.CrossRefGoogle Scholar
Wang, C. & Balmforth, N.J. 2021 Nonlinear dynamics of forced baroclinic critical layers II. J.Fluid Mech. 917, A48.CrossRefGoogle Scholar
Wippermann, F. 1969 The orientation of vortices due to instability of the Ekman-boundary layer. Beitr. Phys. Atmos. 42 (4), 225–244.Google Scholar
Zeitlin, V. 2018 Symmetric instability drastically changes upon inclusion of the full Coriolis force. Phys. Fluids 30 (6), 061701.CrossRefGoogle Scholar
Toghraei and Billant supplementary movie 1
Evolution of the vertical velocity (left) and vertical vorticity (right) for $Re=2000$, $F_h=10$, $Ro=23.1$, $\phi=60^{\circ}$ ($\widetilde{Ro}=40$).
Video
2.8 MB
Toghraei and Billant supplementary movie 2
Evolution of the vertical velocity (left) and vertical vorticity (right) for $Re=2000$, $F_h=2$, $Ro=23.1$, $\phi=60^{\circ}$ ($\widetilde{Ro}=40$).
Video
1.9 MB
Toghraei and Billant supplementary movie 3
Evolution of the vertical velocity (left) and vertical vorticity (right) for $Re=2000$, $F_h=2$, $Ro=20.3$, $\phi=80^{\circ}$ ($\widetilde{Ro}=115.2$).
Video
1.4 MB
Toghraei and Billant supplementary movie 4
Evolution of the vertical velocity (left) and vertical vorticity (right) for $Re=10000$, $F_h=2$, $Ro=20.3$, $\phi=80^{\circ}$ ($\widetilde{Ro}=115.5$).
Video
2.2 MB