Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T04:59:15.649Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics and excitation in a low mass-damping cylinder in cross-flow with side-by-side interference

Published online by Cambridge University Press:  04 July 2018

Francisco J. Huera-Huarte Open the ORCID record for Francisco J. Huera-Huarte [Opens in a new window]
Francisco J. Huera-Huarte*
Affiliation:
Department of Mechanical Engineering, Universitat Rovira i Virgili (URV), 43007 Tarragona, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Experiments have been conducted with a low mass-damping circular cylinder, elastically supported in a cross-flow, in the vicinity of a second stationary cylinder. The dynamic response, including amplitudes and frequencies of oscillation, together with the fluid excitation, were measured covering a large parametric space, consisting of variations in the gap distance between the cylinders as well as in the reduced velocity and Reynolds number. The flow dynamics in the near wake was also measured using planar particle image velocimetry. 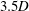The results show how there is a strong wake interaction between the cylinders that greatly modifies the vortex-induced vibrations (VIV) of the elastically mounted cylinder when the centre-to-centre distance between the models is initially set to values smaller than $3.5D$, where 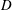$D$ is the external diameter. The wake interference leads to responding amplitudes that are reduced if compared to those of isolated cylinders undergoing VIV, while responding frequencies are increased. The transverse force coefficients observed in the lock-in region increase and the upper branch shifts to smaller reduced velocities. The phase between motion and excitation is also shifted and values measured in the lower branch of the response tend to be smaller than those typical of isolated cylinders. At the smallest separation distances investigated, the wakes of the cylinders are synchronised in an out-of-phase mode of shedding, characterised by a biased flow towards the oscillating cylinder.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 370 - 400
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. M. & Sakamoto, H. 2005 Investigation of Strouhal frequencies of two staggered bluff bodies and detection of multistable flow by wavelets. J. Fluids Struct. 20 (3), 425–449.Google Scholar
Alam, M. M. & Zhou, Y. 2007 Flow around two side-by-side closely spaced circular cylinders. J. Fluids Struct. 23 (5), 799–805.Google Scholar
Anagnostopoulos, P. & Bearman, P. W. 1992 Response characteristics of a vortex-excited cylinder at low Reynolds numbers. J. Fluids Struct. 6 (1), 39–50.Google Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.Google Scholar
Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27 (5–6), 648–658.Google Scholar
Bearman, P. W. & Wadcock, A. J. 1973 The interaction between a pair of circular cylinders normal to a stream. J. Fluid Mech. 61 (03), 499–511.Google Scholar
Blevins, R. D. 1990 Flow-Induced Vibration, 2nd edn. Van Nostrand Reinhold.Google Scholar
Brankovic, M.2004 Vortex-induced vibration attenuation of circular cylinders with low mass and damping. PhD thesis, Imperial College London.Google Scholar
Chaplin, J. R., Bearman, P. W., Huera-Huarte, F. J. & Pattenden, R. J. 2005 Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current. J. Fluids Struct. 21 (1), 3–24.Google Scholar
Huera-Huarte, F. J. 2017 Suppression of vortex-induced vibration in low mass-damping circular cylinders using wire meshes. Mar. Struct. 55, 200–213.Google Scholar
Huera-Huarte, F. J. & Gharib, M. 2011 Flow-induced vibrations of a side-by-side arrangement of two flexible circular cylinders. J. Fluids Struct. 27 (3), 354–366.Google Scholar
Huera-Huarte, F. J. & Bearman, P. W. 2009 Wake structures and vortex-induced vibrations of a long flexible cylinder – Part 1: dynamic response. J. Fluids Struct. 25 (6), 969–990.Google Scholar
Jiménez-González, J. I. & Huera-Huarte, F. J. 2017 Experimental sensitivity of vortex-induced vibrations to localized wake perturbations. J. Fluids Struct. 74, 53–63.Google Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7–8), 813–851.Google Scholar
Kim, H. J. & Durbin, P. A. 1988 Investigation of the flow between a pair of circular cylinders in the flopping regime. J. Fluid Mech. 196, 431–448.Google Scholar
Li, Z., Yao, W., Yang, K., Jaiman, R. K. & Khoo, B. C. 2016 On the vortex-induced oscillations of a freely vibrating cylinder in the vicinity of a stationary plane wall. J. Fluids Struct. 65, 495–526.Google Scholar
Liu, B. & Jaiman, R. K. 2016 Interaction dynamics of gap flow with vortex-induced vibration in side-by-side cylinder arrangement. Phys. Fluids 28 (12), 127103.Google Scholar
Liu, B. & Jaiman, R. K.2018 Dynamics of gap flow interference in a vibrating side-by-side arrangement of two circular cylinders at moderate Reynolds number. arXiv:1801.05109 [physics.flu-dyn].Google Scholar
Païdoussis, M. P., Price, S. J. & De Langre, E. 2010 Fluid-structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Panter, P. F. 1965 Modulation, Noise, and Spectral Analysis: Applied to Information Tranmission. McGraw-Hill.Google Scholar
Peschard, I. & Le Gal, P. 1996 Coupled wakes of cylinders. Phys. Rev. Lett. 77 (15), 3122–3125.Google Scholar
Rosenblum, M., Pikovsky, A. & Kurths, J. 1997 Phase synchronization in noisy and chaotic oscillators. In Stochastic Dynamics (ed. Schimansky-Geier, L. & Pöschel, T.), Lecture Notes in Physics, vol 484. Springer.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19, 389–447.Google Scholar
Seyed-aghazadeh, B. & Carlson, D. W. 2017 Vortex-induced vibration and galloping of prisms with triangular cross-sections. J. Fluid Mech. 817, 590–618.Google Scholar
Seyed-Aghazadeh, B., Carlson, D. W. & Modarres-Sadeghi, Y. 2015 The influence of taper ratio on vortex-induced vibration of tapered cylinders in the crossflow direction. J. Fluids Struct. 53, 84–95.Google Scholar
Sumer, B. M. & Fredsoe, J. 1997 Hydrodynamics Around Cylindrical Structures, 2nd edn. World Scientific.Google Scholar
Sumner, D. 2010 Two circular cylinders in cross-flow: a review. J. Fluids Struct. 26 (6), 849–899.Google Scholar
Sumner, D., Wong, S. S. T., Price, S. J. & Païdoussis, M. P. 1999 Fluid behaviour of side-by-side circular cylinders in steady cross-flow. J. Fluids Struct. 13 (3), 309–338.Google Scholar
Tham, D. M. Y., Gurugubelli, P. S., Li, Z. & Jaiman, R. K. 2015 Freely vibrating circular cylinder in the vicinity of a stationary wall. J. Fluids Struct. 59, 103–128.Google Scholar
Wei, C. Y. & Chang, J. R. 2002 Wake and base-bleed flow downstream of bluff bodies with different geometry. Exp. Therm. Fluid Sci. 26 (1), 39–52.Google Scholar
Willert, C. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10, 181–193.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Yildirim, I., Rindt, C. C. M. & Steenhoven, A. A. 2010 Vortex dynamics in a wire-disturbed cylinder wake. Phys. Fluids 22 (9), 1–15.Google Scholar
Zdravkovich, M. M. 1997 Flow Around Cylindrical Structures, vol. 2: Applications, 1st edn. Oxford University Press.Google Scholar
Zhou, Y., Wang, Z. J., So, R. M. C., Xu, S. J. & Jin, W. 2001 Free vibrations of two side-by-side cylinders in a cross-flow. J. Fluid Mech. 443, 197–229.Google Scholar