Article contents
Dynamical effect of the total strain induced by the coherent motion on local isotropy in a wake
Published online by Cambridge University Press: 27 February 2013
Abstract
We assess the extent to which local isotropy (LI) holds in a wake flow for different initial conditions, which may be geometrical (the shape of the bluff body which creates the wake) and hydrodynamical (the Reynolds number), as a function of the dynamical effects of the large-scale forcing (the mean strain, 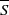 $ \overline{S} $, combined with the strain induced by the coherent motion,
$ \overline{S} $, combined with the strain induced by the coherent motion, 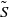 $\tilde {S} $). LI is appraised through either classical kinematic tests or phenomenological approaches. In this respect, we reanalyse existing LI criteria and formulate a new isotropy criterion based on the ratio between the turbulence strain intensity and the total strain (
$\tilde {S} $). LI is appraised through either classical kinematic tests or phenomenological approaches. In this respect, we reanalyse existing LI criteria and formulate a new isotropy criterion based on the ratio between the turbulence strain intensity and the total strain (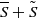 $ \overline{S} + \tilde {S} $). These criteria involve either time-averaged or phase-averaged quantities, thus providing a deeper insight into the dynamical aspect of these flows. They are tested using hot wire data in the intermediate wake of five types of obstacles (a circular cylinder, a square cylinder, a screen cylinder, a normal plate and a screen strip). We show that in the presence of an organized motion, isotropy is not an adequate assumption for the large scales but may be satisfied over a range of scales extending from the smallest dissipative scale up to a scale which depends on the total strain rate that characterizes the flow. The local value of this scale depends on the particular nature of the wake and the phase of the coherent motion. The square cylinder wake is the closest to isotropy whereas the least locally isotropic flow is the screen strip wake. For locations away from the axis, the study is restricted to the circular cylinder only and reveals that LI holds at scales smaller than those that apply at the wake centreline. Arguments based on self-similarity show that in the far wake, the strength of the coherent motion decays at the same rate as that of the turbulent motion. This implies the persistence of the same degree of anisotropy far downstream, independently of the scale at which anisotropy is tested.
$ \overline{S} + \tilde {S} $). These criteria involve either time-averaged or phase-averaged quantities, thus providing a deeper insight into the dynamical aspect of these flows. They are tested using hot wire data in the intermediate wake of five types of obstacles (a circular cylinder, a square cylinder, a screen cylinder, a normal plate and a screen strip). We show that in the presence of an organized motion, isotropy is not an adequate assumption for the large scales but may be satisfied over a range of scales extending from the smallest dissipative scale up to a scale which depends on the total strain rate that characterizes the flow. The local value of this scale depends on the particular nature of the wake and the phase of the coherent motion. The square cylinder wake is the closest to isotropy whereas the least locally isotropic flow is the screen strip wake. For locations away from the axis, the study is restricted to the circular cylinder only and reveals that LI holds at scales smaller than those that apply at the wake centreline. Arguments based on self-similarity show that in the far wake, the strength of the coherent motion decays at the same rate as that of the turbulent motion. This implies the persistence of the same degree of anisotropy far downstream, independently of the scale at which anisotropy is tested.
JFM classification
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 23
- Cited by


