Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Gao-Jin
and
Lu, Xi-Yun
2012.
Force and power of flapping plates in a fluid.
Journal of Fluid Mechanics,
Vol. 712,
Issue. ,
p.
598.
Dai, Hu
Luo, Haoxiang
de Sousa, Paulo J. S. A. Ferreira
and
Doyle, James F.
2012.
Thrust performance of a flexible low-aspect-ratio pitching plate.
Physics of Fluids,
Vol. 24,
Issue. 10,
Erzincanli, Belkis
and
Sahin, Mehmet
2013.
An arbitrary Lagrangian–Eulerian formulation for solving moving boundary problems with large displacements and rotations.
Journal of Computational Physics,
Vol. 255,
Issue. ,
p.
660.
Peng, Diing-wen
and
Milano, Michele
2013.
Lift generation with optimal elastic pitching for a flapping plate.
Journal of Fluid Mechanics,
Vol. 717,
Issue. ,
Zheng, Lingxiao
Hedrick, Tyson L.
Mittal, Rajat
and
Aegerter, Christof Markus
2013.
Time-Varying Wing-Twist Improves Aerodynamic Efficiency of Forward Flight in Butterflies.
PLoS ONE,
Vol. 8,
Issue. 1,
p.
e53060.
Zheng, L
Hedrick, T
and
Mittal, R
2013.
A comparative study of the hovering efficiency of flapping and revolving wings.
Bioinspiration & Biomimetics,
Vol. 8,
Issue. 3,
p.
036001.
Tian, Fang-Bao
Luo, Haoxiang
Song, Jialei
and
Lu, Xi-Yun
2013.
Force production and asymmetric deformation of a flexible flapping wing in forward flight.
Journal of Fluids and Structures,
Vol. 36,
Issue. ,
p.
149.
Deng, Hong-Bin
Xu, Yuan-Qing
Chen, Duan-Duan
Dai, Hu
Wu, Jian
and
Tian, Fang-Bao
2013.
On numerical modeling of animal swimming and flight.
Computational Mechanics,
Vol. 52,
Issue. 6,
p.
1221.
Ha, Ngoc San
Truong, Quang Tri
Goo, Nam Seo
and
Park, Hoon Cheol
2013.
Relationship between wingbeat frequency and resonant frequency of the wing in insects.
Bioinspiration & Biomimetics,
Vol. 8,
Issue. 4,
p.
046008.
Mattheijssens, Joris
Marcel, Jean-Paul
Bosschaerts, Walter
and
Lefeber, Dirk
2013.
Performance of heaving and passively pitching hydrofoils.
Zheng, Lingxiao
Hedrick, Tyson L.
and
Mittal, Rajat
2013.
A multi-fidelity modelling approach for evaluation and optimization of wing stroke aerodynamics in flapping flight.
Journal of Fluid Mechanics,
Vol. 721,
Issue. ,
p.
118.
Luo, Haoxiang
Dai, Hu
Song, Jialei
and
Doyle, James
2013.
Effect of pre-existing camber on fluid--structure interaction of cicada wings.
Yin, Bo
and
Luo, Haoxiang
2013.
Hydrodynamic interaction of oblique sheets in tandem arrangement.
Physics of Fluids,
Vol. 25,
Issue. 1,
Ishihara, D
Horie, T
and
Niho, T
2014.
An experimental and three-dimensional computational study on the aerodynamic contribution to the passive pitching motion of flapping wings in hovering flies.
Bioinspiration & Biomimetics,
Vol. 9,
Issue. 4,
p.
046009.
Zhu, Xiaojue
He, Guowei
and
Zhang, Xing
2014.
Numerical study on hydrodynamic effect of flexibility in a self-propelled plunging foil.
Computers & Fluids,
Vol. 97,
Issue. ,
p.
1.
Song, Jialei
Luo, Haoxiang
and
Hedrick, Tyson L.
2014.
Three-dimensional flow and lift characteristics of a hovering ruby-throated hummingbird.
Journal of The Royal Society Interface,
Vol. 11,
Issue. 98,
Qi, Dewei
He, Guowei
and
Liu, Yingming
2014.
Lattice Boltzmann simulations of a pitch-up and pitch-down maneuver of a chord-wise flexible wing in a free stream flow.
Physics of Fluids,
Vol. 26,
Issue. 2,
Hua, Ru-Nan
Zhu, Luoding
and
Lu, Xi-Yun
2014.
Dynamics of fluid flow over a circular flexible plate.
Journal of Fluid Mechanics,
Vol. 759,
Issue. ,
p.
56.
Moore, M. Nicholas J.
2014.
Analytical results on the role of flexibility in flapping propulsion.
Journal of Fluid Mechanics,
Vol. 757,
Issue. ,
p.
599.
Sotiropoulos, Fotis
and
Yang, Xiaolei
2014.
Immersed boundary methods for simulating fluid–structure interaction.
Progress in Aerospace Sciences,
Vol. 65,
Issue. ,
p.
1.
 , and natural frequency of the wing,
, and natural frequency of the wing, 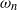 , as the non-dimensional stiffness. In general, when
, as the non-dimensional stiffness. In general, when 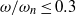 , the deformation significantly enhances the lift and also improves the lift efficiency despite a disadvantageous camber. In particular, when the inertial pitching torque is assisted by an aerodynamic torque of comparable magnitude, the lift efficiency can be markedly improved.
, the deformation significantly enhances the lift and also improves the lift efficiency despite a disadvantageous camber. In particular, when the inertial pitching torque is assisted by an aerodynamic torque of comparable magnitude, the lift efficiency can be markedly improved.

