Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-20T17:26:26.155Z Has data issue: false hasContentIssue false
  • English
  • Français

Drop motion through a confining orifice

Published online by Cambridge University Press:  28 October 2014

Ankur D. Bordoloi  and
Ellen K. Longmire
Ankur D. Bordoloi*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Ellen K. Longmire
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

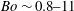The motion of gravity-driven deformable drops (Bond number, $\mathit{Bo}\sim 0.8{-}11$) through a circular confining orifice (ratio of orifice diameter to drop diameter, 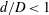$d/D<1$) was studied using high-speed imaging. Drops of water/glycerin, surrounded by silicone oil, fall toward and encounter the orifice plate after reaching terminal speed. The effects of surface wettability were investigated for both round-edged and sharp-edged orifices. For the round-edged case, a thin film of surrounding oil prevents the drop fluid from contacting the orifice surface, such that the flow outcomes of the drops are independent of surface wettability. For 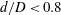$d/D<0.8$, the boundary between drop capture and release depends on a modified Bond number relating drop gravitational time scale to orifice surface tension time scale and is independent of viscosity ratio. Drops that release break into multiple fragments for larger 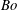$\mathit{Bo}$ and smaller 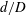$d/D$. For the sharp-edged case, a contact is initiated at the orifice edge immediately upon impact, such that surface wettability influences the drop outcome. When the surface is hydrophobic, the contact line motion through the orifice enhances penetration of the drop fluid, but the trailing interface becomes pinned at the orifice edge, inhibiting drop release. When the surface is hydrophilic, a fraction of the drop fluid is always captured because the drop fluid spreads on both the upper and lower plate surfaces.

JFM classification

Drops and Bubbles: Breakup/coalescence Interfacial Flows (free surface): Contact lines Drops and Bubbles: Drops
Type
Papers
Information
Journal of Fluid Mechanics , Volume 759 , 25 November 2014 , pp. 520 - 545
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bird, J. C., Mandre, S. & Stone, H. 2008 Short-time dynamics of partial wetting. Phys. Rev. Lett. 100, 234501.Google Scholar
Bogy, D. B. 1979 Drop formation in a circular liquid jet. Annu. Rev. Fluid Mech. 11, 207–228.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739–805.Google Scholar
Cachile, M., Chertcoff, R., Calvo, A., Rosen, M., Hulin, J. P. & Cazabat, A. M. 1996 Residual film dynamics in glass capillaries. J. Colloid Interface Sci. 182, 483–491.Google Scholar
Chen, X., Mandre, S. & Feng, J. 2006 Partial coalescence between a drop and a liquid–liquid interface. Phys. Fluids 18, 051705.Google Scholar
Clanet, C., Béguin, C., Richard, D. & Quéré, D. 2004 Maximal deformation of an impacting drop. J. Fluid Mech. 517, 199–208.CrossRefGoogle Scholar
Clarke, A., Blake, T. D., Carruthers, K. & Woodward, A. 2002 Spreading and imbibition of liquid droplets on porous surfaces. Langmuir 18, 2980–2984.CrossRefGoogle Scholar
Courbin, L., Bird, J. C., Reyssat, M. & Stone, H. 2009 Dynamics of wetting: from inertial spreading to viscous imbibition. J. Phys. Condens. Matter 21, 464127.CrossRefGoogle ScholarPubMed
Delbos, A., Lorenceau, E. & Pitois, O. 2010 Forced impregnation of a capillary tube with drop impact. J. Colloid Interface Sci. 341, 171–177.Google Scholar
Denesuk, M., Smoth, G. L., Zelinski, B. J. J., Kreidl, N. J. & Uhlmann, D. R. 1993 Capillary penetration of liquid droplets into porous materials. J. Colloid Interface Sci. 158, 114–120.Google Scholar
Ding, H. & Theofanous, T. G. 2012 The inertial regime of drop impact on an anisotropic porous substrate. J. Fluid Mech. 691, 546–567.Google Scholar
Guido, S. & Preziosi, V. 2010 Droplet deformation under confined Poiseuille flow. J. Colloid Interface Sci. 161, 89–101.CrossRefGoogle ScholarPubMed
Herminghaus, S., Brinkmann, M. & Seemann, R. 2008 Wetting and dewetting of complex surface geometries. Annu. Rev. Fluid Mech. 38, 101–121.Google Scholar
Longmire, E. K., Norman, T. L. & Gefroh, D. L. 2001 Dynamics of pinch-off in liquid/liquid jets with surface tension. Intl J. Multiphase Flow 27, 1735–1752.Google Scholar
Lorenceau, É. & Quéré, D. 2003 Drops impacting a sieve. J. Colloid Interface Sci. 263, 244–249.Google Scholar
Mohamed-Kassim, Z. & Longmire, E. K. 2003 Drop impact on a liquid/liquid interface. Phys. Fluids 15, 3263–3273.Google Scholar
Mohamed-Kassim, Z. & Longmire, E. K. 2004 Drop coalescence through a liquid/liquid interface. Phys. Fluids 16, 2170–2181.CrossRefGoogle Scholar
Olbricht, W. L. 1996 Pore-scale prototypes of multiphase flow in porous media. Annu. Rev. Fluid Mech. 28, 187–213.Google Scholar
Protiére, S., Bazant, M. Z., Weitz, D. A. & Stone, H. A. 2010 Droplet breakup in flow past an obstacle: a capillary instability due to permeability variations. Europhys. Lett. 92, 54002, 1–6.Google Scholar
Ratcliffe, T., Zinchenko, A. Z. & Davis, R. 2010 Buoyancy-induced squeezing of a deformable drop through an axisymmetric ring constriction. Phys. Fluids 22, 082101.Google Scholar
Ratcliffe, T., Zinchenko, A. Z. & Davis, R. 2012 Simulations of gravity-induced trapping of a deformable drop in a three-dimensional constriction. J. Colloid Interface Sci. 383, 167–176.Google Scholar
Richard, D. & Quéré, D. 2000 Bouncing water drops. Europhys. Lett. 50, 769–775.CrossRefGoogle Scholar
Snoeijer, J. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.CrossRefGoogle Scholar
Steinhaus, B., Spicer, P. T. & Shen, A. Q. 2006 Droplet size effects on film drainage between droplet and substrate. Langmuir 22, 5308–5313.Google Scholar
Tsai, T. M. & Miksis, M. J. 1994 Dynamics of drop in a constricted capillary tube. J. Fluid Mech. 274, 197–217.Google Scholar
Zinchenko, A. Z. & Davis, R. 2006 A boundary-integral study of a drop squeezing through interparticle constrictions. J. Fluid Mech. 564, 227–266.Google Scholar