Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T04:12:00.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Drawing of micro-structured fibres: circular and non-circular tubes

Published online by Cambridge University Press:  14 August 2014

Yvonne M. Stokes ,
Peter Buchak ,
Darren G. Crowdy  and
Heike Ebendorff-Heidepriem
Yvonne M. Stokes*
Affiliation:
School of Mathematical Sciences, The University of Adelaide, North Terrace, Adelaide, SA 5005, Australia
Peter Buchak
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK
Darren G. Crowdy
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK
Heike Ebendorff-Heidepriem
Affiliation:
Institute for Photonics and Advanced Sensing, School of Chemistry and Physics, The University of Adelaide, North Terrace, Adelaide, SA 5005, Australia
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A general mathematical framework is presented for modelling the pulling of optical glass fibres in a draw tower. The only modelling assumption is that the fibres are slender; cross-sections along the fibre can have general shape, including the possibility of multiple holes or channels. A key result is to demonstrate how a so-called reduced time variable $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\tau $ serves as a natural parameter in describing how an axial-stretching problem interacts with the evolution of a general surface-tension-driven transverse flow via a single important function of $\tau $, herein denoted by 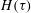$H(\tau )$, derived from the total rescaled cross-plane perimeter. For any given preform geometry, this function 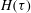$H(\tau )$ may be used to calculate the tension required to produce a given fibre geometry, assuming only that the surface tension is known. Of principal practical interest in applications is the ‘inverse problem’ of determining the initial cross-sectional geometry, and experimental draw parameters, necessary to draw a desired final cross-section. Two case studies involving annular tubes are presented in detail: one involves a cross-section comprising an annular concatenation of sintering near-circular discs, the cross-section of the other is a concentric annulus. These two examples allow us to exemplify and explore two features of the general inverse problem. One is the question of the uniqueness of solutions for a given set of experimental parameters, the other concerns the inherent ill-posedness of the inverse problem. Based on these examples we also give an experimental validation of the general model and discuss some experimental matters, such as buckling and stability. The ramifications for modelling the drawing of fibres with more complicated geometries, and multiple channels, are discussed.

JFM classification

Interfacial Flows (free surface): Capillary flows Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Lubrication theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 755 , 25 September 2014 , pp. 176 - 203
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© 2014 Cambridge University Press

References

Boyd, K., Ebendorff-Heidepriem, H., Monro, T. M. & Munch, J. 2012 Surface tension and viscosity measurement of optical glasses using a scanning $\mathrm{CO}_2$ laser. Opt. Mater. Express 2 (8), 1101–1110.Google Scholar
Buchak, P., Crowdy, D. G. & Stokes, Y. 2014 Elliptical pore regularization of the inverse problem for microstructured optical fibre fabrication. J. Fluid Mech. (submitted).Google Scholar
Chen, Y. & Birks, T. A. 2013 Predicting hole sizes after fibre drawing without knowing the viscosity. Opt. Mater. Express 3 (3), 346–356.Google Scholar
Crowdy, D. G. 2003 Viscous sintering of unimodal and bimodal cylindrical packings with shrinking pores. Eur. J. Appl. Maths 14, 421–445.Google Scholar
Crowdy, D. G. & Tanveer, S. 1998a A theory of exact solutions for plane viscous blobs. J. Nonlinear Sci. 8 (3), 261–279.CrossRefGoogle Scholar
Crowdy, D. G. & Tanveer, S. 1998b A theory of exact solutions for annular viscous blobs. J. Nonlinear Sci. 8 (4), 375–400.Google Scholar
Cummings, L. J. & Howell, P. D. 1999 On the evolution of non-axisymmetric viscous fibres with surface tension, inertia and gravity. J. Fluid Mech. 389, 361–389.CrossRefGoogle Scholar
Cummings, L. J., Howison, S. D. & King, J. R. 1997 Conserved quantities in Stokes flow with free surfaces. Phys. Fluids 9, 477–480.Google Scholar
Denn, M. M. 1980 Continuous drawing of liquids to form fibres. Annu. Rev. Fluid Mech. 12, 365–387.CrossRefGoogle Scholar
DeWynne, J. N., Howell, P. D. & Wilmott, P. 1994 Slender viscous fibres with inertia and gravity. Q. J. Mech. Appl. Maths 47, 541–555.Google Scholar
Fitt, A. D., Furusawa, K., Monro, T. M., Please, C. P. & Richardson, D. A. 2002 The mathematical modelling of capillary drawing for holey fibre manufacture. J. Engng Maths 43, 201–227.Google Scholar
Gospodinov, P. & Yarin, A. L. 1997 Draw resonance of optical microcapillaries in non-isothermal drawing. Intl J. Multiphase Flow 23, 967–976.CrossRefGoogle Scholar
Griffiths, I. M. & Howell, P. D. 2007 The surface-tension-driven evolution of a two-dimensional annular viscous tube. J. Fluid Mech. 593, 181–208.Google Scholar
Griffiths, I. M. & Howell, P. D. 2008 Mathematical modelling of non-axisymmetric capillary tube drawing. J. Fluid Mech. 605, 181–206.CrossRefGoogle Scholar
Griffiths, I. M. & Howell, P. D. 2009 The surface-tension-driven retraction of a viscida. SIAM J. Appl. Maths 70 (5), 1453–1487.Google Scholar
Hopper, R. W. 1990 Plane Stokes flow driven by capillarity on a free surface. J. Fluid Mech. 213, 349–375.Google Scholar
Howell, P. D.1994 Extensional thin layer flows. PhD thesis, University of Oxford.Google Scholar
Kaye, A. 1990 Convected coordinates and elongational flow. J. Non-Newtonian Fluid Mech. 40, 55–77.Google Scholar
Knight, J. C. 2003 Photonic crystal fibres. Nature 424, 847–851.Google Scholar
Kostecki, R., Ebendorff-Heidepriem, H., Warren-Smith, S. C. & Monro, T. M. 2014 Predicting the drawing conditions for microstructured optical fibre fabrication. Opt. Mater. Express 4, 29–40.Google Scholar
Langlois, W. 1964 Slow Viscous Flows. Macmillan.Google Scholar
Matovich, M. A. & Pearson, J. R. A. 1969 Spinning a molten threadline. Ind. Engng Chem. Fundam. 8, 512–520.Google Scholar
Monro, T. M. & Ebendorff-Heidepriem, H. 2006 Progress in microstructured optical fibres. Annu. Rev. Mater. Res. 36, 467–495.Google Scholar
Muskhelishvili, N. I. 1977 Some Basic Problems in the Mathematical Theory of Elasticity. Springer.Google Scholar
Pearson, J. R. A. & Matovich, M. A. 1969 Spinning a molten threadline; stability. Ind. Engng Chem. Fundam. 8, 605–609.Google Scholar
Richardson, S. 1992 Two-dimensional slow viscous flows with time dependent free boundaries driven by surface tension. Eur. J. Appl. Maths 3, 198–207.Google Scholar
Richardson, S. 2000 Plane Stokes flow with time-dependent free boundaries in which the fluid occupies a doubly connected region. Eur. J. Appl. Maths 11, 249–269.CrossRefGoogle Scholar
Scheid, B., Quiligotti, S., Tranh, B., Gy, R. & Stone, H. A. 2010 On the (de)stabilization of draw resonance due to cooling. J. Fluid Mech. 636, 155–176.Google Scholar
Stokes, Y. M., Tuck, E. O. & Schwartz, L. W. 2000 Extensional fall of a very viscous fluid drop. Q. J. Mech. Appl. Maths 53, 565–582.Google Scholar
Taroni, M., Breward, C. J. W., Cummings, L. J. & Griffiths, I. M. 2013 Asymptotic solutions of glass temperature profiles during steady optical fibre drawing. J. Engng Maths 80, 1–20.Google Scholar
Tchavdarov, B., Yarin, A. L. & Radev, S. 1993 Buckling of thin liquid jets. J. Fluid Mech. 253, 593–615.Google Scholar
van de Vorst, G. A. L. & Mattheij, R. M. M. 1995 A BEM-BDF scheme for curvature driven moving Stokes flows. J. Comput. Phys. 120, 1–14.Google Scholar
Voyce, C. J., Fitt, A. D. & Monro, T. M. 2004 Mathematical model of the spinning of microstructured fibres. Opt. Express 12 (23), 5810–5820.Google Scholar
Voyce, C. J., Fitt, A. D. & Monro, T. M. 2008 The mathematical modelling of rotating capillary tubes for holey-fibre manufacture. J. Engng Maths 60, 69–87.Google Scholar
Wilson, S. D. R. 1988 The slow dripping of a viscous fluid. J. Fluid Mech. 190, 561–570.Google Scholar
Wylie, J. J., Huang, H. & Miura, R. M. 2007 Thermal instability in drawing viscous threads. J. Fluid Mech. 570, 1–16.Google Scholar
Xue, S. C., Large, M. C. J., Barton, G. W., Tanner, R. I., Poladian, L. & Lwin, R. 2005a Role of material properties and drawing conditions in the fabrication of microstructured optical fibres. J. Lightwave Technol. 24, 853–860.CrossRefGoogle Scholar
Xue, S. C., Tanner, R. I., Barton, G. W., Lwin, R., Large, M. C. J. & Poladian, L. 2005b Fabrication of microstructured optical fibres – part I: problem formulation and numerical modelling of transient draw process. J. Lightwave Technol. 23, 2245–2254.Google Scholar
Xue, S. C., Tanner, R. I., Barton, G. W., Lwin, R., Large, M. C. J. & Poladian, L. 2005c Fabrication of microstructured optical fibres – part II: numerical modelling of steady-state draw process. J. Lightwave Technol. 23, 2255–2266.Google Scholar
Yarin, A. L. 1993 Free Liquid Jets and Films: Hydrodynamics and Rheology. Longman Scientific & Technical and Wiley & Sons.Google Scholar
Yarin, A. L. 1995 Surface-tension-driven flows at low Reynolds number arising in optoelectronic technology. J. Fluid Mech. 286, 173–200.CrossRefGoogle Scholar
Yarin, A. L., Gospodinov, P. & Roussinov, V. I. 1994 Stability loss and sensitivity in hollow fibre drawing. Phys. Fluids 6, 1454–1463.Google Scholar
Yarin, A., Rusinov, V. I., Gospodinov, P. & Radev, St. 1989 Quasi one-dimensional model of drawing of glass micro capillaries and approximate solutions. Theor. Appl. Mech. 20 (3), 55–62.Google Scholar