Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T16:56:55.732Z Has data issue: false hasContentIssue false
  • English
  • Français

Drag reduction and instabilities of flows in longitudinally grooved annuli

Published online by Cambridge University Press:  19 February 2019

H. V. Moradi Open the ORCID record for H. V. Moradi [Opens in a new window]  and
J. M. Floryan Open the ORCID record for J. M. Floryan [Opens in a new window]
H. V. Moradi*
Affiliation:
Department of Mechanical and Materials Engineering, Western University, London, Ontario, N6A 5B9, Canada
J. M. Floryan
Affiliation:
Department of Mechanical and Materials Engineering, Western University, London, Ontario, N6A 5B9, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The primary and secondary laminar flows in annuli with longitudinal grooves and driven by pressure gradients have been analysed. There exist geometric configurations reducing pressure losses in primary flows in spite of an increase of the wall wetted area. The parameter ranges when such flows exist have been determined using linear stability theory. Two types of secondary flows have been identified. The first type has the form of the classical travelling waves driven by shear and modified by the grooves. The axisymmetric waves dominate for sufficiently large radii of the annuli while different spiral waves dominate for small radii. The secondary flow topology is unique in the former case and has the form of axisymmetric rings propagating in the axial direction. Topologies in the latter case are not unique, as spiral waves with left and right twists can emerge under the same conditions, resulting in flow structures varying from spatial rings to rhombic forms. The most intense motion of this type occurs near the walls. The second type of secondary flow has the form of travelling waves driven by inertial effects with characteristics very distinct from the shear waves. Its critical Reynolds number increases proportionally to 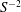$S^{-2}$, where 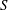$S$ denotes the groove amplitude, while the amplification rates increase proportionally to 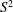$S^{2}$. These waves exist only if 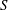$S$ is above a well-defined minimum and their axisymmetric forms dominate, with the most intense motion occurring near the annulus mid-section. Geometries that give preference to the latter waves have been identified. It is shown that the drag-reducing topographies stabilize the classical travelling waves; these waves are driven by viscous shear, so reduction of this shear decreases their amplification. The same topographies destabilize the new waves; these waves are driven by an inviscid mechanism associated with the formation of circumferential inflection points, and an increase of the groove amplitude increases their amplification. The flow conditions when the presence of grooves can be ignored, i.e. the annuli can be treated as being hydraulically smooth, have been determined.

JFM classification

Flow Control: Drag reduction Flow Control: Instability control Flow Control: Mixing enhancement
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , pp. 328 - 362
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aref, H. 1984 Stirring by chaotic advection. J. Fluid Mech. 143, 1–21.10.1017/S0022112084001233Google Scholar
Arnal, D., Perraud, J. & Seraudie, A. 2008 Attachment line and surface imperfection problems. In RTO-AVT/VKI Lecture Series ‘Advances in Laminar–Turbulent Transition Modeling’, The Von Karman Institute for Fluid Dynamics.Google Scholar
Asai, M. & Floryan, J. M. 2006 Experiments on the linear instability of flow in a wavy channel. Eur. J. Mech. (B/Fluid) 25, 971–986.10.1016/j.euromechflu.2006.03.002Google Scholar
Baines, P. G., Majumdar, S. J. & Mitsudera, H. 1996 The mechanics of the Tollmien–Schlichting wave. J. Fluid Mech. 312, 107–124.10.1017/S0022112096001930Google Scholar
Bayly, B. J., Orszag, S. A. & Herbert, T. 1988 Instability mechanisms in shear-flow transition. Annu. Rev. Fluid Mech. 20, 359–391.10.1146/annurev.fl.20.010188.002043Google Scholar
Burridge, M. & Draizin, P. G. 1969 Comments on stability of pipe Poiseuille flow. Phys. Fluids 12, 264–265.10.1063/1.1692286Google Scholar
Cabal, A., Szumbarski, J. & Floryan, J. M. 2001 Numerical simulation of flows over corrugated walls. Comput. Fluids 30, 753–776.10.1016/S0045-7930(00)00028-1Google Scholar
Canuto, C., Hussaini, M. Y., Quarternoi, A. & Zang, T. A. 2006 Spectral Methods: Fundamentals in Single Domains. Springer.Google Scholar
Carlsson, F., Sen, M. & Löfdahl, L. 2005 Fluid mixing induced by vibrating walls. Eur. J. Mech. (B/Fluids) 24, 366–378.10.1016/j.euromechflu.2004.10.006Google Scholar
Chen, Y., Floryan, J. M., Chew, Y. T. & Khoo, B. C. 2016 Groove-induced changes of discharge in channel flows. J. Fluid Mech. 799, 297–333.10.1017/jfm.2016.388Google Scholar
DeGroot, C. T., Wang, C. & Floryan, J. M. 2016 Drag reduction due to streamwise grooves in turbulent channel flow. Trans. ASME J. Fluid Engng 138 (12), 121201.Google Scholar
Demmel, J. W. 1997 Applied Numerical Linear Algebra. SIAM.10.1137/1.9781611971446Google Scholar
Dou, H. S., Khoo, B. C. & Tsai, H. M. 2010 Determining the critical conditions of turbulent transition in a fully developed annulus flow. J. Petrol. Sci. Engng 73, 41–47.10.1016/j.petrol.2010.05.003Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability, 2nd edn. Cambridge University Press.10.1017/CBO9780511616938Google Scholar
Fiebig, M. 1995a Embedded vortices in internal flow: heat transfer and pressure loss enhancement. Intl J. Heat Fluid Flow 16, 376–388.10.1016/0142-727X(95)00043-PGoogle Scholar
Fiebig, M. 1995b Vortex generators for compact heat exchangers. J. Enhanced Heat Transfer 2, 43–61.10.1615/JEnhHeatTransf.v2.i1-2.60Google Scholar
Fiebig, M. 1998 Vortices, generators and heat transfer. Chem. Engng Res. Des. 76 (2), 108–123.10.1205/026387698524686Google Scholar
Fiebig, M. & Chen, Y. 1999 Heat transfer enhancement by wing-type longitudinal vortex generators and their application to finned oval tube heat exchanger elements. In Heat Transfer Enhancement of Heat Exchangers (ed. Kakac, S., Bergles, A. E., Mayinger, F. & Yuncu, H.), NATO ASI Series, pp. 79–105. Springer.10.1007/978-94-015-9159-1_6Google Scholar
Fjørtoft, R. 1950 Application of integral theorems in deriving criteria of stability for laminar flows and for the baroclinic circular vortex. Geophys. Publ. 17, 1–52.Google Scholar
Floryan, J. M. 2003 Vortex instability in a diverging–converging channel. J. Fluid Mech. 482, 17–50.10.1017/S0022112003003987Google Scholar
Floryan, J. M. 2007 Three-dimensional instabilities of laminar flow in a rough channel and the concept of hydraulically smooth wall. Eur. J. Mech. (B/Fluid) 26, 305–329.10.1016/j.euromechflu.2006.07.002Google Scholar
Floryan, J. M. 2015 Flow in a meandering channel. J. Fluid Mech. 770, 52–84.10.1017/jfm.2015.135Google Scholar
Floryan, J. M. & Asai, M. 2011 On the transition between distributed and isolated surface roughness and its effect on the stability of channel flow. Phys. Fluids 23, 104101.10.1063/1.3644694Google Scholar
Garg, V. K. 1980 Spatial stability of concentric annular flow. J. Phys. Soc. Japan 49, 1577–1583.10.1143/JPSJ.49.1577Google Scholar
Gepner, S. W. & Floryan, J. M. 2016 Flow dynamics and enhanced mixing in a converging–diverging channel. J. Fluid Mech. 807, 167–204.10.1017/jfm.2016.621Google Scholar
Heaton, C. J. 2008 Linear instability of annular Poiseuille flow. J. Fluid Mech. 610, 391–406.10.1017/S0022112008002577Google Scholar
Henningson, D. S.1987 Stability of parallel inviscid shear flow with mean spanwise variation. Tech. Rep. TN 1987-57. NASA STI/Recon Technical Report.Google Scholar
Ho, H. Q. & Asai, M. 2018 Experimental study on the stability of laminar flow in a channel with streamwise and oblique riblets. Phys. Fluids 30, 024106.10.1063/1.5009039Google Scholar
Husain, S. Z. & Floryan, J. M. 2008 Implicit spectrally-accurate method for moving boundary problems using immersed boundary conditions concept. J. Comput. Phys. 227, 4459–4477.10.1016/j.jcp.2008.01.002Google Scholar
Husain, S. Z., Szumbarski, J. & Floryan, J. M. 2009 Over-constrained formulation of the immersed boundary condition method. Comput. Meth. Appl. Mech. 199, 94–112.10.1016/j.cma.2009.09.022Google Scholar
Ishida, T., Duguet, Y. & Tsukahara, T. 2016 Transitional structures in annular Poiseuille flow depending on radius ratio. J. Fluid Mech. 794, R2–1–R2–11.10.1017/jfm.2016.192Google Scholar
Jacobi, A. M. & Shah, R. K. 1995 Heat transfer surface enhancement through the use of longitudinal vortices: a review of recent progress. Exp. Therm. Fluid Sci. 11, 295–309.10.1016/0894-1777(95)00066-UGoogle Scholar
Jiménez-Lozano, J., Sen, M. & Dunn, P. F. 2009 Particle motion in unsteady two-dimensional peristaltic flow with application to the ureter. Phys. Rev. E 79, 041901.Google Scholar
Joseph, D. D. 1976 Stability of Fluid Motions. Springer.Google Scholar
Lin, C. C. 1945 On the stability of two-dimensional parallel flows: Part I–general theory. Q. Appl. Maths 3, 117–142.10.1090/qam/13983Google Scholar
Mack, L. M. 1976 A numerical study of the temporal eigenvalue spectrum of the blasius boundary layer. J. Fluid. Mech. 73, 497–520.10.1017/S002211207600147XGoogle Scholar
Mahadevan, R. & Lilley, G. M. 1977 The stability of axial flow between concentric cylinders to asymmetric disturbances. In AGARD Laminar–Turbulent Transition, vol. 224, pp. 1–10.Google Scholar
Mohammadi, A. & Floryan, J. M. 2012 Mechanism of drag generation by surface corrugation. Phys. Fluids 24, 013602.10.1063/1.3675557Google Scholar
Mohammadi, A. & Floryan, J. M. 2013a Groove optimization for drag reduction. Phys. Fluids 25, 113601.10.1063/1.4826983Google Scholar
Mohammadi, A. & Floryan, J. M. 2013b Pressure losses in grooved channel. J. Fluid. Mech. 725, 23–54.10.1017/jfm.2013.184Google Scholar
Mohammadi, A., Moradi, H. V. & Floryan, J. M. 2015 New instability mode in a grooved channel. J. Fluid Mech. 778, 691–720.10.1017/jfm.2015.399Google Scholar
Moradi, H. V., Budiman, A. C. & Floryan, J. M. 2017 Use of natural instabilities for generation of streamwise vortices in a laminar channel flow. Theor. Comput. Fluid Dyn. 31, 233–250.10.1007/s00162-016-0418-5Google Scholar
Moradi, H. V. & Floryan, J. M. 2012 Algorithm for analysis of flows in ribbed annuli. Intl J. Numer. Meth. Fluids 68, 805–838.10.1002/fld.2581Google Scholar
Moradi, H. V. & Floryan, J. M. 2013a Flows in annuli with longitudinal grooves. J. Fluid Mech. 716, 280–315.10.1017/jfm.2012.547Google Scholar
Moradi, H. V. & Floryan, J. M. 2013b Maximization of heat transfer across micro-channels. Intl J. Heat Mass Transfer 66, 517–530.10.1016/j.ijheatmasstransfer.2013.07.059Google Scholar
Moradi, H. V. & Floryan, J. M. 2014 Stability of flow in a channel with longitudinal grooves. J. Fluid Mech. 757, 613–648.10.1017/jfm.2014.508Google Scholar
Moradi, H. V. & Floryan, J. M. 2016a A method for analysis of stability of flows in ribbed annuli. J. Comput. Phys. 314, 35–59.10.1016/j.jcp.2016.02.069Google Scholar
Moradi, H. V. & Floryan, J. M. 2016b Sliding Couette flow in a ribbed annulus. Phys. Fluids 28, 074103.10.1063/1.4955101Google Scholar
Moradi, H. V. & Floryan, J. M. 2017a Algorithm for analysis of peristaltic annular flows. Comput. Fluids 147, 72–89.10.1016/j.compfluid.2017.01.020Google Scholar
Moradi, H. V. & Floryan, J. M. 2017b On the mixing enhancement in annular flows. Phys. Fluids 29, 024106.10.1063/1.4976325Google Scholar
Morkovin, M. V. 1990 On roughness-induced transition: facts, views and speculations. In Instability and Transition (ed. Hussaini, M. Y. & Voigt, R. G.), vol. 1, pp. 281–295. Springer.Google Scholar
Mott, J. E. & Joseph, D. D. 1968 Stability of parallel flow between concentric cylinders. Phys. Fluids 11, 2065–2073.10.1063/1.1691784Google Scholar
Orszag, S. A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 689–703.10.1017/S0022112071002842Google Scholar
Rayleigh, L. 1880 On the stability or instability of certain fluid motions. Proc. Lond. Math. Soc. 11, 57–70.Google Scholar
Saad, Y. 2003 Iterative Methods for Sparse Linear Systems. SIAM.10.1137/1.9780898718003Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.10.1146/annurev.fluid.38.050304.092139Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transient in Shear Flows. Springer.10.1007/978-1-4613-0185-1Google Scholar
Selverov, K. P. & Stone, H. A. 2001 Peristaltically driven channel flow with applications toward micromixing. Phys. Fluids 13, 1837–1859.10.1063/1.1377616Google Scholar
Shapiro, I., Shtilman, S. L. & Tumin, A. 1999 On stability of flow in an annular channel. Phys. Fluids 11, 2984–2992.10.1063/1.870179Google Scholar
Squire, H. B. 1933 On the stability of three-dimensional distribution of viscous fluid between parallel walls. Proc. R. Soc. Lond. A 142, 621–628.10.1098/rspa.1933.0193Google Scholar
Stroock, A. D., Dertinger, S. K. W., Ajdari, A., Mezic, I., Stone, H. A. & Whitesides, G. M. 2002 Chaotic mixer for microchannels. Science 295, 647–651.10.1126/science.1066238Google Scholar
Sturman, S., Ottino, J. M. & Wiggins, S. 2006 The Mathematical Foundations of Mixing. Cambridge University Press.10.1017/CBO9780511618116Google Scholar
Szumbarski, J. & Floryan, J. M. 1999 A direct spectral method for determination of flows over corrugated boundaries. J. Comput. Phys. 153, 378–402.10.1006/jcph.1999.6282Google Scholar
Szumbarski, J. & Floryan, J. M. 2006 Transient disturbance growth in a corrugated channel. J. Fluid Mech. 568, 243–272.10.1017/S0022112006002023Google Scholar
Thorpe, S. A. 1969 Experiments on the instability of stratified shear flows: immiscible fluids. J. Fluid Mech. 39, 25–48.10.1017/S0022112069002023Google Scholar
Walsh, M. J. 1983 Riblets as a viscous drag reduction technique. AIAA J. 21, 485–486.10.2514/3.60126Google Scholar
Webb, R. L. & Bergles, A. E. 1983 Performance evaluation criteria for selection of heat transfer surface geometries used in low Reynolds number heat exchangers. In Low Reynolds Number Flow Heat Exchangers, pp. 735–752. Hemisphere Publishing.Google Scholar
Yadav, N., Gepner, S. W. & Szumbarski, J. 2017 Instability in a channel with grooves parallel to the flow. Phys. Fluids 29, 084104.10.1063/1.4997950Google Scholar