No CrossRef data available.
Published online by Cambridge University Press: 15 November 2024
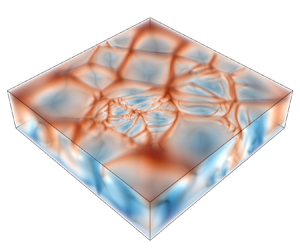
Geothermal gradients and heterogeneous permeability are commonly observed in natural geological formations for underground CO $_2$ sequestration. In this study, we conduct three-dimensional direct numerical simulations on the double-diffusive convection with both unstable temperature and concentration gradients in homogeneous and heterogeneous porous media. For homogeneous porous media, the root-mean-squared velocity increases linearly with density ratio defined as the buoyancy ratio by temperature and concentration differences. The flow structures show no remarkable changes when temperature Rayleigh number
$_2$ sequestration. In this study, we conduct three-dimensional direct numerical simulations on the double-diffusive convection with both unstable temperature and concentration gradients in homogeneous and heterogeneous porous media. For homogeneous porous media, the root-mean-squared velocity increases linearly with density ratio defined as the buoyancy ratio by temperature and concentration differences. The flow structures show no remarkable changes when temperature Rayleigh number  ${Ra}_T$ is less than its critical value, but alter from sheet-like to cellular structures as
${Ra}_T$ is less than its critical value, but alter from sheet-like to cellular structures as  ${Ra}_T$ surpasses this threshold. The concentration wavenumber scales approximately as
${Ra}_T$ surpasses this threshold. The concentration wavenumber scales approximately as  $k_{rS}\sim {Ra}_e^{0.47}$ with a defined effective Rayleigh number
$k_{rS}\sim {Ra}_e^{0.47}$ with a defined effective Rayleigh number  ${Ra}_e$. By using a scale analysis, the concentration flux exhibits a consistent linear relation with the total driving forces for all simulations. For heterogeneous porous media, where the Dykstra–Parsons coefficient
${Ra}_e$. By using a scale analysis, the concentration flux exhibits a consistent linear relation with the total driving forces for all simulations. For heterogeneous porous media, where the Dykstra–Parsons coefficient  $V_{DP}$ and correlation length
$V_{DP}$ and correlation length  $l_{r}$ determine the spatial distribution of the permeability field, the flow is strengthened in places with higher permeability. The velocity and concentration flux are less affected by
$l_{r}$ determine the spatial distribution of the permeability field, the flow is strengthened in places with higher permeability. The velocity and concentration flux are less affected by  $l_{r}$ than that by
$l_{r}$ than that by  $V_{DP}$. For small correlation length, the flow structures coarsen and their characteristic width generally increases with increasing heterogeneity. For large correlation length, small structures emerge in the regions with large permeability, which can be attributed to the intensified local Rayleigh number triggering more vigorous convection there. The variations of concentration flux with
$V_{DP}$. For small correlation length, the flow structures coarsen and their characteristic width generally increases with increasing heterogeneity. For large correlation length, small structures emerge in the regions with large permeability, which can be attributed to the intensified local Rayleigh number triggering more vigorous convection there. The variations of concentration flux with  $l_{r}$ and
$l_{r}$ and  $V_{DP}$ can be explained by the portion of area covered by high concentration with large vertical velocity near the boundaries.
$V_{DP}$ can be explained by the portion of area covered by high concentration with large vertical velocity near the boundaries.