Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T00:28:12.598Z Has data issue: false hasContentIssue false
  • English
  • Français

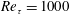DNS of a turbulent Couette flow at constant wall transpiration up to $Re_{\unicode[STIX]{x1D70F}}=1000$

Published online by Cambridge University Press:  27 November 2017

S. Kraheberger ,
S. Hoyas Open the ORCID record for S. Hoyas [Opens in a new window]  and
M. Oberlack
S. Kraheberger
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, Otto-Berndt-Str. 2, 64287 Darmstadt, Germany Graduate School of Excellence Computational Engineering, TU Darmstadt, Dolivostrasse 15, 64293 Darmstadt, Germany
S. Hoyas*
Affiliation:
Instituto de Matemática Pura y Aplicada, Universitat Politècnica de València, Camino de Vera, 46024 València, Spain
M. Oberlack
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, Otto-Berndt-Str. 2, 64287 Darmstadt, Germany Graduate School of Excellence Computational Engineering, TU Darmstadt, Dolivostrasse 15, 64293 Darmstadt, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

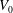We present a new set of direct numerical simulation data of a turbulent plane Couette flow with constant wall-normal transpiration velocity $V_{0}$, i.e. permeable boundary conditions, such that there is blowing on the lower side and suction on the upper side. Hence, there is no net change in flux to preserve periodic boundary conditions in the streamwise direction. Simulations were performed at 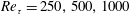$Re_{\unicode[STIX]{x1D70F}}=250,500,1000$ with varying transpiration rates in the range 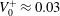$V_{0}^{+}\approx 0.03$ to 0.085. Additionally, a classical Couette flow case at 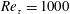$Re_{\unicode[STIX]{x1D70F}}=1000$ is presented for comparison. As a first key result we found a considerably extended logarithmic region of the mean velocity profile, with constant indicator function 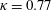$\unicode[STIX]{x1D705}=0.77$ as transpiration increases. Further, turbulent intensities are observed to decrease with increasing transpiration rate. Mean velocities and intensities collapse only in the cases where the transpiration rate is kept constant, while they are largely insensitive to friction Reynolds number variations. The long and wide characteristic stationary rolls of classical turbulent Couette flow are still present for all present DNS runs. The rolls are affected by wall transpiration, but they are not destroyed even for the largest transpiration velocity case. Spectral information indicates the prevalence of the rolls and the existence of wide structures near the blowing wall. The statistics of all simulations can be downloaded from the webpage of the Chair of Fluid Dynamics.

JFM classification

Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulence theory Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 835 , 25 January 2018 , pp. 421 - 443
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
Avsarkisov, V., Hoyas, S., Oberlack, M. & García-Galache, J. P. 2014a Turbulent plane Couette flow at moderately high Reynolds number. J. Fluid Mech. 751, R1.CrossRefGoogle Scholar
Avsarkisov, V., Oberlack, M. & Hoyas, S. 2014b New scaling laws for turbulent Poiseuille flow with wall transpiration. J. Fluid Mech. 746, 99–122.CrossRefGoogle Scholar
Bech, K., Tillmark, N., Alfredsson, P. & Andersson, H. 1995 An investigation of turbulent plane Couette flow at low Reynolds numbers. J. Fluid Mech. 286, 291–325.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 758, 327–343.Google Scholar
Bobke, A., Örlü, R. & Schlatter, P. 2015 Simulations of turbulent asymptotic suction boundary layers. J. Turbul. 17 (2), 157–180.CrossRefGoogle Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.CrossRefGoogle Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. J. Phys. A 2 (5), 765–777.Google Scholar
Del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20 (10), 101511.CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergent zones in turbulent flows. In Proceedings of the 1988 Summer Program, Center for Turbulence Research. Stanford University.Google Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. A 365, 647–664.CrossRefGoogle ScholarPubMed
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jiménez, J., Uhlman, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.CrossRefGoogle Scholar
Kametani, Y., Fukagata, K., Örlü, R. & Schlatter, P. 2015 Effect of uniform blowing suction in a turbulent boundary layer at moderate Reynolds number. Intl J. Heat Fluid Flow 55, 132–142.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channels flows at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kitoh, O., Nakabyashi, K. & Nishimura, F. 2005 Experimental study on mean velocity and turbulence characteristics of plane Couette flow: low-Reynolds-number effects and large longitudinal vortical structure. J. Fluid Mech. 539, 199–227.CrossRefGoogle Scholar
Kitoh, O. & Umeki, M. 2008 Experimental study on large-scale streak structure in the core region of turbulent plane Couette flow. Phys. Fluids 20 (2), 025107.CrossRefGoogle Scholar
Komminaho, J., Lundbladh, A. & Johansson, A. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–258.CrossRefGoogle Scholar
Lam, K. & Banerjee, S. 1992 On teh condition of streak formation in a bounded turbulent flow. Phys. Fluids 4, 306–320.CrossRefGoogle Scholar
Lee, M. & Moser, R. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lee, M. & Moser, R. 2017 Extreme-scale motions in turbulent plane Couette flows. J. Fluid Mech.; (under consideration for publication), http://arxiv.org/abs/1706.09800.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.CrossRefGoogle Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.CrossRefGoogle Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2011 Large-scale motions and inner/outer layer interactions in turbulent Couette–Poiseuille flows. J. Fluid Mech. 680, 534–563.CrossRefGoogle Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2014 Turbulence statistics in Couette flow at high Reynolds number. J. Fluid Mech. 758, 323–343.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2011 Turbulent asymptotic suction boundary layers studied by simulation. J. Phys. Conf. Ser. 318, 022020.CrossRefGoogle Scholar
Spalart, P. R. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96 (2), 297–324.CrossRefGoogle Scholar
Sumitani, Y. & Kasagi, N. 1995 Direct numerical simulation of turbulent transport with uniform wall injection and suction. AIAA J. 33, 1220–1228.CrossRefGoogle Scholar
Tillmark, N.1995 Experiments on transition and turbulence in plane Couette flow. PhD thesis, KTH, Royal Institute of Technology.Google Scholar
Tsukahara, T., Kawamura, H. & Shingai, K. 2006 DNS of turbulent Couette flow with emphasis on the large-scale structure in the core region. J. Turbul. 7, 1–16.CrossRefGoogle Scholar
Zhapbasbaev, U. K. & Isakhanova, G. Z. 1998 Developed turbulent flow in a plane channel with simultaneous injection through one porous wall and suction through the other. J. Appl. Mech. Tech. Phys. 39, 53.CrossRefGoogle Scholar