Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T01:15:57.009Z Has data issue: false hasContentIssue false
  • English
  • Français

DNS of a turbulent boundary layer with surface roughness

Published online by Cambridge University Press:  24 July 2013

James Cardillo ,
Yi Chen ,
Guillermo Araya ,
Jensen Newman ,
Kenneth Jansen  and
Luciano Castillo
James Cardillo
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180, USA
Yi Chen
Affiliation:
Department of Mechanical, Aerospace, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180, USA
Guillermo Araya*
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock TX 79401, USA
Jensen Newman
Affiliation:
Department of Mathematical Sciences, Rensselaer Polytechnic Institute, Troy, NY 12180, USA Department of Mechanical Engineering, Texas Tech University, Lubbock TX 79401, USA
Kenneth Jansen
Affiliation:
University of Colorado at Boulder, Boulder, CO 80309, USA
Luciano Castillo
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock TX 79401, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A pioneer direct numerical simulation (DNS) of a turbulent boundary layer at 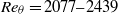$R{e}_{\theta } = 2077{{\unicode{x2013}}}2439$, was performed, on a rough surface and with a zero pressure gradient (ZPG). The boundary layer was subjected to transitional, 24-grit sandpaper surface roughness, with a roughness parameter of 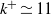${k}^{+ } \simeq 11$. The computational method involves a synergy of the dynamic multi-scale approach devised by Araya et al. (2011) for prescribing inlet turbulent boundary conditions and a new methodology for mapping high-resolution topographical surface data into a computational fluid dynamics (CFD) environment. It is shown here that the dynamic multi-scale approach can be successfully extended to simulations which incorporate surface roughness. The DNS results demonstrate good agreement with the laser Doppler anemometry (LDA) measurements performed by Brzek et al. (2008) and Schultz & Flack (2003) under similar conditions in terms of mean velocity profiles, Reynolds stresses and flow parameters, such as the skin friction coefficient, boundary and momentum thicknesses. Further, it is demonstrated that the effects of the surface roughness on the Reynolds stresses, at the values of 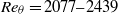$R{e}_{\theta } = 2077{{\unicode{x2013}}}2439$, are scale-dependent. Roughness effects were mainly manifested up to 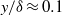$y/ \delta \approx 0. 1$. Generally speaking, it was observed that inner peak values of Reynolds stresses increased when considering outer units. However, decreases were seen in inner units. In the outer region, the most significant differences between the present DNS smooth and rough cases were computed in the wall-normal component 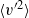$\langle {v}^{\prime 2} \rangle $ of the Reynolds stresses and in the Reynolds shear stresses 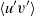$\langle {u}^{\prime } {v}^{\prime } \rangle $ in outer units. From the resulting flow fields a proper orthogonal decomposition (POD) analysis is performed and the effects of the surface roughness are distinctly observed in the most energetic POD modes. The POD analysis shows that the surface roughness causes a redistribution of the kinetic energy amongst the POD modes with energy being shifted from low-order to high-order modes in the rough case versus the smooth case. Also, the roughness causes a marked decrease in the characteristic wavelengths observed in the POD modes, particularly in the streamwise component of the velocity field. Low-order modes of the streamwise component demonstrated characteristic wavelengths of the order of 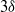$3\delta $ in the smooth case, whereas the same modes for the rough case demonstrated characteristic wavelengths of only 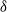$\delta $.

JFM classification

Boundary Layers: Boundary Layers Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 729 , 25 August 2013 , pp. 603 - 637
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R., Meinhart, C. & Tomkins, C. 2000 Vortex organization in the outer region. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Araya, G. & Castillo, L. 2012 DNS of turbulent thermal boundary layers up to $R{e}_{\theta } = 2300$ . Intl J. Heat Mass Transfer 55, 4003–4019.Google Scholar
Araya, G., Castillo, L. & Jansen, K. 2013 DNS of stable spatially-developing turbulent thermal boundary layers under weak stratification. In Springer Proceedings in Physics, vol. 149, Progress in Turbulence V (ed. Talamelli, A., Oberlack, M. & Peinke, J.). Proceedings of the iTi Conference in Turbulence 2012, Springer.Google Scholar
Araya, G., Castillo, L., Meneveau, C. & Jansen, K. 2011 A dynamic multi-scale approach for turbulent inflow boundary conditions in spatially evolving flows. J. Fluid Mech. 670, 581–605.Google Scholar
Araya, G., Jansen, K. & Castillo, L. 2009 Inlet condition generation for spatially developing turbulent boundary layers via multi-scale similarity. J. Turbul. 10 (36), 1–33.Google Scholar
Aubry, N., Guyonnet, R. & Lima, R. 1992 Spatio-temporal symmetries and bifurcations via bi-orthogonal decompositions. J. Nonlinear Sci. 2, 183–215.Google Scholar
Baltzer, J., Adrian, R. & Wu, X. 2010 Turbulent boundary layer structure identification via POD. Stanford Center for Turbulence Research Summer Program 2010, pp. 55–64.Google Scholar
Brzek, B., Bailon-Cuba, J., Leonardi, S. & Castillo, L. 2009 Theoretical evaluation of the Reynolds shear stress and flow parameters in transitionally rough turbulent boundary layers. J. Turbul. 10, 1–28.Google Scholar
Brzek, B., Cal, R. B., Johansson, G. & Castillo, L. 2008 Transitionally rough zero pressure gradient turbulent boundary layers. Exp. Fluids 44, 115–124.CrossRefGoogle Scholar
Cal, R., Brzek, B., Johansson, T. & Castillo, L. 2009 The rough favourable pressure gradient turbulent boundary layer. J. Fluid Mech. 641, 129–155.Google Scholar
Castillo, L. & Johansson, G. 2002 The effects of upstream conditions on a low Reynolds number turbulent boundary layer with zero pressure gradient. J. Turbul. 3, 1–19.CrossRefGoogle Scholar
Choi, H. & Moin, P. 1995 Effects of the computational time step on numerical solutions of turbulent flow. J. Comput. Phys. 113, 1–4.Google Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aeronaut. Sci. 21, 91–108.CrossRefGoogle Scholar
George, W. & Castillo, L. 1997 Zero-pressure-gradient turbulent boundary layer. Appl. Mech. Rev. 50, 689–729.Google Scholar
George, J., Simone, A. D., Iaccarino, G. & Jiménez, J. 2010 Modelling roughness effects in turbulent boundary layers by elliptic relaxation. Cent. Turbul. Res. 36, 119–128.Google Scholar
Hama, F. R. 1945 Boundary-layer characteristics for smooth and rough surfaces. Soc. Nav. Archit. Nav. Eng. 62, 333–358.Google Scholar
Holmes, P., Lumley, J. & Berkooz, G. 1997 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.Google Scholar
Hong, J., Katz, J. & Schultz, M. 2011 Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Khujadze, G. & Oberlack, M. 2004 DNS and scaling laws from new symmetry groups of ZPG turbulent boundary layer flow. Theor. Comput. Fluid Dyn. 18, 391–411.Google Scholar
Kim, J. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 129, 133–166.CrossRefGoogle Scholar
Krogstad, P., Antonia, R. & Browne, L. W. B. 1992 Comparison between rough- and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.CrossRefGoogle Scholar
Krogstad, P.-A. & Efros, V. 2012 About turbulence statistics in the outer part of a boundary layer developing over two-dimensional surface roughness. Phys. Fluids 24 (7), 075112.Google Scholar
Kunkel, G. & Marusic, I. 2006 Study of the near-wall turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Leonardi, S., Orlandi, P., Smalley, R., Djenidi, L. & Antonia, R. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.Google Scholar
Liu, Z.-C., Adrian, R. & Hanratty, T. 2001 Large-scale models of turbulent channel flow: transport and structure. J. Fluid Mech. 448, 53–80.Google Scholar
Lund, T., Wu, X. & Squires, K. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140, 233–258.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539–578.CrossRefGoogle Scholar
Moin, P. & Moser, R. 1989 Characteristic-eddy decomposition of turbulence in a channel. J. Fluid Mech. 200, 471–509.Google Scholar
Nikuradse, J. 1933 Laws of flow in rough pipes. NACA TM 1292.Google Scholar
Perry, A. & Jourbert, P. 1963 Rough wall boundary layers in adverse pressure gradients. J. Fluid Mech. 17, 193–211.CrossRefGoogle Scholar
Perry, A., Lim, K. & Henbest, S. 1987 An experimental study of the turbulent structure in smooth- and rough-wall boundary layers. J. Fluid Mech. 177, 437–466.Google Scholar
Raupach, M. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.CrossRefGoogle Scholar
Rotta, J. C. 1960 Turbulent boundary layers with heat transfer in compressible flow. AGARD Report 281.Google Scholar
Schlichting, H. 1979 Boundary-Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Schultz, M. & Flack, K. 2003 Turbulent boundary layers over surfaces smoothed by sanding. Trans. ASME: J. Fluids Engng 125, 863–870.Google Scholar
Schultz, M. & Flack, K. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.CrossRefGoogle Scholar
Scotti, A. 2007 Direct numerical simulation of turbulent channel flows with boundary roughened with virtual sandpaper. Phys. Fluids 18, 031701.Google Scholar
Simens, M., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228, 4218–4231.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Parts 1, 2 and 3. Q. Appl. Maths XLV, 561–590.CrossRefGoogle Scholar
Stolz, S. & Adams, N. A. 2003 Large-eddy simulation of high-Reynolds-number supersonic boundary layers using the approximate deconvolution model and a rescaling and recycling technique. Phys. Fluids 15, 2398–2412.Google Scholar
Sun, C. 2008 Parallel algebraic multigrid for the pressure Poisson equation in a finite element Navier–Stokes solver. PhD dissertation, Rensselaer Polytechnic Institute.Google Scholar
Townsend, A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
White, F. M. 1974 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Whiting, C. & Jansen, K. 2001 A stabilized finite element method for incompressible Navier–Stokes equations using a hierarchical basis. Intl J. Numer. Meth. Fluids 35, 93–116.Google Scholar
Wu, X. & Moin, P. 2010 Transitional and turbulent boundary layer with heat transfer. Phys. Fluids 22, 085105.Google Scholar