Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T04:29:26.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Distributed vortex-wave interactions: the relation of self-similarity to the attached eddy hypothesis

Published online by Cambridge University Press:  04 August 2021

Hugh M. Blackburn Open the ORCID record for Hugh M. Blackburn [Opens in a new window] ,
Kengo Deguchi Open the ORCID record for Kengo Deguchi [Opens in a new window]  and
Philip Hall Open the ORCID record for Philip Hall [Opens in a new window]
Hugh M. Blackburn*
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC 3800, Australia
Kengo Deguchi*
Affiliation:
School of Mathematics, Monash University, Clayton, VIC 3800, Australia
Philip Hall*
Affiliation:
School of Mathematics, Monash University, Clayton, VIC 3800, Australia
*
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

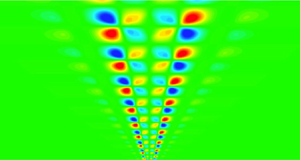
A large-Reynolds-number asymptotic reduction of the Navier–Stokes equations capable of describing a locally periodic vortex-wave array and the associated large-scale variation of the mean-shear velocity field first suggested in Hall (J. Fluid Mech., vol. 850, 2018, pp. 46–82) is extended. The sustaining process of the locally periodic coherent structures is based on the vortex-wave interaction theory of Hall & Smith (J. Fluid Mech., vol. 227, 1991, 641–666), wherein two-dimensional roll–streak fields are supported by localised nonlinear self-interactions of three-dimensional waves that are largest in size within critical layers of the streak field. The variation of the mean velocity is made possible by incorporating a slow change to the mean profile using a Wentzel–Kramers–Brillouin-type approach. As the first extension, we demonstrate that the local structure corresponds to the asymptotic limit of computations in a shearing box. A variety of solutions with different symmetry properties are found via the hybrid numerical asymptotic approach of Blackburn, Hall & Sherwin (J. Fluid Mech. vol. 721, 2013, 58–85). Moreover, some solutions show generic flow features such as uniform momentum zones and spatial intermittency known to occur in near-wall turbulent boundary layers. We extend the vortex-wave interaction array theory to show that, in addition to a Reynolds-averaged-Navier–Stokes-type relationship between the large-scale vertical variation of the mean flow and local roll–streak scale, a higher-order analysis gives a second constraint on the slow-scale dynamics. Those constraints are used for the first time to derive the logarithmic law of the wall through a closed asymptotic analysis of self-similar local coherent structures, consistent with the attached eddy hypothesis.

JFM classification

Aerodynamics: High-speed flow Waves/Free-surface Flows: Critical layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 924 , 10 October 2021 , A8
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adrian, R.J., Meinhart, C.D. & Tomkins, C.D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Bakken, O.M., Krogstad, P.-A., Ashrafian, A. & Andersson, H.I. 2005 Reynolds number effects in the outer layer of the turbulent flow in a channel with rough walls. Phys. Fluids 17 (6), 065101.CrossRefGoogle Scholar
Batchelor, G.K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1 (2), 177–190.CrossRefGoogle Scholar
Batchelor, G.K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Beaume, C., Chini, G.P., Julien, K. & Knobloch, E. 2015 Reduced description of exact coherent states in parallel shear flows. Phys. Rev. E 91, 043010.CrossRefGoogle ScholarPubMed
Beaume, C., Knobloch, E., Chini, G.P. & Julien, K. 2016 Modulated patterns in a reduced model of a transitional shear flow. Phys. Scr. 91, 024003.CrossRefGoogle Scholar
Benney, D.J. & Chow, K. 1989 A mean flow first harmonic theory for hydrodynamic instabilities. Stud. Appl. Maths 80 (1), 37–83.CrossRefGoogle Scholar
Blackburn, H.M., Hall, P. & Sherwin, S.J. 2013 Lower branch equlibria in Couette flow: the emergence of canonical states for arbitrary shear flows. J. Fluid Mech. 721, 58–85.Google Scholar
Brandenburg, A., Norlund, A., Stein, R.F. & Torkelsson, U. 1995 Dynamo-generated turbulence and large-scale magnetic fields in a Keplerian shear flow. Astrophys. J. 446, 741–754.CrossRefGoogle Scholar
Chernyshenko, S.I. & Baig, M.F. 2005 The mechanism of streak formation in near-wall turbulence. J. Fluid Mech. 544, 99–131.CrossRefGoogle Scholar
Chini, G.P., Montemuro, B., White, C.M. & Klewicki, J. 2017 A self-sustaining process model of inertial layer dynamics in high Reynolds number turbulent wall flows. Phil. Trans. R. Soc. A 375, 20160090.CrossRefGoogle ScholarPubMed
Chung, D., Monty, J. & Ooi, A. 2014 An idealised assessment of Townsend's outer-layer similarity hypothesis for wall turbulence. J. Fluid Mech. 742, R3.CrossRefGoogle Scholar
Clever, R.M. & Busse, F.H. 1992 Three-dimensional convection in a horizontal fluid layer subjected to a constant shear. J. Fluid Mech. 234, 511–527.CrossRefGoogle Scholar
Cossu, C. & Hwang, Y. 2017 Self-sustaining processes at all scales in wall-bounded turbulent shear flows. Phil. Trans. R. Soc. A 375, 20160088.CrossRefGoogle ScholarPubMed
Deguchi, K. 2015 Self-sustained states at Kolmogorov microscale. J. Fluid Mech. 781, R6.CrossRefGoogle Scholar
Deguchi, K. 2019 Inviscid instability of a unidirectional flow sheared in two transverse directions. J. Fluid Mech. 874, 979–994.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2014 a Canonical exact coherent structures embedded in high Reynolds number flows. Phil. Trans. R. Soc. A 372 (2020), 20130352.CrossRefGoogle ScholarPubMed
Deguchi, K. & Hall, P. 2014 b Free-stream coherent structures in parallel boundary-layer flows. J. Fluid Mech. 752, 602–625.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2014 c The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow. J. Fluid Mech. 750, 99–112.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2016 On the instability of vortex–wave interaction states. J. Fluid Mech. 802, 634–666.CrossRefGoogle Scholar
Deguchi, K., Hall, P. & Walton, A. 2013 The emergence of localized vortex–wave interaction states in plane Couette flow. J. Fluid Mech. 721, 58–85.CrossRefGoogle Scholar
Eckhardt, B. & Zammert, S. 2018 Small scale exact coherent structures at large Reynolds numbers in plane Couette flow. Nonlinearity 31 (2), R66–R77.CrossRefGoogle Scholar
Faisst, H. & Eckhardt, B 2003 Traveling waves in pipe flow. Phys. Rev. Let. 91 (22), 224502.CrossRefGoogle ScholarPubMed
Flores, O. & Jiménez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.CrossRefGoogle Scholar
Gerz, T., Schumann, U. & Elgobashi, S.E. 1989 Direct numerical simulation of stratified homogeneous shear flows. J. Fluid Mech. 200, 563–594.CrossRefGoogle Scholar
Gibson, J.F. & Brand, E. 2014 Spatially localized solutions of planar shear flow. J. Fluid Mech. 745, 25–61.CrossRefGoogle Scholar
Gibson, J.F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 1–24.CrossRefGoogle Scholar
Gibson, J.F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.CrossRefGoogle Scholar
Gómez, F., Pérez, J.M., Blackburn, H.M. & Theofilis, V. 2015 On the use of matrix-free shift-invert strategies for global flow instability analysis. Aerosp. Sci. Technol. 44, 69–76.CrossRefGoogle Scholar
Hall, P. 2018 Vortex–wave interaction arrays: a sustaining mechanism for the log layer? J. Fluid Mech. 850, 46–82.CrossRefGoogle Scholar
Hall, P. & Lakin, W 1988 The fully nonlinear development of Görtler vortices in growing boundary layers. Proc. R. Soc. Lond. A 415, 421–44.Google Scholar
Hall, P. & Sherwin, S.J. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.CrossRefGoogle Scholar
Hall, P. & Smith, F.T. 1988 The nonlinear interaction of Tollmein–Schlichting waves and Taylor–Görtler vortices in curved channel flows. Proc. R. Soc. Lond. A 417, 255–282.Google Scholar
Hall, P. & Smith, F.T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.CrossRefGoogle Scholar
Hamilton, J.M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Hawley, J.F., Gammie, C.F. & Balbus, S.A. 1995 Local three-dimensional magnetohydrodynamic simulations of acretion disks. Astrophys. J. 440, 792.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–29.CrossRefGoogle Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23 (6), 061702.CrossRefGoogle Scholar
Itano, T. & Generalis, S.C. 2009 Hairpin vortex solution in planar Couette flow: a tapestry of knotted vortices. Phys. Rev. Let. 102, 114501.CrossRefGoogle ScholarPubMed
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70 (3), 703–716.CrossRefGoogle Scholar
Jiménez, J. 2013 How linear is wall turbulence? Phys. Fluids 25, 110814.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Kaltenbach, H.-J., Gerz, T. & Schumann, U. 1994 Large-eddy simulation of homogeneous turbulence and diffusion in a stably stratified shear flow. J. Fluid Mech. 280, 1–40.CrossRefGoogle Scholar
von Kármán, T.. 1930 Mechanische Ähnichkeit und Turbulenz. Nach. Akad. Wiss. Gött.: Math.-Phys. Klasse 58, 58–76.Google Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44, 203–225.CrossRefGoogle Scholar
Kida, S. & Tanaka, M. 1994 Dynamics of vortical structures in a homogeneous shear flow. J. Fluid Mech. 274, 43–68.CrossRefGoogle Scholar
Kim, H.T., Kline, S.J. & Reynolds, W.C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50 (1), 133–160.CrossRefGoogle Scholar
Klewicki, J. 2013 A description of turbulent wall-flow vorticity consistent with mean dynamics. J. Fluid Mech. 737, 176–204.CrossRefGoogle Scholar
Klewicki, J. & Oberlack, M. 2015 Finite Reynolds number properties of a turbulent channel flow similarity solution. Phys. Fluids 27, 095110.CrossRefGoogle Scholar
Klewicki, J., Philip, J., Marusic, I., Chauhan, K. & Morrill-Winter, C. 2014 Self-similarity in the inertial region of wall turbulence. Phys. Rev. E 90, 063015.CrossRefGoogle ScholarPubMed
Laskari, A., de Kat, R., Hearst, R.J. & Ganapathisubramani, B. 2018 The evolution of uniform momentum zones in a turbulent boundary layer. J. Fluid Mech. 842, 554–590.CrossRefGoogle Scholar
Lozano-Durán, A. & Bae, H.J. 2019 Characteristic scales of Townsend's wall-attached eddies. J. Fluid Mech. 868, 698–725.CrossRefGoogle ScholarPubMed
Malkus, W.V.R. 1956 Outline of a theory of turbulent shear flow. J. Fluid Mech. 1 (5), 521–39.CrossRefGoogle Scholar
Marusic, I. & Monty, J.P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51, 49–74.CrossRefGoogle Scholar
McKeon, B.J. & Sharma, A.S. 2010 A critical layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Meinhart, C.D. & Adrian, R.J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7 (7), 694–696.CrossRefGoogle Scholar
Millikan, C.B. 1938 A critical discussion of turbulent flows in channels and tubes. In Proceedings of the 5th International Congress for Applied Mechanics (ed. J. P. Den Hartog & H. Peters), pp. 386–392, Wiley.Google Scholar
Mizuno, Y. & Jiménez, J. 2013 Wall turbulence without walls. J. Fluid Mech. 723, 429–455.CrossRefGoogle Scholar
Moarref, R., Sharma, A.S., Tropp, J.A. & McKeon, B.J. 2013 Model-based scaling of the streamwise energy density in high-Reynolds-number turbulent channels. J. Fluid Mech. 734, 275–316.CrossRefGoogle Scholar
Montemuro, B., White, C.M., Klewicki, J. & Chini, G.P. 2020 A self-sustaining process theory for uniform momentum zones and internal shear layers in high Reynolds number shear flows. J. Fluid Mech. 901, A28.CrossRefGoogle Scholar
Morrill-Winter, C., Philip, J. & Klewicki, J. 2017 An invariant representation of mean inertia: theoretical basis for the log layer in turbulent boundary layers. J. Fluid Mech. 813, 594–617.CrossRefGoogle Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
Perry, A.E. & Chong, M.S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A.E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Pumir, A. 1996 Turbulence in homogeneous shear flows. Phys. Fluids 8 (11), 3112–3127.CrossRefGoogle Scholar
Riols, A., Rincon, F., Cossu, C., Lesur, G., Longaretti, P.-Y., Ogilvie, G.I. & Herault, J. 2013 Global bifurcations to subcritical magnetorotational dynamo action in Keplerian shear flow. J. Fluid Mech. 731, 1–45.CrossRefGoogle Scholar
Robinson, J.L. 1967 Finite amplitude convection cells. J. Fluid Mech. 30 (3), 577–600.CrossRefGoogle Scholar
Rogallo, R.S. 1981 Numerical experiments in homogeneous turbulence. NASA Tech. Memorandum 81315.Google Scholar
Rogers, M.M. & Moin, P. 1987 The structure of the vorticity field in homogeneous turbulent flows. J. Fluid Mech. 176, 33–66.CrossRefGoogle Scholar
Schneider, T., Gibson, J.F. & Burke, J. 2010 a Snakes and ladders: localized solutions of plane Couette flow. Phys. Rev. Let. 104 (10), 104501.CrossRefGoogle ScholarPubMed
Schneider, T.M., Marinc, D. & Eckhardt, B. 2010 b Localised edge states nucleate turbulence in extended plane Couette cells. J. Fluid Mech. 646, 441–451.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Schumann, U. 1985 Algorithms for direct numerical simulation of shear-periodic turbulence. In Ninth International Conference on Numerical Methods in Fluid Dynamics (ed. Soubbaramayer & J. P. Boujot), Lecture Notes in Physics, vol. 218, pp. 492–496. Springer.CrossRefGoogle Scholar
Sekimoto, A., Dong, S. & Jiménez, J. 2016 Direct numerical simulation of statistically stationary and homogeneous shear turbulence and its relation to other shear flows. Phys. Fluids 26 (3), 035101.CrossRefGoogle Scholar
Sekimoto, A. & Jiménez, J. 2017 Vertically localised equlibrium solutions in large-eddy simulations of homogeneous shear flow. J. Fluid Mech. 827, 225–249.CrossRefGoogle Scholar
de Silva, C.M., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–321.CrossRefGoogle Scholar
de Silva, C.M., Philip, J., Hutchins, N. & Marusic, I. 2017 Interfaces of uniform momentum in turbulent boundary layers. J. Fluid Mech. 820, 451–478.CrossRefGoogle Scholar
Thomas, V.L., Lieu, B.K., Jovanović, M.R., Farrell, B.F., Ioannou, P.J. & Gayme, D.F. 2014 Self-sustaining turbulence in a restricted nonlinear model of plane Couette flow. Phys. Fluids 26, 105112.CrossRefGoogle Scholar
Townsend, A.A. 1951 The structure of the turbulent boundary layer. Math. Proc. Camb. Phil. Soc. 47, 375–395.CrossRefGoogle Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–890.CrossRefGoogle Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Let. 81 (19), 4140–4143.CrossRefGoogle Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15 (6), 1517–1534.CrossRefGoogle Scholar
Wang, J., Gibson, J.F. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Let. 98 (20), 204501.CrossRefGoogle ScholarPubMed
Wedin, H. & Kerswell, R.R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.CrossRefGoogle Scholar
Wei, W., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar
Willis, A.P., Cvitanović, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.CrossRefGoogle Scholar
Yang, Q., Willis, A.P. & Hwang, Y. 2018 Energy production and self-sustained turbulence at the Kolmogorov scale in Couette flow. J. Fluid Mech. 834, 531–554.CrossRefGoogle Scholar
Yang, Q., Willis, A.P. & Hwang, Y. 2019 Exact coherent states of attached eddies in channel flow. J. Fluid Mech. 862, 1029–1059.CrossRefGoogle Scholar