Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T22:47:43.843Z Has data issue: false hasContentIssue false
  • English
  • Français

The dissipation tensor $\unicode[STIX]{x1D700}_{ij}$ in wall turbulence

Published online by Cambridge University Press:  19 October 2016

G. A. Gerolymos  and
I. Vallet
G. A. Gerolymos
Affiliation:
Sorbonne Universités, Université Pierre-et-Marie-Curie (UPMC), 4 place Jussieu, 75005 Paris, France
I. Vallet*
Affiliation:
Sorbonne Universités, Université Pierre-et-Marie-Curie (UPMC), 4 place Jussieu, 75005 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

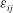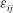The paper investigates the dissipation tensor $\unicode[STIX]{x1D700}_{ij}$ in wall turbulence. Available direct numerical simulation (DNS) data are examined to illustrate the differences in the anisotropy of the dissipation tensor $\unicode[STIX]{x1D700}_{ij}$ with respect to the anisotropy of the Reynolds stresses 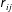$\unicode[STIX]{x1D633}_{ij}$. The budgets of the transport equations of the dissipation tensor 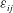$\unicode[STIX]{x1D700}_{ij}$ are studied using novel DNS data of low Reynolds number turbulent plane channel flow with spatial resolution sufficiently fine to accurately determine the correlations of products of two-derivatives of fluctuating velocities 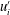$u_{i}^{\prime }$ and pressure 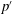$p^{\prime }$ which appear in various terms. Finally, the influence of the Reynolds number on the diagonal components of 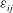$\unicode[STIX]{x1D700}_{ij}$ (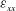$\unicode[STIX]{x1D700}_{xx}$, 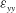$\unicode[STIX]{x1D700}_{yy}$, 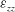$\unicode[STIX]{x1D700}_{zz}$) and on the various terms in their transport equations is studied using available DNS data of Vreman and Kuerten (Phys. Fluids, vol. 26, 2014b, 085103).

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 807 , 25 November 2016 , pp. 386 - 418
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41–L44.Google Scholar
Aris, R. 1962 Vectors, Tensors, and the Basic Equations of Fluid Mechanics, 1989 edn. Dover.Google Scholar
Ben Nasr, N., Gerolymos, G. A. & Vallet, I. 2014 Low-diffusion approximate Riemann solvers for Reynolds-stress transport. J. Comput. Phys. 268, 186–235.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.CrossRefGoogle Scholar
Bhattacharya, A., Kassinos, S. C. & Moser, R. D. 2008 Representing anisotropy of two-point second-order turbulence velocity correlations using structure tensors. Phys. Fluids 20, 101502.CrossRefGoogle Scholar
Bradshaw, P. 1967 The turbulence structure in equilibrium boundary-layers. J. Fluid Mech. 29, 625–645.Google Scholar
Buschmann, M. H. & Gad-el-Hak, M. 2007 Recent developments in scaling of wall-bounded flows. Prog. Aerosp. Sci. 42, 419–467.Google Scholar
Chang, P. A. III, Piomelli, U. & Blake, W. K. 1999 Relations between wall-pressure and velocity-field sources. Phys. Fluids 11 (11), 3434–3448.Google Scholar
Chapman, D. R. & Kuhn, G. D. 1986 The limiting behaviour of turbulence near a wall. J. Fluid Mech. 170, 265–292.Google Scholar
Chou, P. Y. 1945 On velocity correlations and the solutions of the equations of turbulent fluctuations. Q. Appl. Maths 3, 38–54.Google Scholar
Coles, D. 1956 The law of the wake in a turbulent boundary layer. J. Fluid Mech. 1, 191–226.Google Scholar
Craft, T. J. & Launder, B. 2001 Principles and performance of TCL-based second-moment closures. Flow Turbul. Combust. 66, 355–372.Google Scholar
Davidson, P. A. 2004 Turbulence. Oxford University Press.Google Scholar
Durbin, P. A. & Speziale, C. G. 1991 Local anisotropy in strained turbulence at high Reynolds numbers. Trans. ASME J. Fluids Engng 113, 707–709.CrossRefGoogle Scholar
Gerolymos, G. A., Lo, C. & Vallet, I. 2012a Tensorial representations of Reynolds-stress pressure-strain redistribution. Trans. ASME J. Appl. Mech. 79 (4), 044506.Google Scholar
Gerolymos, G. A., Lo, C., Vallet, I. & Younis, B. A. 2012b Term-by-term analysis of near-wall second moment closures. AIAA J. 50 (12), 2848–2864.CrossRefGoogle Scholar
Gerolymos, G. A., Sénéchal, D. & Vallet, I. 2009 Very-high-order WENO schemes. J. Comput. Phys. 228, 8481–8524.Google Scholar
Gerolymos, G. A., Sénéchal, D. & Vallet, I. 2010 Performance of very-high-order upwind schemes for DNS of compressible wall-turbulence. Intl J. Numer. Meth. Fluids 63, 769–810.CrossRefGoogle Scholar
Gerolymos, G. A., Sénéchal, D. & Vallet, I. 2013 Wall effects on pressure fluctuations in turbulent channel flow. J. Fluid Mech. 720, 15–65.CrossRefGoogle Scholar
Gerolymos, G. A. & Vallet, I. 2014 Pressure, density, temperature and entropy fluctuations in compressible turbulent plane channel flow. J. Fluid Mech. 757, 701–746.Google Scholar
Hanjalić, K. 1994 Advanced turbulence closure models: a view of current status and future prospects. Intl J. Heat Fluid Flow 15, 178–203.Google Scholar
Hanjalić, K. & Jakirlić, S. 1993 A model of stress dissipation in second-moment closures. Appl. Sci. Res. 51, 513–518.Google Scholar
Hinze, J. O. 1975 Turbulence, 2nd edn. McGraw-Hill.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18, 011702.Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20, 101511.CrossRefGoogle Scholar
Hu, Z. W., Morfey, C. L. & Sandham, N. D. 2002 Aeroacoustics of wall-bounded turbulent flow. AIAA J. 40 (3), 465–473.Google Scholar
Hu, Z. W., Morfey, C. L. & Sandham, N. D. 2003 Sound radiation in turbulent channel flows. J. Fluid Mech. 475, 269–302.Google Scholar
Hu, Z. W., Morfey, C. L. & Sandham, N. D. 2006 Wall pressure and shear stress spectra from direct simulations of channel flow. AIAA J. 44 (7), 1541–1549.Google Scholar
Jakirlić, S., Eisfeld, B., Jester-Zürker, R. & Kroll, N. 2007 Near-wall Reynolds-stress model calculations of transonic flow configurations relevant to aircraft aerodynamics. Intl J. Heat Fluid Flow 28, 602–615.Google Scholar
Jakirlić, S. & Hanjalić, K. 2002 A new approach to modelling near-wall turbulence energy and stress dissipation. J. Fluid Mech. 459, 139–166.Google Scholar
Jakirlić, S. & Maduta, R. 2015 Extending the bounds of steady rans closures: Toward an instability-sensitive Reynolds-stress model. Intl J. Heat Fluid Flow 51, 175–194.Google Scholar
Jovanović, J. 2004 The Statistical Dynamics of Turbulence. Springer.Google Scholar
Jovanović, J., Ye, Q. Y. & Durst, F. 1995 Statistical interpretation of the turbulent dissipation-rate in wall-bounded flows. J. Fluid Mech. 293, 321–347.Google Scholar
Kassinos, S. C., Reynolds, W. C. & Rogers, M. M. 2001 1-point turbulence structure tensors. J. Fluid Mech. 428, 213–248.Google Scholar
Khoury, G. K. E., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 DNS of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91, 475–495.Google Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel-flow. J. Fluid Mech. 205, 421–451.CrossRefGoogle Scholar
Kim, J. 2012 Progress in pipe and channel flow turbulence, 1961–2011. J. Turbul. 13, 000045.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low-Reynolds-number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kolovandin, B. A. & Vatutin, I. A. 1972 Statistical transfer theory in nonhomogeneous turbulence. Intl J. Heat Mass Transfer 15, 2371–2383.Google Scholar
Lai, Y. G. & So, R. M. C. 1990 On near-wall turbulent flow modelling. J. Fluid Mech. 221, 641–673.Google Scholar
Launder, B. E. & Reynolds, W. C. 1983 Asymptotic near-wall stress dissipation rates in a turbulent flow. Phys. Fluids 26 (5), 1157–1158.CrossRefGoogle Scholar
Launder, B. E. & Shima, N. 1989 2-moment closure for the near-wall sublayer: development and application. AIAA J. 27 (10), 1319–1325.Google Scholar
Lee, M. & Moser, R. D. 2015 DNS of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Lee, M. J. & Reynolds, W. C. 1987 On the structure of homogeneous turbulence. In Turbulent Shear Flows 5, Selected Papers for the 5th International Symposium on Turbulent Shear Flows, Cornell University, Ithaca (NY, USA), Aug 7–9, 1985 (ed. Durst, F., Launder, B. E., Lumley, J. L., Schmidt, F. W. & Whitelaw, J. H.), pp. 54–66. Springer.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26 (1), 011702.Google Scholar
Lumley, J. L. 1978 Computational modeling of turbulent flows. Adv. Appl. Mech. 18, 123–176.CrossRefGoogle Scholar
Lumley, J. L. & Newman, G. R. 1977 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 82, 161–178.Google Scholar
Lumley, J. L., Yang, Z. & Shih, T. H. 1999 A length-scale equation. Flow Turbul. Combust. 63, 1–21.Google Scholar
Mansour, N. N., Kim, J. & Moin, P. 1988 Reynolds-stress and dissipation-rate budgets in a turbulent channel flow. J. Fluid Mech. 194, 15–44.Google Scholar
Marusic, I., Mckeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathieu, J. & Scott, J. 2000 An Introduction to Turbulent Flow. Cambridge University Press.Google Scholar
Monin, A. S. & Yaglom, A. M. 1971 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 1. MIT Press.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.Google Scholar
Oberlack, M. 1997 Non-isotropic dissipation in non-homogeneous turbulence. J. Fluid Mech. 350, 351–374.CrossRefGoogle Scholar
Patel, V. C., Rodi, W. & Scheuerer, G. 1985 Turbulence models for near-wall and low-Reynolds-number flows: A review. AIAA J. 23, 1308–1319.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Riley, K. F., Hobson, M. P. & Bence, S. J. 2006 Mathematical Methods for Physics and Engineering, 3rd edn. Cambridge University Press.Google Scholar
Rivlin, R. S. 1955 Further remarks on the stress-deformation relations for isotropic materials. Indiana Univ. Math. J. 4, 681–702.Google Scholar
Rodi, W. & Mansour, N. N. 1993 Low Reynolds number k-𝜀 modelling with the aid of DNS. J. Fluid Mech. 250, 509–529.CrossRefGoogle Scholar
Schultz, M. P. & Flack, K. A. 2013 Reynolds-number scaling of turbulent channel flow. Phys. Fluids 25, 025104.Google Scholar
Schumann, U. 1977 Realizability of Reynolds-stress turbulence models. Phys. Fluids 20, 721–725.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25, 105102.Google Scholar
Simonsen, A. J. & Krogstad, P. Å. 2005 Turbulent stress invariant analysis: classification of existing terminology. Phys. Fluids 17, 088103.CrossRefGoogle Scholar
Speziale, C. G. 1989 Turbulence modeling in noninertial frames of reference. Theor. Comput. Fluid Dyn. 1, 3–19.Google Scholar
Speziale, C. G. & Gatski, T. B. 1997 Analysis and modelling of anisotropies in the dissipation rate of turbulence. J. Fluid Mech. 344, 155–180.Google Scholar
Stewart, G. W. 1998 Matrix Algorithms I. SIAM.Google Scholar
Tagawa, M., Nagano, Y. & Tsuji, T.1991 Turbulence model for the dissipation components of Reynolds stresses. In 8th Symposium on Turbulence Shear Flows, Technical University of Munich, paper 29-3.Google Scholar
Taylor, G. I. 1938 Production and dissipation of vorticity in a turbulent fluid. Proc. R. Soc. Lond. A 164, 15–23.Google Scholar
Taylor, J. R. 1997 An Introduction to Error Analysis. University Science Books.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vreman, A. W. & Kuerten, J. G. M. 2014a Comparison of DNS databases of turbulent channel flow at Re 𝜏 = 180. Phys. Fluids 26, 015102.Google Scholar
Vreman, A. W. & Kuerten, J. G. M. 2014b Statistics of spatial derivatives of velocity and pressure in turbulent channel flow. Phys. Fluids 26, 085103.Google Scholar
Vreman, A. W. & Kuerten, J. G. M. 2016 A 3-order multistep time-discretization for a chebyshev tau spectral method. J. Comput. Phys. 304, 162–169.Google Scholar