Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bhutto, Afaque Ahmed
Harijan, Khanji
Hussain, Mukkarum
Shah, Syed Feroz
and
Kumar, Laveet
2022.
Numerical Simulation of Transient Combustion and the Acoustic Environment of Obstacle Vortex-Driven Flow.
Energies,
Vol. 15,
Issue. 16,
p.
6079.
Yanaoka, Hideki
and
Nakayama, Kosuke
2022.
Numerical analysis of ligament instability and breakup in shear flow.
Physics of Fluids,
Vol. 34,
Issue. 8,
Estivalezes, J.-L.
Aniszewski, W.
Auguste, F.
Ling, Y.
Osmar, L.
Caltagirone, J.-P.
Chirco, L.
Pedrono, A.
Popinet, S.
Berlemont, A.
Magnaudet, J.
Ménard, T.
Vincent, S.
and
Zaleski, S.
2022.
A phase inversion benchmark for multiscale multiphase flows.
Journal of Computational Physics,
Vol. 450,
Issue. ,
p.
110810.
Begemann, Alexander
Trummler, Theresa
Trautner, Elias
Hasslberger, Josef
and
Klein, Markus
2022.
Effect of turbulence intensity and surface tension on the emulsification process and its stationary state—A numerical study.
The Canadian Journal of Chemical Engineering,
Vol. 100,
Issue. 12,
p.
3548.
Constante-Amores, C.R.
Chergui, J.
Shin, S.
Juric, D.
Castrejón-Pita, J.R.
and
Castrejón-Pita, A.A.
2022.
Role of surfactant-induced Marangoni stresses in retracting liquid sheets.
Journal of Fluid Mechanics,
Vol. 949,
Issue. ,
Liang, Fuyue
Kahouadji, Lyes
Valdes, Juan Pablo
Shin, Seungwon
Chergui, Jalel
Juric, Damir
and
Matar, Omar K
2022.
Numerical study of oil–water emulsion formation in stirred vessels: effect of impeller speed.
Flow,
Vol. 2,
Issue. ,
Lai, Xin
Li, Shaofan
Yan, Jiale
Liu, Lisheng
and
Zhang, A-Man
2022.
Multiphase large-eddy simulations of human cough jet development and expiratory droplet dispersion.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Constante-Amores, C.R.
Abadie, T.
Kahouadji, L.
Shin, S.
Chergui, J.
Juric, D.
Castrejón-Pita, A.A.
and
Matar, O.K.
2023.
Direct numerical simulations of turbulent jets: vortex–interface–surfactant interactions.
Journal of Fluid Mechanics,
Vol. 955,
Issue. ,
Vozhakov, Ivan S.
Hrebtov, Mikhail Yu.
Yavorsky, Nikolay I.
and
Mullyadzhanov, Rustam I.
2023.
Numerical Simulations of Swirling Water Jet Atomization: A Mesh Convergence Study.
Water,
Vol. 15,
Issue. 14,
p.
2552.
Valdes, Juan Pablo
Kahouadji, Lyes
Liang, Fuyue
Shin, Seungwon
Chergui, Jalel
Juric, Damir
and
Matar, Omar K.
2023.
On the dispersion dynamics of liquid–liquid surfactant-laden flows in a SMX static mixer.
Chemical Engineering Journal,
Vol. 475,
Issue. ,
p.
146058.
Valdes, Juan Pablo
Kahouadji, Lyes
Liang, Fuyue
Shin, Seungwon
Chergui, Jalel
Juric, Damir
and
Matar, Omar K.
2023.
Direct numerical simulations of liquid–liquid dispersions in a SMX mixer under different inlet conditions.
Chemical Engineering Journal,
Vol. 462,
Issue. ,
p.
142248.
Poblador-Ibanez, Jordi
Nocivelli, Lorenzo
Magnotti, Gina M.
Anumolu, Lakshman
and
Sforzo, Brandon A.
2023.
A physics-driven Σ-Y atomization model for heavy-duty engine simulations.
International Journal of Multiphase Flow,
Vol. 167,
Issue. ,
p.
104523.
Traverso, T.
Abadie, T.
Matar, O. K.
and
Magri, L.
2023.
Data-driven modeling for drop size distributions.
Physical Review Fluids,
Vol. 8,
Issue. 10,
Constante-Amores, C.R.
Kahouadji, L.
Shin, S.
Chergui, J.
Juric, D.
Castrejón-Pita, J.R.
Matar, O.K.
and
Castrejón-Pita, A.A.
2023.
Impact of droplets onto surfactant-laden thin liquid films.
Journal of Fluid Mechanics,
Vol. 961,
Issue. ,
Constante-Amores, C. R.
Kahouadji, L.
Williams, J. G.
Turney, B. W.
Shin, S.
Chergui, J.
Juric, D.
Moulton, D. E.
and
Waters, S. L.
2023.
Role of Kidney Stones in Renal Pelvis Flow.
Journal of Biomechanical Engineering,
Vol. 145,
Issue. 5,
Qiao, Ran
Zhao, Chengxi
Ding, Zhaodong
Mu, Kai
and
Si, Ting
2024.
Velocity modulation on the linear instability of liquid jets in ambient gas.
Physics of Fluids,
Vol. 36,
Issue. 1,
Guan, Wei
Huang, Yunlong
He, Zhixia
Guo, Genmiao
Wang, Chuqiao
and
Thévenin, Dominique
2024.
Primary breakup of a jet coupled with vortex-induced string cavitation in a fuel injector nozzle.
Physics of Fluids,
Vol. 36,
Issue. 5,
Poblador-Ibanez, Jordi
Sirignano, William A.
and
Hussain, Fazle
2024.
Vorticity dynamics in transcritical liquid jet breakup.
Journal of Fluid Mechanics,
Vol. 978,
Issue. ,
Pico, P.
Kahouadji, L.
Shin, S.
Chergui, J.
Juric, D.
and
Matar, O. K.
2024.
Drop encapsulation and bubble bursting in surfactant-laden flows in capillary channels.
Physical Review Fluids,
Vol. 9,
Issue. 3,
Montessori, Andrea
Hegele, Luiz A.
and
Lauricella, Marco
2025.
A Thread-Safe Lattice Boltzmann Model for Multicomponent Turbulent Jet Simulations.
AIAA Journal,
Vol. 63,
Issue. 3,
p.
1005.
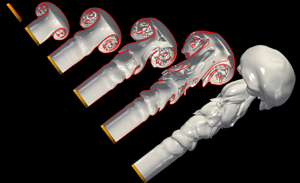
 $Re$) and Weber (
$Re$) and Weber ( $We$) numbers. We find that the interplay between the azimuthal and streamwise vorticity components leads to different interfacial features and flow regimes in
$We$) numbers. We find that the interplay between the azimuthal and streamwise vorticity components leads to different interfacial features and flow regimes in  $Re$–
$Re$– $We$ space. We show that the streamwise vorticity plays a critical role in the development of the three-dimensional instabilities on the jet surface. In the inertia-controlled regime at high
$We$ space. We show that the streamwise vorticity plays a critical role in the development of the three-dimensional instabilities on the jet surface. In the inertia-controlled regime at high  $Re$ and
$Re$ and  $We$, we expose the details of the spatio-temporal development of the vortical structures affecting the interfacial dynamics. A mushroom-like structure is formed at the leading edge of the jet inducing the generation of a liquid sheet in its interior that undergoes rupture to form droplets. These droplets rotate inside the mushroom structure due to their interaction with the prevailing vortical structures. Additionally, Kelvin–Helmholtz vortices that form near the injection point deform in the streamwise direction to form hairpin vortices, which, in turn, trigger the formation of interfacial lobes in the jet core. The thinning of the lobes induces the creation of holes which expand to form liquid threads that undergo capillary breakup to form droplets.
$We$, we expose the details of the spatio-temporal development of the vortical structures affecting the interfacial dynamics. A mushroom-like structure is formed at the leading edge of the jet inducing the generation of a liquid sheet in its interior that undergoes rupture to form droplets. These droplets rotate inside the mushroom structure due to their interaction with the prevailing vortical structures. Additionally, Kelvin–Helmholtz vortices that form near the injection point deform in the streamwise direction to form hairpin vortices, which, in turn, trigger the formation of interfacial lobes in the jet core. The thinning of the lobes induces the creation of holes which expand to form liquid threads that undergo capillary breakup to form droplets.