Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T14:43:59.312Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulations of the flow around wings with spanwise waviness

Published online by Cambridge University Press:  10 August 2017

Douglas Serson Open the ORCID record for Douglas Serson [Opens in a new window] ,
Julio R. Meneghini  and
Spencer J. Sherwin Open the ORCID record for Spencer J. Sherwin [Opens in a new window]
Douglas Serson*
Affiliation:
Department of Aeronautics, South Kensington Campus, Imperial College London, SW7 2AZ, UK NDF, Escola Politécnica, Universidade de São Paulo, Av. Prof. Mello Moraes, 2231, São Paulo, 05508-030, Brazil
Julio R. Meneghini
Affiliation:
NDF, Escola Politécnica, Universidade de São Paulo, Av. Prof. Mello Moraes, 2231, São Paulo, 05508-030, Brazil
Spencer J. Sherwin
Affiliation:
Department of Aeronautics, South Kensington Campus, Imperial College London, SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The use of spanwise waviness in wings has been proposed in the literature as a possible mechanism for obtaining improved aerodynamic characteristics, motivated by the tubercles that cover the leading edge of the pectoral flippers of the humpback whale. We investigate the effect of this type of waviness on the incompressible flow around infinite wings with a NACA0012 profile, using direct numerical simulations employing the spectral/hp method. Simulations were performed for Reynolds numbers of 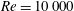$Re=10\,000$ and 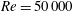$Re=50\,000$, considering different angles of attack in both the pre-stall and post-stall regimes. The results show that the waviness can either increase or decrease the lift coefficient, depending on the particular 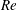$Re$ and flow regime. We observe that the flow around the wavy wing exhibits a tendency to remain attached behind the waviness peak, with separation restricted to the troughs, which is consistent with results from the literature. Then, we identify three important physical mechanisms in this flow. The first mechanism is the weakening of the suction peak on the sections corresponding to the waviness peaks. This characteristic had been observed in a previous investigation for a very low Reynolds number of 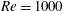$Re=1000$, and we show that this is still important even at 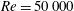$Re=50\,000$. As a second mechanism, the waviness has a significant effect on the stability of the separated shear layers, with transition occurring earlier for the wavy wing. In the pre-stall regime, for 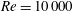$Re=10\,000$, the flow around the baseline wing is completely laminar, and the earlier transition leads to a large increase in the lift coefficient, while for 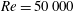$Re=50\,000$, the earlier transition leads to a shortening of the separation bubble which does not lead to an increased lift coefficient. The last mechanism corresponds to a sub-harmonic behaviour, with the flow being notably different between subsequent wavelengths. This allows the wing to maintain higher lift coefficients in some portions of the span.

JFM classification

Aerodynamics: Aerodynamics Flow Control: Flow Control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 714 - 731
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cantwell, C. D., Moxey, D., Comerford, A., Bolis, A., Rocco, G., Mengaldo, G., Grazia, D. D., Yakovlev, S., Lombard, J.-E., Ekelschot, D. et al. 2015 Nektar++: an open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.Google Scholar
Favier, J., Pinelli, A. & Piomelli, U. 2012 Control of the separated flow around an airfoil using a wavy leading edge inspired by humpback whale flippers. C. R. Méc 340, 107–114.Google Scholar
Fish, F. E. & Battle, J. M. 1995 Hydrodynamic design of the humpback whale flipper. J. Morphol. 225, 51–60.Google Scholar
Guermond, J. L. & Shen, J. 2003 Velocity-correction projection methods for incompressible flows. SIAM J. Numer. Anal. 41 (1), 112–134.Google Scholar
Hansen, K. L., Kelso, R. M. & Dally, B. B. 2010 An investigation of three-dimensional effects on the performance of tubercles at low Reynolds numbers. In 17th Australasian Fluid Mechanics Conference. University of Auckland.Google Scholar
Hansen, K. L., Kelso, R. M. & Dally, B. B. 2011 Performance variations of leading-edge tubercles for distinct airfoil profiles. AIAA J. 49 (1), 185–194.Google Scholar
Hansen, K. L., Rostamzadeh, N., Kelso, R. M. & Dally, B. B. 2016 Evolution of the streamwise vortices generated between leading edge tubercles. J. Fluid Mech. 788, 730–766.Google Scholar
Johari, H., Henoch, C., Custodio, D. & Levshin, A. 2007 Effects of leading edge protuberances on airfoil performance. AIAA J. 45 (11), 2634–2641.Google Scholar
Karniadakis, G. E. 1990 Spectral element-Fourier methods for incompressible turbulent flows. Comput. Meth. Appl. Mech. Engng 80 (1–3), 367–380.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
Karniadakis, G. E. & Sherwin, S. J. 2005 Spectral/hp Element Methods for Computational Fluid Dynamics, 2nd edn. Oxford University Press.Google Scholar
Kirby, R. M. & Sherwin, S. J. 2006a Aliasing errors due to quadratic nonlinearities on triangular spectral/hp element discretisations. J. Engng Maths 56, 273–288.CrossRefGoogle Scholar
Kirby, R. M. & Sherwin, S. J. 2006b Stabilisation of spectral/hp element methods through spectral vanishing viscosity: application to fluid mechanics modelling. Comput. Meth. Appl. Mech. Engng 195 (23–24), 3128–3144.Google Scholar
McCormick, B. W. 1995 Aerodynamics, Aeronautics, and Flight Mechanics, 2nd edn. Wiley.Google Scholar
Miklosovic, D. S., Murray, M. M. & Howle, L. E. 2007 Experimental evaluation of sinusoidal leading edges. J. Aircraft 44 (4), 1404–1407.CrossRefGoogle Scholar
Miklosovic, D. S., Murray, M. M., Howle, L. E. & Fish, F. E. 2004 Leading-edge tubercles delay stall on humpback whale (Megaptera novaeangliae) flippers. Phys. Fluids 16, L39.Google Scholar
Mueller, T. J & DeLaurier, J. D. 2003 Aerodynamics of small vehicles. Annu. Rev. Fluid Mech. 35 (1), 89–111.Google Scholar
Paula, A. A.2016 The airfoil thickness effects on wavy leading edge phenomena at low Reynolds number regime. PhD thesis, University of São Paulo.Google Scholar
Rostamzadeh, N., Hansen, K. L., Kelso, R. M. & Dally, B. B. 2014 The formation mechanism and impact of streamwise vortices on NACA 0021 airfoil’s performance with undulating leading edge modification. Phys. Fluids 26, 107101.Google Scholar
Serson, D.2017 Numerical study of wings with wavy leading and trailing edges. PhD thesis, University of São Paulo/Imperial College London.Google Scholar
Serson, D., Meneghini, J. R. & Sherwin, S. J. 2016 Velocity-correction schemes for the incompressible Navier–Stokes equations in general coordinate systems. J. Comput. Phys. 316, 243–254.Google Scholar
Serson, D., Meneghini, J. R. & Sherwin, S. J. 2017 Direct numerical simulations of the flow around wings with spanwise waviness at a very low Reynolds number. Comput. Fluids 146, 117–124.Google Scholar
Skillen, A., Revell, A., Pinelli, A., Piomelli, U. & Favier, J. 2015 Flow over a wing with leading-edge undulations. AIAA J. 53 (2), 464–472.Google Scholar
Stanway, M. J.2008 Hydrodynamic effects of leading-edge tubercles on control surfaces and in flapping foil propulsion. Master’s thesis, Massachusetts Insitute of Technology.Google Scholar