Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T18:39:03.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulations of Rayleigh–Bénard convection in water with non-Oberbeck–Boussinesq effects

Published online by Cambridge University Press:  28 October 2019

Andreas D. Demou Open the ORCID record for Andreas D. Demou [Opens in a new window]  and
Dimokratis G. E. Grigoriadis Open the ORCID record for Dimokratis G. E. Grigoriadis [Opens in a new window]
Andreas D. Demou
Affiliation:
UCY-CompSci, Department of Mechanical and Manufacturing Engineering, University of Cyprus, 1 Panepistimiou Avenue, 2109 Aglantzia, Nicosia, Cyprus
Dimokratis G. E. Grigoriadis*
Affiliation:
UCY-CompSci, Department of Mechanical and Manufacturing Engineering, University of Cyprus, 1 Panepistimiou Avenue, 2109 Aglantzia, Nicosia, Cyprus
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

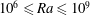Rayleigh–Bénard convection in water is studied by means of direct numerical simulations, taking into account the variation of properties. The simulations considered a three-dimensional (3-D) cavity with a square cross-section and its two-dimensional (2-D) equivalent, covering a Rayleigh number range of $10^{6}\leqslant Ra\leqslant 10^{9}$ and using temperature differences up to 60 K. The main objectives of this study are (i) to investigate and report differences obtained by 2-D and 3-D simulations and (ii) to provide a first appreciation of the non-Oberbeck–Boussinesq (NOB) effects on the near-wall time-averaged and root-mean-squared (r.m.s.) temperature fields. The Nusselt number and the thermal boundary layer thickness exhibit the most pronounced differences when calculated in two dimensions and three dimensions, even though the 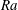$Ra$ scaling exponents are similar. These differences are closely related to the modification of the large-scale circulation pattern and become less pronounced when the NOB values are normalised with the respective Oberbeck–Boussinesq (OB) values. It is also demonstrated that NOB effects modify the near-wall temperature statistics, promoting the breaking of the top–bottom symmetry which characterises the OB approximation. The most prominent NOB effect in the near-wall region is the modification of the maximum r.m.s. values of temperature, which are found to increase at the top and decrease at the bottom of the cavity.

JFM classification

Convection: Convection in cavities Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 1073 - 1096
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G. 1980 Effect of departures from the Oberbeck–Boussinesq approximation on the heat transport of horizontal convecting fluid layers. J. Fluid Mech. 98 (1), 137–148.Google Scholar
Ahlers, G., Brown, E., Araujo, F. F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.Google Scholar
Ahlers, G., Calzavarini, E., Araujo, F. F., Funfschilling, D., Grossmann, S., Lohse, D. & Sugiyama, K. 2008 Non-Oberbeck–Boussinesq effects in turbulent thermal convection in ethane close to the critical point. Phys. Rev. E 77 (4), 046302.Google Scholar
Boussinesq, J.1903 Théorie Analytique de la Chaleur: Mise en Harmonie avec la Thermodynamique et avec la Théorie Mécanique de la Lumière, vol. 2. Gauthier-Villars.Google Scholar
Brown, E. & Ahlers, G. 2007 Temperature gradients, and search for non–Boussinesq effects, in the interior of turbulent Rayleigh–Bénard convection. Eur. Phys. Lett. 80 (1), 14001.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Demou, A. D., Frantzis, C. & Grigoriadis, D. G. E. 2018 A numerical methodology for efficient simulations of non-Oberbeck–Boussinesq flows. Intl J. Heat Mass Transfer 125, 1156–1168.Google Scholar
Demou, A. D., Frantzis, C. & Grigoriadis, D. G. E. 2019 A low-Mach methodology for efficient direct numerical simulations of variable property thermally driven flows. Intl J. Heat Mass Transfer 132, 539–549.Google Scholar
Du Puits, R., Resagk, C., Tilgner, A., Busse, F. H. & Thess, A. 2007 Structure of thermal boundary layers in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 572, 231–254.Google Scholar
Fröhlich, J., Laure, P. & Peyret, R. 1992 Large departures from Boussinesq approximation in the Rayleigh–Bénard problem. Phys. Fluids 4 (7), 1355–1372.Google Scholar
Garon, A. M. & Goldstein, R. J. 1973 Velocity and heat transfer measurements in thermal convection. Phys. Fluids 16 (11), 1818–1825.Google Scholar
Gray, D. D. & Giorgini, A. 1976 The validity of the Boussinesq approximation for liquids and gases. Intl J. Heat Mass Transfer 19 (5), 545–551.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86 (15), 3316.Google Scholar
Hiroaki, T. & Hiroshi, M. 1980 Turbulent natural convection in a horizontal water layer heated from below. Intl J. Heat Mass Transfer 23 (9), 1273–1281.Google Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26 (5), 055111.Google Scholar
Horn, S., Shishkina, O. & Wagner, C. 2013 On non-Oberbeck–Boussinesq effects in three-dimensional Rayleigh–Bénard convection in glycerol. J. Fluid Mech. 724, 175–202.Google Scholar
Kizildag, D., Rodríguez, I., Oliva, A. & Lehmkuhl, O. 2014 Limits of the Oberbeck–Boussinesq approximation in a tall differentially heated cavity filled with water. Intl J. Heat Mass Transfer 68, 489–499.Google Scholar
Liu, S., Xia, S.-N., Yan, R., Wan, Z.-H. & Sun, D.-J. 2018 Linear and weakly nonlinear analysis of Rayleigh–Bénard convection of perfect gas with non-Oberbeck–Boussinesq effects. J. Fluid Mech. 845, 141–169.Google Scholar
Manga, M. & Weeraratne, D. 1999 Experimental study of non-Boussinesq Rayleigh–Bénard convection at high Rayleigh and Prandtl numbers. Phys. Fluids 11 (10), 2969–2976.Google Scholar
Oberbeck, A. 1879 Über die Wärmeleitung der Flüssigkeiten bei Berücksichtigung der Strömungen infolge von Temperaturdifferenzen. Ann. Phys. 243 (6), 271–292.Google Scholar
van der Poel, E. P., Stevens, R. J. A. M. & Lohse, D. 2013 Comparison between two- and three-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 736, 177–194.10.1017/jfm.2013.488Google Scholar
Roy, A. & Steinberg, V. 2002 Reentrant hexagons in non-Boussinesq Rayleigh–Bénard convection: effect of compressibility. Phys. Rev. Lett. 88 (24), 244503.Google Scholar
Sebilleau, F., Issa, R., Lardeau, S. & Walker, S. P. 2018 Direct numerical simulation of an air-filled differentially heated square cavity with Rayleigh numbers up to 1011 . Intl J. Heat Mass Transfer 123, 297–319.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.Google Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2007 Non-Oberbeck–Boussinesq effects in two-dimensional Rayleigh–Bénard convection in glycerol. Eur. Phys. Lett. 80 (3), 34002.Google Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2009 Flow organization in two-dimensional non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. J. Fluid Mech. 637, 105–135.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105 (3), 034503.Google Scholar
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulent convection in water. Phys. Rev. E 47 (4), R2253.Google Scholar
Trias, F. X., Soria, M., Oliva, A. & Pérez-Segarra, C. D. 2007 Direct numerical simulations of two-and three-dimensional turbulent natural convection flows in a differentially heated cavity of aspect ratio 4. J. Fluid Mech. 586, 259–293.10.1017/S0022112007006908Google Scholar
Valori, V., Elsinga, G., Rohde, M., Tummers, M., Westerweel, J. & van der Hagen, T. 2017 Experimental velocity study of non-Boussinesq Rayleigh–Bénard convection. Phys. Rev. E 95 (5), 053113.Google Scholar
Wang, J. & Xia, K.-Q. 2003 Spatial variations of the mean and statistical quantities in the thermal boundary layers of turbulent convection. Eur. Phys. J. B 32 (1), 127–136.Google Scholar
Wang, Q., Xu, B.-L., Xia, S.-N., Wan, Z.-H. & Sun, D.-J. 2017 Thermal convection in a tilted rectangular cell with aspect ratio 0.5. Chin. Phys. Lett. 34 (10), 104401.Google Scholar
Weiss, S., He, X., Ahlers, G., Bodenschatz, E. & Shishkina, O. 2018 Bulk temperature and heat transport in turbulent Rayleigh–Bénard convection of fluids with temperature-dependent properties. J. Fluid Mech. 851, 374–390.Google Scholar
Wu, X.-Z. & Libchaber, A. 1991 Non-Boussinesq effects in free thermal convection. Phys. Rev. A 43 (6), 2833.Google Scholar
Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Intl J. Heat Mass Transfer 88 (6), 064501.Google Scholar
Zhou, Q. & Xia, K.-Q. 2013 Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell. J. Fluid Mech. 721, 199–224.Google Scholar
Zhu, X., Mathai, V., Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2018 Transition to the ultimate regime in two-dimensional Rayleigh–Bénard convection. Phys. Rev. Lett. 120 (14), 144502.Google Scholar