Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-20T08:11:06.313Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulations of low-Rm MHD turbulence based on the least dissipative modes

Published online by Cambridge University Press:  14 May 2010

ALBAN POTHÉRAT  and
VITALI DYMKOU
ALBAN POTHÉRAT*
Affiliation:
Applied Mathematics Research Centre, Faculty of Engineering and Computing, Coventry University, Coventry CV1 5FB, UK
VITALI DYMKOU
Affiliation:
Applied Mathematics Research Centre, Faculty of Engineering and Computing, Coventry University, Coventry CV1 5FB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a new spectral method for the direct numerical simulation of magnetohydrodynamic turbulence at low magnetic Reynolds number. The originality of our approach is that instead of using traditional bases of functions, it relies on the basis of eigenmodes of the dissipation operator, which represents viscous and Joule dissipation. We apply this idea to the simple case of a periodic domain in the three directions of space, with a homogeneous magnetic field in the ez direction. The basis is then still a subset of the Fourier space, but ordered by growing linear decay rate |λ| (i.e. according to the least dissipative modes). We show that because the lines of constant energy tend to follow those of constant |λ| in the Fourier space, the scaling for the smallest scales |λmax| in a forced flow can be expressed, using this single parameter, as a function of the Reynolds number as 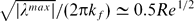, where kf is the forcing wavelength, or as a function of the Grashof number Gf, which gives a non-dimensional measure of the forcing, as |λmax|1/2/(2πkf) ≃ 0.47Gf0.20. This scaling is also found to be consistent with heuristic scalings derived by Alemany et al. (J. Mec., vol. 18, 1979, pp. 277–313) and Pothérat & Alboussière (Phys. Fluids, vol. 15, 2003, pp. 3170–3180) for interaction parameter S ≳ 1, and which we are able to numerically quantify as k⊥max/kf ≃ 0.5Re1/2 and kzmax/kf ≃ 0.8kfRe/Ha. Finally, we show that the set of least dissipative modes gives a relevant prediction for the scale of the first three-dimensional structure to appear in a forced, initially two-dimensional turbulent flow. This completes our numerical demonstration that the least dissipative modes can be used to simulate both two- and three-dimensional low-Rm magnetohydrodynamic (MHD) flows.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 655 , 25 July 2010 , pp. 174 - 197
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alemany, A., Moreau, R., Sulem, P. & Frish, U. 1979 Influence of an external magnetic field on homogeneous MHD turbulence. J. Mec. 18 (2), 277–313.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 2006 Spectral Methods: Fundamentals in Single Domains. Springer-Verlag.CrossRefGoogle Scholar
Constantin, P., Foias, C., Mannley, O. P. & Temam, R. 1985 Determining modes and fractal dimension of turbulent flows. J. Fluid. Mech. 150, 427–440.CrossRefGoogle Scholar
Davidson, P. A. 1997 The role of angular momentum in the magnetic damping of turbulence. J. Fluid Mech. 336, 123–150.CrossRefGoogle Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Delannoy, Y., Pascal, B., Alboussière, T., Uspenski, V. & Moreau, R. 1999 Quasi-two-dimensional turbulence in MHD shear flows: The Matur experiment and simulations. In Transfer Phenomena and Electroconducting Flows (ed. Alemany, A., Marty, Ph. & Thibault, J. P.). Kluwer.Google Scholar
Doering, C. R. & Gibbons, J. D. 1995 Applied Analysis of the Navier–Stokes Equation. Cambridge University Press.CrossRefGoogle Scholar
Dymkou, V. & Pothérat, A. 2009 Spectral methods based on the least dissipative modes for wall-bounded MHD flows. J. Theor. Comp. Fluid Dyn. 23 (6), 535–555.CrossRefGoogle Scholar
Foias, C., Manley, O., Rosa, R. & Temam, R. 2001 Navier–Stokes Equations and Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence, The Legacy of A.N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Klein, R. & Pothérat, A. 2010 Appearance of three-dimensionality in wall-bounded MHD flows. Phys. Rev. Lett 104 (3), 034502.CrossRefGoogle ScholarPubMed
Klein, R., Pothérat, A. & Alferjonok, A. 2009 Experiment on an electrically driven, confined vortex pair. Phys. Rev. E 79 (1), 016304.CrossRefGoogle Scholar
Knaepen, B. & Moin, P. 2004 Large-eddy simulation of conductive flows at low magnetic Reynolds number. Phys. Fluids 16 (5), 1255–1261.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 Local structure of turbulence in an incompressible fluid at very high Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kraichman, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417.CrossRefGoogle Scholar
Mininni, P. D., Alexakis, A. & Pouquet, A. 2006 Large-scale flow effects, energy transfer, and self-similarity on turbulence. Phys. Rev. E 74, 016303.CrossRefGoogle ScholarPubMed
Moffatt, H. K. 1967 On the suppression of turbulence by a uniform magnetic field. J. Fluid Mech. 28, 571–592.CrossRefGoogle Scholar
Moreau, R. 1990 Magnetohydrodynamics. Kluwer Academic Publisher.CrossRefGoogle Scholar
Nakauchi, N., Oshima, H. & Saito, Y. 1992 Two-dimensionality in low-magnetic Reynolds number magnetohydrodynamic turbulence subjected to a uniform external magnetic field and randomly stirred two-dimensional force. Phys. Fluids A 12 (4), 2906–2914.CrossRefGoogle Scholar
Ohkitani, J. 1989 Log corrected energy spectrum and attractor dimension in two-dimensional turbulence. Phys. Fluids A 1 (3), 451–452.CrossRefGoogle Scholar
Orszag, G. S. & Patterson, S. A. 1971 Spectral calculations of isotropic turbulence: efficient removal of aliasing interaction. Phys. Fluids 14, 2538–2541.Google Scholar
Pothérat, A. & Alboussière, T. 2003 Small scales and anisotropy in low-Rm magnetohydrodynamic turbulence. Phys. Fluids 15 (10), 3170–3180.CrossRefGoogle Scholar
Pothérat, A. & Alboussière, T. 2006 Bounds on the attractor dimension for low-Rm wall bound MHD turbulence. Phys. Fluids 18 (12), 125102.CrossRefGoogle Scholar
Pothérat, A., Sommeria, J. & Moreau, R. 2000 An effective two-dimensional model for MHD flows with transverse magnetic field. J. Fluid Mech. 424, 75–100.CrossRefGoogle Scholar
Roberts, P. H. 1967 Introduction to Magnetohydrodynamics. Longsmans.Google Scholar
Rogallo, R. S. 1981 Numerical Experiments in Homogeneous Turbulence. Ames Research Center, National Aeronautics and Space Administration.Google Scholar
Schumann, U. 1976 Numerical simulation of the transition from three- to two-dimensional turbulence under a uniform magnetic field. J. Fluid Mech. 35, 31–58.CrossRefGoogle Scholar
Sommeria, J. 1986 Experimental study of the two-dimensional inverse energy cascade in a square box. J. Fluid Mech. 170, 139.CrossRefGoogle Scholar
Sommeria, J. 1988 Electrically driven vortices in a strong magnetic field. J. Fluid Mech. 189, 553–569.CrossRefGoogle Scholar
Sommeria, J. & Moreau, R. 1982 Why, how and when, MHD turbulence becomes two-dimensional. J. Fluid Mech. 118, 507.CrossRefGoogle Scholar
Thess, A. & Zikanov, O. 2007 Transition from two-dimensional to three-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 579, 383–412.CrossRefGoogle Scholar
Vorobev, A, Zikanov, O., Davidson, P. A. & Knaepen, B. 2005 Anisotropy of magnetohydrodynamic turbulence at low magnetic Reynolds number. Phys. Fluids 17, 125105.CrossRefGoogle Scholar
Williamson, J. H. 1980 Low-storage Runge–Kutta schemes. J. Comp. Phys. 35, 48–56.CrossRefGoogle Scholar
Zikanov, O. & Thess, A. 1998 Direct numerical simulation of forced MHD turbulence at low magnetic Reynolds number. J. Fluid Mech. 358, 299–333.CrossRefGoogle Scholar