Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T02:47:09.114Z Has data issue: false hasContentIssue false
  • English
  • Français

A direct numerical simulation study of turbulence and flame structure in transverse jets analysed in jet-trajectory based coordinates

Published online by Cambridge University Press:  10 July 2012

R. W. Grout ,
A. Gruber ,
H. Kolla ,
P.-T. Bremer ,
J. C. Bennett ,
A. Gyulassy  and
J. H. Chen
R. W. Grout*
Affiliation:
National Renewable Energy Laboratory, Golden, CO 80401, USA
A. Gruber
Affiliation:
SINTEF Energy Research, 7465 Trondheim, Norway
H. Kolla
Affiliation:
Sandia National Laboratories, Livermore, CA 94550, USA
P.-T. Bremer
Affiliation:
Lawrence Livermore National Laboratories, Livermore, CA 94551, USA
J. C. Bennett
Affiliation:
Sandia National Laboratories, Livermore, CA 94550, USA
A. Gyulassy
Affiliation:
University of Utah, Salt Lake City, UT 84112, USA
J. H. Chen
Affiliation:
Sandia National Laboratories, Livermore, CA 94550, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An 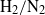jet in cross-flow (JICF) of air is studied using three-dimensional direct numerical simulation with and without chemical reaction in order to investigate the role of the complex JICF turbulent flow field in the mechanism of fast fuel-oxidant mixing and of aerodynamic flame stabilization in the near field of the jet nozzle. Focus is on delineating the flow/mixing/chemistry conditions that are necessary and/or sufficient to achieve flame anchoring that ultimately enables the formulation of more reliable and precise guidelines for design of fuel injection nozzles. A mixture averaged diffusion formulation that includes the effect of thermal diffusion is used along with a detailed chemical kinetics mechanism for hydrogen–air combustion. A new parametrization technique is used to describe the jet trajectory: solution of Laplace’s equation upon, and then within, an opportune scalar surface anchored by Dirichlet boundary conditions at the jet nozzle and plume exit from the domain provides a smoothly varying field along the jet path. The surface is selected to describe the scalar mixing and reaction associated with a transverse jet. The derived field, , is used as a condition to mark the position along the natural jet trajectory when analysing the variation of relevant flow, mixing and reaction quantities in the present direct numerical simulation (DNS) datasets. Results indicate the presence of a correlation between the flame base location in parameter space and a region of low velocity magnitude, high enstrophy, high mixing rate and high equivalence ratio (flame root region). Instantaneously, a variety of vortical structures, well known from the literature as important contributors to fuel-oxidant mixing, are observed in both inert and reactive cases with a considerable span in length scales. Moreover, instantaneous plots from reactive cases illustrate that the most upstream flame tongues propagate close to the trailing edge of the fuel jet potential core near the jet shear layer vortex shedding position. Some degree of asymmetry with respect to the domain mid-plane in the spanwise direction is observed in the averaged fields, both for the inert and reactive cases.

JFM classification

Wakes/Jets: Jets Mixing: Turbulent mixing Reacting Flows: Turbulent reacting flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 351 - 383
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Andreopoulos, J. 1985 On the structure of jets in a crossflow. J. Fluid Mech. 157, 163–197.CrossRefGoogle Scholar
2. Andreopoulos, J. & Rodi, W. 1984 Experimental investigation of jets in a crossflow. J. Fluid Mech. 138, 93–127.CrossRefGoogle Scholar
3. Ashurst, W. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30, 2343–2353.CrossRefGoogle Scholar
4. Bagheri, S., Schlatter, P., Schmid, P. J. & Henningson, D. S. 2009 Global stability of a jet in crossflow. J. Fluid Mech. 624, 33–44.CrossRefGoogle Scholar
5. Batchelor, G. K. 1959 Small scale variations of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
6. Bray, K. N. C., Domingo, P. & Vervisch, L. 2005 Role of the progress variable in models for partially premixed turbulent combustion. Combust. Flame 141, 431–437.CrossRefGoogle Scholar
7. Broadwell, J. E. & Breidenthal, R. E. 1984 Structure and mixing of a transverse jet in incompressible flow. J. Fluid Mech. 148, 405–412.CrossRefGoogle Scholar
8. Brzustowski, T. A., Gollahalli, S. R. & Sullivan, H. F. 1975 The turbulent hydrogen diffusion flame in a cross-wind. Combust. Sci. Technol. 11, 29–33.CrossRefGoogle Scholar
9. Chakraborty, N. & Swaminathan, N. 2007 Influence of the Damköhler number on turbulence–scalar interaction in premixed flames. Part 1. Physical insight. Phys. Fluids 19, 045103.Google Scholar
10. Chen, J. H., Choudhary, A., de Supinski, B., DeVries, M., Hawkes, E. R., Klasky, S., Liao, W. K., Ma, K. L., Mellor-Crummey, J., Podhorski, N., Sankaran, R., Shende, S. & Yoo, C. S. 2009 Terascale direct numerical simulations of turbulent combustion using S3D. Comput. Sci. Disc. 2, 1–31.CrossRefGoogle Scholar
11. Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2 (5), 765–777.CrossRefGoogle Scholar
12. Coelho, S. L. V. & Hunt, J. C. R. 1989 The dynamics of the near field of strong jets in crossflows. J. Fluid Mech. 200, 95–120.CrossRefGoogle Scholar
13. Cortelezzi, L. & Karagozian, A. R. 2001 On the formation of the counter-rotating vortex pair in transverse jets. J. Fluid Mech. 446, 347–373.CrossRefGoogle Scholar
14. Demmel, J. W., Eisenstat, S. C., Gilbert, J. R., Li, X. S. & Liu, J. W. H. 1999 A supernodal approach to sparse partial pivoting. SIAM J. Matrix Anal. Appl. 20 (3), 720–755.CrossRefGoogle Scholar
15. Döbbeling, K., Hellat, J. & Koch, H. 2007 25 years of BBC/ABB/Alstom lean premix combustion technologies. ASME J. Engng for Gas Turbines and Power 129, 2–12.CrossRefGoogle Scholar
16. Echekki, T. & Chen, J. H. 2003 Direct numerical simulation of autoignition in non-homogeneous hydrogen–air mixtures. Combust. Flame 134, 169–191.CrossRefGoogle Scholar
17. Fearn, R. & Weston, R. 1974 Vorticity associated with a jet in a cross flow. AIAA J. 12, 1666–1671.CrossRefGoogle Scholar
18. Fearn, R. L. & Weston, R. P. 1975 Induced pressure distribution of a jet in a crossflow. Tech. Rep. TN-D7916. NASA, Langley Research Center.Google Scholar
19. Fearn, R. L. & Weston, R. P. 1978 Induced velocity field of a jet in a crossflow. Tech. Rep. TP-1087. NASA, Langley Research Center.Google Scholar
20. Fearn, R. L. & Weston, R. P. 1979 Velocity field of a round jet in a cross flow for various jet injection angles and velocity ratios. Tech. Rep. TP-1506. NASA, Langley Research Center.Google Scholar
21. Floater, M. & Hormann, K. 2005 Surface parameterization: a tutorial and survey. In Adv. Multiresolution for Geometric Modelling, pp. 157–186. Springer.CrossRefGoogle Scholar
22. Fric, T. F. & Roshko, A. 1994 Vortical structure in the wake of a transverse jet. J. Fluid Mech. 279, 1–47.Google Scholar
23. Galeazzo, F. C. C., Donnert, G., Habisreuther, P., Zarzalis, N., Valdes, R. J. & Krebs, W. 2011 Measurements and simulation of turbulent mixing in a jet in crossflow. ASME J. Engng Gas Turbines and Power 133, 061504.CrossRefGoogle Scholar
24. Garland, M. & Heckbert, P. S. 1997 Surface simplification using quadric error metrics. In Proceedings of the 24th Annual Conference on Computer graphics and Interactive Techniques: SIGGRAPH’97, pp. 209–216. Association for Computing Machinery, Inc. (ACM).CrossRefGoogle Scholar
25. Gibson, C. H. 1968 Fine structure of scalar fields mixed by turbulence. Part 1. Zero gradient points and minimal gradient surfaces. Phys. Fluids 11, 2305.CrossRefGoogle Scholar
26. Gollahalli, S. R. & Pardiwalla, D. 2002 Comparison of the flame characteristics of turbulent circular and elliptic jets in a crossflow. ASME J. Energy Resour. Technol. 124, 197–203.CrossRefGoogle Scholar
27. Grout, R. W., Gruber, A., Yoo, C. S. & Chen, J. H. 2011 Direct numerical simulation of flame stabilization downstream of a transverse fuel jet in cross-flow. Proc. Combust. Inst. 33 (1), 1629–1637.Google Scholar
28. Gruber, A., Sankaran, R., Hawkes, E. R. & Chen, J. H. 2010 Turbulent flame–wall interaction: a direct numerical simulation study. J. Fluid Mech. 658, 5–32.CrossRefGoogle Scholar
29. Gutmark, E. J., Ibrahim, I. M. & Murugappan, S. 2008 Circular and noncircular subsonic jets in cross flow. Phys. Fluids 20, 075110.CrossRefGoogle Scholar
30. Hasselbrink, E. F. & Mungal, M. G. 2001a Transverse jets and jet flames. Part 1. Scaling laws for strong transverse jets. J. Fluid Mech. 443, 1–25.CrossRefGoogle Scholar
31. Hasselbrink, E. F. & Mungal, M. G. 2001b Transverse jets and jet flames. Part 2. Velocity and OH field imaging. J. Fluid Mech. 443, 27–68.CrossRefGoogle Scholar
32. Haven, B. A. & Kurosaka, M. 1997 Kidney and anti-kidney vortices in crossflow jets. J. Fluid Mech. 352, 27–64.Google Scholar
33. Hawkes, E. R. & Chen, J. H. 2005 Evaluation of models for flame stretch due to curvature in the thin reaction zones regime. In 30th International Symposium on Combustion, pp. 647–655. The Combustion Institute.Google Scholar
34. Hawkes, E. R., Sankaran, R., Sutherland, J. C. & Chen, J. H. 2007 Scalar mixing in direct numerical simulations of temporally evolving plane jet flames with skeletal CO/ kinetics. In 31st International Symposium on Combustion, pp. 1633–1640. The Combustion Institute.Google Scholar
35. Holdeman, J. D. 1972 Correlation for temperature profiles in the plane of symmetry downstream of a jet injected normal to a crossflow. Tech. Rep. TN-D6966. NASA, Lewis Research Center.Google Scholar
36. Jessen, W., Schröder, W. & Klaas, M. 2007 Evolution of jets effusing from inclined holes into crossflow. Intl J. Heat Fluid Flow 28, 1312–1326.Google Scholar
37. Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.CrossRefGoogle Scholar
38. Karagozian, A. R. 2010 Transverse jets and their control. Prog. Energy Combust. Sci. 36, 531–553.Google Scholar
39. Kee, R. J., Dixon-Lewis, G., Warnatz, J., Coltrin, M. E., Miller, J. A. & Moffat, H. K. 1999 A Fortran chemical kinetics package for the analysis of gas-phase chemical kinetics. Tech. Rep. Release 3.5. Reaction Design Inc., San Diego, CA.Google Scholar
40. Kelso, R. M., Lim, T. T. & Perry, A. E. 1996 An experimental study of round jets in crossflow. J. Fluid Mech. 306, 111–144.CrossRefGoogle Scholar
41. Kennedy, C. A. & Carpenter, M. H. 1994 Several new numerical methods for compressible shear-layer simulations. Appl. Numer. Math. 14 (4), 397–433.CrossRefGoogle Scholar
42. Kennedy, C. A., Carpenter, M. H. & Lewis, R. M. 2000 Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations. Appl. Numer. Math. 35 (3), 177–219.Google Scholar
43. Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.Google Scholar
44. Li, J., Zhao, Z., Kazarov, A. & Dryer, F. L. 2004 An updated comprehensive kinetic model of hydrogen combustion. Intl J. Chem. Kinet. 36, 566–575.CrossRefGoogle Scholar
45. Lorensen, W. E. & Cline, H. E. 1987 Marching cubes: a high resolution 3D surface construction algorithm. Comput. Graph. 21 (4), 163–169.CrossRefGoogle Scholar
46. Lu, T. F., Yoo, C. S., Chen, J. H. & Law, C. K. 2010 Three-dimensional direct numerical simulation of a turbulent lifted hydrogen jet flame in heated coflow: a chemical explosive mode analysis. J. Fluid Mech. 652, 45–64.CrossRefGoogle Scholar
47. Lund, T. S., Squires, K. D. & Wu, X. 2003 Turbulent inflow boundary conditions for LES. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, 6–9 January 2003, Reno, Nevada. American Institute of Aeronautics and Astronautics.Google Scholar
48. Moser, R., Kim, J. & Mansour, N. 1999 Direct numerical simulation of turbulent channel flow up to . Phys. Fluids 11 (4), 943–945.CrossRefGoogle Scholar
49. Mount, D. M. 2010 ANN Programming Manual. http://www.cs.umd.edu/~mount/ANN/Files/1.1.2/ANNmanual_1.1.pdf.Google Scholar
50. Muppidi, S. & Mahesh, K. 2005 Study of trajectories of jets in crossflow using direct numerical simulations. J. Fluid Mech. 530, 81–100.CrossRefGoogle Scholar
51. Muppidi, S. & Mahesh, K. 2008 Direct numerical simulation of passive scalar transport in transverse jets. J. Fluid Mech. 598, 335–360.CrossRefGoogle Scholar
52. New, T. H., Lim, T. T. & Luo, S. C. 2006 Effects of jet velocity profiles on a round jet in cross-flow. Exp. Fluids 40, 859–875.CrossRefGoogle Scholar
53. Oberlack, M., Arlitt, R. & Peters, N. 2000 On stochastic Damköhler number variations in a homogeneous flow reactor. Combust. Theor. Model. 4 (4), 495–509.Google Scholar
54. Passot, T. & Pouquet, A. 1987 Numerical simulation of compressible homogeneous flows in the turbulent regime. J. Fluid Mech. 181, 441–466.CrossRefGoogle Scholar
55. Pitsch, H. & Fedotov, S. 2001 Investigation of scalar dissipation rate fluctuations in non-premixed turbulent combustion using a stochastic approach. Combust. Theor. Model. 5 (1), 41–57.CrossRefGoogle Scholar
56. Poinsot, T. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flow. J. Comput. Phys. 101, 104–129.Google Scholar
57. Poinsot, T. & Veynante, D. 2001 Theoretical and Numerical Combustion, first edition. Edwards.Google Scholar
58. Poinsot, T., Veynante, D., Trouvé, A. & Ruetsch, G. R. 1996 Turbulent flame propagation in partially premixed flames. CTR Summer Program 1996.Google Scholar
59. Salewski, M., Stankovic, D. & Fuchs, L. 2008 Mixing in circular and non-circular jets in crossflow. Flow Turbul. Combust. 80, 255–283.CrossRefGoogle Scholar
60. Sankaran, R., Hawkes, E. R., Chen, J. H., Lu, T. & Law, C. K. 2007 Structure of a spatially developing turbulent lean methane–air Bunsen flame. In 31st International Symposium on Combustion, pp. 1291–1298. The Combustion Institute.Google Scholar
61. Sankaran, R., Im, H. G., Hawkes, E. R. & Chen, J. H. 2005 The effects of non-uniform temperature distribution on the ignition of a lean homogeneous hydrogen–air mixture. In 30th International Symposium on Combustion, pp. 875–882. The Combustion Institute.Google Scholar
62. Schmitt, D. A. 1985 Radiation from a hydrogen flare in crosswind. In Proceedings of the 23rd AIAA Meeting, pp. AIAA–1985–0153. American Institute of Aeronautics and Astronautics.Google Scholar
63. Si, H. 2011 TetGen: A Quality Tetrahedral Mesh Generator and a 3D Delaunay Triangulator, first edition. Weierstrass Institute for Applied Analysis and Stochastics (WIAS).Google Scholar
64. Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228, 4218–4231.CrossRefGoogle Scholar
65. Smith, S. H. & Mungal, M. G. 1998 Mixing, structure and scaling of the jet in crossflow. J. Fluid Mech. 357, 83–122.Google Scholar
66. Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to . J. Fluid Mech. 187, 61–98.CrossRefGoogle Scholar
67. Su, L. K. & Mungal, M. G. 2004 Simultaneous measurements of scalar and velocity field evolution in turbulent crossflowing jets. J. Fluid Mech. 513, 1–45.CrossRefGoogle Scholar
68. Sutherland, J. C. & Kennedy, C. A. 2003 Improved boundary conditions for viscous, reactive, compressible flows. J. Comput. Phys. 191, 502–524.CrossRefGoogle Scholar
69. Swaminathan, N. & Bilger, R. W. 1997 Direct numerical simulation of turbulent nonpremixed hydrocarbon reaction zones using a two-step reduced mechanism. Combust. Sci. Technol. 127, 167–196.CrossRefGoogle Scholar
70. Swaminathan, N. & Grout, R. W. 2006 Interaction of turbulence and scalar fields in premixed flames. Phys. Fluids 18 (4).CrossRefGoogle Scholar
71. Taubin, G. 1995 A signal processing approach to fair surface design. In SIGGRAPH, pp. 351–358.Google Scholar
72. Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
73. Veynante, D. & Vervisch, L. 2002 Turbulent combustion modeling. Prog. Energy Combust. Sci. 28, 193–266.CrossRefGoogle Scholar
74. Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.Google Scholar
75. Yoo, C. S., Sankaran, R. & Chen, J. H. 2009 Three-dimensional direct numerical simulation of a turbulent lifted hydrogen jet flame in heated coflow: flame stabilization and structure. J. Fluid Mech. 640, 453–481.CrossRefGoogle Scholar