Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
MacDonald, M.
Chan, L.
Chung, D.
Hutchins, N.
and
Ooi, A.
2016.
Turbulent flow over transitionally rough surfaces with varying roughness densities.
Journal of Fluid Mechanics,
Vol. 804,
Issue. ,
p.
130.
Jing, He-fang
Li, Yi-tian
and
Li, Chun-guang
2016.
Numerical study of the flow in the Yellow River with non-monotonous banks.
Journal of Hydrodynamics,
Vol. 28,
Issue. 1,
p.
142.
Abderrahaman-Elena, Nabil
and
García-Mayoral, Ricardo
2017.
Analysis of anisotropically permeable surfaces for turbulent drag reduction.
Physical Review Fluids,
Vol. 2,
Issue. 11,
Di Natale, F.
Orefice, M.
La Motta, F.
Erto, A.
and
Lancia, A.
2017.
Unveiling the potentialities of activated carbon in recovering palladium from model leaching solutions.
Separation and Purification Technology,
Vol. 174,
Issue. ,
p.
183.
Samanta, Arghya
2017.
Role of slip on the linear stability of a liquid flow through a porous channel.
Physics of Fluids,
Vol. 29,
Issue. 9,
Rosti, Marco E.
and
Brandt, Luca
2017.
Numerical simulation of turbulent channel flow over a viscous hyper-elastic wall.
Journal of Fluid Mechanics,
Vol. 830,
Issue. ,
p.
708.
Lācis, Uǧis
and
Bagheri, Shervin
2017.
A framework for computing effective boundary conditions at the interface between free fluid and a porous medium.
Journal of Fluid Mechanics,
Vol. 812,
Issue. ,
p.
866.
Suga, Kazuhiko
Nakagawa, Yuka
and
Kaneda, Masayuki
2017.
Spanwise turbulence structure over permeable walls.
Journal of Fluid Mechanics,
Vol. 822,
Issue. ,
p.
186.
Terekhov, V. V.
and
Terekhov, V. I.
2017.
Effect of surface permeability on the structure of a separated turbulent flow and heat transfer behind a backward-facing step.
Journal of Applied Mechanics and Technical Physics,
Vol. 58,
Issue. 2,
p.
254.
Yang, Guang
Weigand, Bernhard
Terzis, Alexandros
Weishaupt, Kilian
and
Helmig, Rainer
2018.
Numerical Simulation of Turbulent Flow and Heat Transfer in a Three-Dimensional Channel Coupled with Flow Through Porous Structures.
Transport in Porous Media,
Vol. 122,
Issue. 1,
p.
145.
Gómez-de-Segura, G.
Sharma, A.
and
García-Mayoral, R.
2018.
Turbulent Drag Reduction Using Anisotropic Permeable Substrates.
Flow, Turbulence and Combustion,
Vol. 100,
Issue. 4,
p.
995.
Efstathiou, Christoph
and
Luhar, Mitul
2018.
Mean turbulence statistics in boundary layers over high-porosity foams.
Journal of Fluid Mechanics,
Vol. 841,
Issue. ,
p.
351.
Rosti, Marco E.
Brandt, Luca
and
Pinelli, Alfredo
2018.
Turbulent channel flow over an anisotropic porous wall – drag increase and reduction.
Journal of Fluid Mechanics,
Vol. 842,
Issue. ,
p.
381.
Suga, Kazuhiko
Okazaki, Yuki
Ho, Unde
and
Kuwata, Yusuke
2018.
Anisotropic wall permeability effects on turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 855,
Issue. ,
p.
983.
De Vita, F.
Rosti, M.E.
Izbassarov, D.
Duffo, L.
Tammisola, O.
Hormozi, S.
and
Brandt, L.
2018.
Elastoviscoplastic flows in porous media.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 258,
Issue. ,
p.
10.
Showkat Ali, Syamir Alihan
Azarpeyvand, Mahdi
Szőke, Máté
and
Ilário da Silva, Carlos Roberto
2018.
Boundary layer flow interaction with a permeable wall.
Physics of Fluids,
Vol. 30,
Issue. 8,
Rosti, Marco E.
and
Brandt, Luca
2018.
Suspensions of deformable particles in a Couette flow.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 262,
Issue. ,
p.
3.
Rosti, Marco E.
Izbassarov, Daulet
Tammisola, Outi
Hormozi, Sarah
and
Brandt, Luca
2018.
Turbulent channel flow of an elastoviscoplastic fluid.
Journal of Fluid Mechanics,
Vol. 853,
Issue. ,
p.
488.
Dritselis, Chris D.
Tzorbatzoglou, Fotini
Mastrokalos, Marios
and
Haralampous, Onoufrios
2019.
Numerical Study of Flow and Particle Deposition in Wall-Flow Filters with Intact or Damaged Exit.
Fluids,
Vol. 4,
Issue. 4,
p.
201.
Ghosh, Souvik
Loiseau, Jean-Christophe
Breugem, Wim-Paul
and
Brandt, Luca
2019.
Modal and non-modal linear stability of Poiseuille flow through a channel with a porous substrate.
European Journal of Mechanics - B/Fluids,
Vol. 75,
Issue. ,
p.
29.
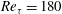 $Re_{{\it\tau}}=180$ and consider low-permeability materials; a parameter study is used to describe the role played by permeability, porosity, thickness of the porous material, and the coefficient of the momentum-transfer interface conditions. Among them permeability, even when very small, is shown to play a major role in determining the response of the channel flow to the permeable wall. Turbulence statistics and instantaneous flow fields, in comparative form to the flow over a smooth impermeable wall, are used to understand the main changes introduced by the porous material. A simulation at higher Reynolds number is used to illustrate the main scaling quantities.
$Re_{{\it\tau}}=180$ and consider low-permeability materials; a parameter study is used to describe the role played by permeability, porosity, thickness of the porous material, and the coefficient of the momentum-transfer interface conditions. Among them permeability, even when very small, is shown to play a major role in determining the response of the channel flow to the permeable wall. Turbulence statistics and instantaneous flow fields, in comparative form to the flow over a smooth impermeable wall, are used to understand the main changes introduced by the porous material. A simulation at higher Reynolds number is used to illustrate the main scaling quantities.