Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T04:34:05.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of turbulence over systematically varied irregular rough surfaces

Published online by Cambridge University Press:  25 January 2019

Y. Kuwata Open the ORCID record for Y. Kuwata [Opens in a new window]  and
Y. Kawaguchi
Y. Kuwata*
Affiliation:
Department of Mechanical Engineering, Osaka Prefecture University, Sakai, Osaka, 599-8531, Japan
Y. Kawaguchi
Affiliation:
Department of Mechanical Engineering, Tokyo University of Science, 2641 Yamazaki, Noda, Chiba 278-8510, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Lattice Boltzmann direct numerical simulation of turbulent open-channel flows over randomly distributed hemispheres at 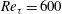$Re_{\unicode[STIX]{x1D70F}}=600$ is carried out to reveal the influence of roughness parameters related to a probability density function of rough-surface elevation on turbulence by analysing the spatial and Reynolds- (double-) averaged Navier–Stokes equation. This study specifically concentrates on the influence of the root-mean-square roughness and the skewness, and profiles of turbulence statistics are compared by introducing an effective wall-normal distance defined as a wall-normal integrated plane porosity. The effective distance can completely collapse the total shear stress outside the roughness sublayer, and thus the similarity of the streamwise mean velocity is clearer by introducing the effective distance. In order to examine the influence of the root-mean-square roughness and the skewness on dynamical effects that contribute to an increase in the skin friction coefficient, the triple-integrated double-averaged Navier–Stokes equation is analysed. The main contributors to the skin friction coefficient are found to be turbulence and drag force. The turbulence contribution increases with the root-mean-square roughness and/or the skewness. The drag force contribution, on the other hand, increases in particular with the root-mean-square roughness whereas an increase in the skewness does not increase the drag force contribution because it does not necessarily increase the surface area of the roughness elements. The contribution of the mean velocity dispersion induced by spatial inhomogeneity of the rough surfaces substantially increases with the root-mean-square roughness. A linear correlation is confirmed between the root-mean-square roughness and the equivalent roughness while the equivalent roughness monotonically increases with the skewness. A new correlation function based on the root-mean-square roughness and the skewness is developed with the available experimental and direct numerical simulation data, and it is confirmed that the developed correlation reasonably predicts the equivalent roughness of various types of real rough surfaces.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 781 - 815
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acharya, M., Bornstein, J. & Escudier, M. P. 1986 Turbulent boundary layers on rough surfaces. Exp. Fluids 4 (1), 33–47.Google Scholar
Ashrafian, A., Andersson, H. I. & Manhart, M. 2004 DNS of turbulent flow in a rod-roughened channel. Intl J. Heat Fluid Flow 25 (3), 373–383.Google Scholar
Aupoix, B. & Spalart, P. R. 2003 Extensions of the spalart–allmaras turbulence model to account for wall roughness. Intl J. Heat Fluid Flow 24 (4), 454–462.Google Scholar
Beugre, D., Sbastien, C., Grard, D., Michel, C., Dominique, T. & Pierre, M. 2010 Lattice Boltzmann 3D flow simulations on a metallic foam. J. Comput. Appl. Maths 234 (7), 2128–2134.Google Scholar
Bespalko, D., Pollard, A. & Uddin, M. 2012 Analysis of the pressure fluctuations from an LBM simulation of turbulent channel flow. Comput. Fluids 54, 143–146.Google Scholar
Bhaganagar, K. & Chau, L. 2015 Characterizing turbulent flow over 3-D idealized and irregular rough surfaces at low Reynolds number. Appl. Math. Model. 39 (22), 6751–6766.Google Scholar
Bhaganagar, K., Kim, J. & Coleman, G. 2004 Effect of roughness on wall-bounded turbulence. Flow Turbul. Combust. 72 (2–4), 463–492.Google Scholar
Bons, J. P. 2002 St and Cf augmentation for real turbine roughness with elevated freestream turbulence. In ASME Turbo Expo 2002: Power for Land, Sea, and Air, pp. 349–363. American Society of Mechanical Engineers.Google Scholar
Bons, J. P. 2005 A critical assessment of Reynolds analogy for turbine flows. Trans. ASME J. Heat Transfer 127 (5), 472–485.Google Scholar
Bons, J. P. 2010 A review of surface roughness effects in gas turbines. Trans. ASME J. Turbomach. 132 (2), 021004.Google Scholar
Bons, J. P., Taylor, R. P., McClain, S. T. & Rivir, R. B. 2001 The many faces of turbine surface roughness. Trans. ASMEJ. Turbomach. 123, 739–748.Google Scholar
Busse, A., Lützner, M. & Sandham, N. D. 2015 Direct numerical simulation of turbulent flow over a rough surface based on a surface scan. Comput. Fluids 116, 129–147.Google Scholar
Busse, A., Thakkar, M. & Sandham, N. D. 2017 Reynolds-number dependence of the near-wall flow over irregular rough surfaces. J. Fluid Mech. 810, 196–224.Google Scholar
Cardillo, J., Chen, Y., Araya, G., Newman, J., Jansen, K. & Castillo, L. 2013 DNS of a turbulent boundary layer with surface roughness. J. Fluid Mech. 729, 603–637.Google Scholar
Chan, L., MacDonald, M., Chung, D., Hutchins, N. & Ooi, A. 2015 A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 771, 743–777.Google Scholar
Chatzikyriakou, D., Buongiorno, J., Caviezel, D. & Lakehal, D. 2015 DNS and LES of turbulent flow in a closed channel featuring a pattern of hemispherical roughness elements. Intl J. Heat Fluid Flow 53, 29–43.Google Scholar
Cheng, H. & Castro, I. P. 2002 Near wall flow over urban-like roughness. Boundary-Layer Meteorol. 104 (2), 229–259.Google Scholar
Chikatamarla, S. S., Frouzakis, C. E., Karlin, I. V., Tomboulides, A. G. & Boulouchos, K. B. 2010 Lattice Boltzmann method for direct numerical simulation of turbulent flows. J. Fluid Mech. 656, 298–308.Google Scholar
Chukwudozie, C. & Tyagi, M. 2013 Pore scale inertial flow simulations in 3-D smooth and rough sphere packs using lattice Boltzmann method. AIChE J. 59, 4858–4870.Google Scholar
Colebrook, C. F., Blench, T., Chatley, H., Essex, E. H., Finniecome, J. R., Lacey, G., Williamson, J. & MacDonald, G. G. 1939 Correspondence turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws (include plates). J. Inst. Civil Engrs Lond. 12 (8), 393–422.Google Scholar
Coleman, H. W., Hodge, B. K. & Taylor, R. P. 1984 A re-evaluation of Schlichting’s surface roughness experiment. Trans. ASME J. Fluids Engng 106, 60–65.Google Scholar
De Marchis, M., Napoli, E. & Armenio, V. 2010 Turbulence structures over irregular rough surfaces. J. Turbul. 11 (3), 1–32.Google Scholar
d’Humiéres, D., Ginzburg, I., Krafczyk, M., Lallemand, P. & Luo, L.-S. 2002 Multiple-relaxation-time lattice Boltzmann models in three dimensions. Phil. Trans. R. Soc. Lond. A 360, 437–451.Google Scholar
Dirling, R. B.1973 A method for computing roughwall heat transfer rates on reentry nosetips. AIAA Paper 73–763.Google Scholar
Durbin, P. A., Medic, G., Seo, J.-M., Eaton, J. K. & Song, S. 2001 Rough wall modification of two-layer k-𝜀. J. Fluids Engng 123 (1), 16–21.Google Scholar
Dvorak, F. A. 1969 Calculation of turbulent boundary layers on rough surfaces in pressure gradient. AIAA J. 7 (9), 1752–1759.Google Scholar
Fattahi, E., Waluga, C., Wohlmuth, B., Rüde, U., Manhart, M. & Helmig, R. 2016 Lattice Boltzmann methods in porous media simulations: from laminar to turbulent flow. Comput. Fluids 140, 247–259.Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32, 519–571.Google Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19 (9), 095104.Google Scholar
Flack, K. A & Schultz, M. P. 2010 Review of hydraulic roughness scales in the fully rough regime. Trans. ASME J. Fluids Engng 132 (4), 041203.Google Scholar
Flack, K. A., Schultz, M. P., Barros, J. M. & Kim, Y. C. 2016 Skin-friction behavior in the transitionally-rough regime. Intl J. Heat Fluid Flow 61, 21–30.Google Scholar
Flack, K. A., Schultz, M. P. & Rose, W. B. 2012 The onset of roughness effects in the transitionally rough regime. Intl J. Heat Fluid Flow 35, 160–167.Google Scholar
Forooghi, P., Stroh, A., Magagnato, F., Jakirlić, S. & Frohnapfel, B. 2017 Toward a universal roughness correlation. Trans. ASME J. Fluids Engng 139 (12), 121201.Google Scholar
Forooghi, P., Stroh, A., Schlatter, P. & Frohnapfel, B. 2018a Direct numerical simulation of flow over dissimilar, randomly distributed roughness elements: a systematic study on the effect of surface morphology on turbulence. Phys. Rev. Fluids 3 (4), 044605.Google Scholar
Forooghi, P., Weidenlener, A., Magagnato, F., Böhm, B., Kubach, H., Koch, T. & Frohnapfel, B. 2018b DNS of momentum and heat transfer over rough surfaces based on realistic combustion chamber deposit geometries. Intl J. Heat Fluid Flow 69, 83–94.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), L73–L76.Google Scholar
Gehrke, M., Janßen, C. F. & Rung, T. 2017 Scrutinizing lattice Boltzmann methods for direct numerical simulations of turbulent channel flows. Comput. Fluids 156, 247–263.Google Scholar
Hama, F. R. 1954 Boundary layer characteristics for smooth and rough surfaces. Trans. Soc. Nav. Archit. Mar. Engrs 62, 333–358.Google Scholar
Hasert, M., Bernsdorf, J. & Roller, S. 2011 Lattice Boltzmann simulation of non-Darcy flow in porous media. Procedia Comput. Sci. 4, 1048–1057.Google Scholar
Hatiboglu, C. U. & Babadagli, T. 2008 Pore-scale studies of spontaneous imbibition into oil-saturated porous media. Phys. Rev. E 77, 066311.Google Scholar
He, X. & Luo, L.-S. 1997 Lattice Boltzmann model for the incompressible Navier–Stokes equation. J. Stat. Phys. 88 (3–4), 927–944.Google Scholar
Howell, D. & Behrends, B. 2006 A review of surface roughness in antifouling coatings illustrating the importance of cutoff length. Biofouling 22 (6), 401–410.Google Scholar
Huang, C., Shi, B., He, N. & Chai, Z. 2015 Implementation of Multi-GPU based lattice Boltzmann method for flow through porous media. Adv. Appl. Math. Mech. 7 (1), 1–12.Google Scholar
Ikeda, T. & Durbin, P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.Google Scholar
Iwamoto, K., Suzuki, Y. & Kasagi, N.2002 Database of fully developed channel flow-thtlab internal report no. ILR-0201, Rapport technique, THTLAB, Dept. of Mech. Engng., The Univ. of Tokyo.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Jin, Y., Uth, M. F. & Herwig, H. 2015 Structure of a turbulent flow through plane channels with smooth and rough walls: an analysis based on high resolution DNS results. Comput. Fluids 107, 77–88.Google Scholar
Kang, S. K. & Hassan, Y. A. 2013 The effect of lattice models within the lattice Boltzmann method in the simulation of wall-bounded turbulent flows. J. Comput. Phys. 232 (1), 100–117.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kirschner, C. M. & Brennan, A. B. 2012 Bio-inspired antifouling strategies. Annu. Rev. Mater. Res. 42, 211–229.Google Scholar
Krafczyk, M., Kucher, K., Wang, Y. & Geier, M. 2015 DNS/LES studies of turbulent flows based on the cumulant lattice Boltzmann approach. In High Performance Computing in Science and Engineering 14, pp. 519–531. Springer.Google Scholar
Krogstad, P.-Å, Andersson, H. I., Bakken, O. M. & Ashrafian, A. 2005 An experimental and numerical study of channel flow with rough walls. J. Fluid Mech. 530, 327–352.Google Scholar
Kuwata, Y. & Kawaguchi, Y. 2017 Lattice Boltzmann direct numerical simulation of turbulence over resolved and modelled rough walls with irregularly distributed roughness. Intl J. Heat Fluid Flow; (submitted).Google Scholar
Kuwata, Y. & Kawaguchi, Y. 2018 Statistical discussions on skin frictional drag of turbulence over randomly distributed semi-spheres. Intl J. Adv. Engng Sci. Appl. Maths 10 (4), 263–272.Google Scholar
Kuwata, Y. & Suga, K. 2015a Anomaly of the lattice Boltzmann methods in three-dimensional cylindrical flows. J. Comput. Phys. 280, 563–569.Google Scholar
Kuwata, Y. & Suga, K. 2015b Large eddy simulations of pore-scale turbulent flows in porous media by the lattice Boltzmann method. Intl J. Heat Fluid Flow 55, 143–157.Google Scholar
Kuwata, Y. & Suga, K. 2016a Imbalance-correction grid-refinement method for lattice Boltzmann flow simulations. J. Comput. Phys. 311, 348–362.Google Scholar
Kuwata, Y. & Suga, K. 2016b Lattice Boltzmann direct numerical simulation of interface turbulence over porous and rough walls. Intl J. Heat Fluid Flow 61, 145–157.Google Scholar
Kuwata, Y. & Suga, K. 2016c Transport mechanism of interface turbulence over porous and rough walls. Flow Turbul. Combust. 97 (4), 1071–1093.Google Scholar
Kuwata, Y. & Suga, K. 2017 Direct numerical simulation of turbulence over anisotropic porous media. J. Fluid Mech. 831, 41–71.Google Scholar
Lammers, P., Beronov, K. N., Volkert, R., Brenner, G. & Durst, F. 2006 Lattice BGK direct numerical simulation of fully developed turbulence in incompressible plane channel flow. Comput. Fluids 35 (10), 1137–1153.Google Scholar
Langelandsvik, L. I., Kunkel, G. J. & Smits, A. J. 2008 Flow in a commercial steel pipe. J. Fluid Mech. 595, 323–339.Google Scholar
Lee, J. H., Sung, H. J. & Krogstad, P.-Å. 2011 Direct numerical simulation of the turbulent boundary layer over a cube-roughened wall. J. Fluid Mech. 669, 397–431.Google Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.Google Scholar
Ligrani, P. M. & Moffat, R. J. 1986 Structure of transitionally rough and fully rough turbulent boundary layers. J. Fluid Mech. 162, 69–98.Google Scholar
MacDonald, M., Chan, L., Chung, D., Hutchins, N. & Ooi, A. 2016 Turbulent flow over transitionally rough surfaces with varying roughness densities. J. Fluid Mech. 804, 130–161.Google Scholar
Miyake, Y., Tsujimoto, K. & Nakaji, M. 2001 Direct numerical simulation of rough-wall heat transfer in a turbulent channel flow. Intl J. Heat Fluid Flow 22 (3), 237–244.Google Scholar
Moody, L. F. 1944 Friction factors for pipe flow. Trans. ASME 66 (8), 671–684.Google Scholar
Musker, A. J. 1980 Universal roughness functions for naturally-occurring surfaces. Trans. Can. Soc. Mech. Engng 6 (1), 1–6.Google Scholar
Nagano, Y., Hattori, H. & Houra, T. 2004 Dns of velocity and thermal fields in turbulent channel flow with transverse-rib roughness. Intl J. Heat Fluid Flow 25 (3), 393–403.Google Scholar
Napoli, E., Armenio, V. & De Marchis, M. 2008 The effect of the slope of irregularly distributed roughness elements on turbulent wall-bounded flows. J. Fluid Mech. 613, 385–394.Google Scholar
Nikuradse, J. 1933 Laws of flow in rough pipes. In VDI Forschungsheft. Citeseer.Google Scholar
Orlandi, P. 2013 The importance of wall-normal Reynolds stress in turbulent rough channel flows. Phys. Fluids 25 (11), 110813.Google Scholar
Orlandi, P. & Leonardi, S. 2008 Direct numerical simulation of three-dimensional turbulent rough channels: parameterization and flow physics. J. Fluid Mech. 606, 399–415.Google Scholar
Parmigiani, A., Huber, C., Bachmann, O. & Chopard, B. 2011 Pore-scale mass and reactant transport in multiphase porous media flows. J. Fluid Mech. 686, 40–76.Google Scholar
Perry, A. E. & Li, J. D. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.Google Scholar
Raupach, M. R. 1994a Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Boundary-Layer Meteorol. 71 (1–2), 211–216.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.Google Scholar
Raupach, M. R. 1994b Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Boundary-Layer Meteorol. 71, 211–216.Google Scholar
Schlichting, H., Gersten, K., Krause, E., Oertel, H. & Mayes, K. 1955 Boundary-Layer Theory, vol. 7. Springer.Google Scholar
Schultz, M. P., Bendick, J. A., Holm, E. R. & Hertel, W. M. 2011 Economic impact of biofouling on a naval surface ship. Biofouling 27 (1), 87–98.Google Scholar
Schultz, M. P. & Flack, K. A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21 (1), 015104.Google Scholar
Shockling, M. A., Allen, J. J. & Smits, A. J. 2006 Roughness effects in turbulent pipe flow. J. Fluid Mech. 564, 267–285.Google Scholar
Sigal, A. & Danberg, J. E. 1990 New correlation of roughness density effect on the turbulent boundary layer. AIAA J. 28 (3), 554–556.Google Scholar
Suga, K., Kuwata, Y., Takashima, K. & Chikasue, R. 2015 A D3Q27 multiple-relaxation-time lattice Boltzmann method for turbulent flows. Comput. Math. Appl. 69, 518–529.Google Scholar
Suga, K. & Nishio, Y. 2009 Three dimensional microscopic flow simulation across the interface of a porous wall and clear fluid by the lattice Boltzmann method. Open Transp. Phenom. J. 1, 35–44.Google Scholar
Suga, K., Tanaka, T., Nishio, Y. & Murata, M. 2009 A boundary reconstruction scheme for lattice Boltzmann flow simulation in porous media. Prog. Comput. Fluid Dyn. 9, 201–207.Google Scholar
Thakkar, M., Busse, A. & Sandham, N. D. 2017 Surface correlations of hydrodynamic drag for transitionally rough engineering surfaces. J. Turbul. 18 (2), 138–169.Google Scholar
Tóth, G. & Jánosi, I. M. 2015 Vorticity generation by rough walls in 2D decaying turbulence. J. Stat. Phys. 161 (6), 1508–1518.Google Scholar
Townsin, R. L. 2003 The ship hull fouling penalty. Biofouling 19 (S1), 9–15.Google Scholar
Townsin, R. L., Byrne, D., Svensen, T. E. & Milne, A. 1981 Estimating the technical and economic penalties of hull and propeller roughness. Trans. SNAME 89, 295–318.Google Scholar
Van Rij, Jennifer, A., Belnap, B. J. & Ligrani, P. M. 2002 Analysis and experiments on three-dimensional, irregular surface roughness. Trans. ASME J. Fluids Engng 124 (3), 671–677.Google Scholar
Wahl, M. 1989 Marine epibiosis. i. fouling and antifouling: some basic aspects. Mar. Ecol. Prog. Ser. 58, 175–189.Google Scholar
Wang, P., Wang, L.-P. & Guo, Z. 2016 Comparison of the lattice Boltzmann equation and discrete unified gas-kinetic scheme methods for direct numerical simulation of decaying turbulent flows. Phys. Rev. E 94 (4), 043304.Google Scholar
Whitaker, S. 1986 Flow in porous media I. A theoretical derivation of Darcy’s law. Trans. Porous Med. 1, 3–25.Google Scholar
White, A. T. & Chong, C. K. 2011 Rotational invariance in the three-dimensional lattice Boltzmann method is dependent on the choice of lattice. J. Comput. Phys. 230 (16), 6367–6378.Google Scholar
Xipeng, L., Yun, Z., Xiaowei, W. & Wei, G. 2013 GPU-based numerical simulation of multi-phase flow in porous media using multiple-relaxation-time lattice Boltzmann method. Chem. Engng Sci. 102, 209–219.Google Scholar
Yuan, J. & Piomelli, U. 2014 Estimation and prediction of the roughness function on realistic surfaces. J. Turbul. 15 (6), 350–365.Google Scholar