Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Berk, Tim
and
Coletti, Filippo
2023.
Dynamics and scaling of particle streaks in high-Reynolds-number turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 975,
Issue. ,
Zhang, Huan
Cui, Yuankai
and
Zheng, Xiaojing
2023.
How electrostatic forces affect particle behaviour in turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 967,
Issue. ,
Jing, Siyu
Duan, Yanchong
and
Li, Danxun
2023.
A quantitative study on the turbulent kinetic energy redistribution in the near free-water-surface region of open channel flows.
AIP Advances,
Vol. 13,
Issue. 3,
Chiarini, Alessandro
and
Rosti, Marco Edoardo
2024.
Finite-size inertial spherical particles in turbulence.
Journal of Fluid Mechanics,
Vol. 988,
Issue. ,
Yu, Ming
Zhao, Lihao
Yuan, Xianxu
and
Xu, Chunxiao
2024.
Transport of inertial spherical particles in compressible turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 990,
Issue. ,
Grace, Andrew P.
Richter, David H.
and
Bragg, Andrew D.
2024.
A Reinterpretation of Phenomenological Modeling Approaches for Lagrangian Particles Settling in a Turbulent Boundary Layer.
Boundary-Layer Meteorology,
Vol. 190,
Issue. 4,
Sofiadis, George
Liakopoulos, Antonios
Palasis, Apostolos
and
Sofos, Filippos
2024.
Turbulent Micropolar Open-Channel Flow.
Fluids,
Vol. 9,
Issue. 9,
p.
202.
Wei, Qingqing
Wang, Ping
and
Zheng, Xiaojing
2024.
Modulations of turbulent/non-turbulent interfaces by particles in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 983,
Issue. ,
Gao, Wei
Shi, Pengyu
Parsani, Matteo
and
Costa, Pedro
2024.
On the relevance of lift force modelling in turbulent wall flows with small inertial particles.
Journal of Fluid Mechanics,
Vol. 988,
Issue. ,
Gao, Wei
Wang, Minmiao
and
Parsani, Matteo
2024.
Drag modulation by inertial particles in a drag-reduced turbulent channel flow with spanwise wall oscillation.
Physics of Fluids,
Vol. 36,
Issue. 10,
Van Doren, Jonathan S.
and
Kasbaoui, M. Houssem
2024.
Turbulence modulation in dense liquid-solid channel flow.
Physical Review Fluids,
Vol. 9,
Issue. 6,
Li, Jinchi
Wang, Ping
and
Zheng, Xiaojing
2024.
Effects of the Saffman lift force on particle statistics and turbulence modulation in two-phase flow.
Physical Review Fluids,
Vol. 9,
Issue. 3,
Xu, Ao
Xu, Ben-Rui
and
Xi, Heng-Dong
2024.
Particle transport and deposition in wall-sheared thermal turbulence.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Feng, Yuen
Liu, Hongyou
and
Zheng, Xiaojing
2024.
The modulation of coherent structures by the near-wall motions of particles.
Journal of Fluid Mechanics,
Vol. 981,
Issue. ,
Cui, Yuankai
Zhang, Huan
and
Zheng, Xiaojing
2024.
Turbulence modulation by charged inertial particles in channel flow.
Journal of Fluid Mechanics,
Vol. 990,
Issue. ,
Tao, Shi
Zhang, Xilin
Wang, Wenhao
Wu, Hao
Wang, Liang
and
He, Qing
2025.
Moving multiblock lattice Boltzmann simulations of fluid-particle flows.
Physics of Fluids,
Vol. 37,
Issue. 3,
Gao, Wei
Wang, Minmiao
and
Parsani, Matteo
2025.
Direct numerical simulation of particle-laden turbulent channel flow over superhydrophobic surfaces.
Physics of Fluids,
Vol. 37,
Issue. 3,
Yu, Ming
Du, Yibin
Wang, Qian
Dong, Siwei
and
Yuan, Xianxu
2025.
Two-way momentum and thermal coupling particle-laden compressible turbulent boundary layers.
Physical Review Fluids,
Vol. 10,
Issue. 2,
Wang, Ping
Chen, Zhizong
Jin, Nan
and
Zheng, Xiaojing
2025.
Wall model for large eddy simulations accounting for particle effect.
International Journal of Multiphase Flow,
Vol. 186,
Issue. ,
p.
105152.
Grace, Andrew P.
and
Richter, David
2025.
Multi-scale interactions in turbulent mixed convection drive efficient transport of Lagrangian particles.
Journal of Fluid Mechanics,
Vol. 1008,
Issue. ,
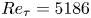 $Re_{\tau }=5186$
$Re_{\tau }=5186$
 $Re_{\tau }$) of 5186, which exhibits many characteristics of high-Reynolds-number wall-bounded turbulence, such as the distinct separation of scales in the inner and outer layers. Three representative cases, an unladen case and low- and high-Stokes-number particle-laden cases, are performed to investigate the turbulent modification by particles. To this end, we compare several statistical quantities to understand the particle effect on momentum exchange and interphasial energy transfer. The modulation of large-scale motions (LSMs) and very-large-scale motions (VLSMs) are analysed using spectral information, and we find that the LSMs and VLSMs are generally weakened in the inner and outer layers, which is qualitatively different from similar simulations at lower Reynolds numbers (
$Re_{\tau }$) of 5186, which exhibits many characteristics of high-Reynolds-number wall-bounded turbulence, such as the distinct separation of scales in the inner and outer layers. Three representative cases, an unladen case and low- and high-Stokes-number particle-laden cases, are performed to investigate the turbulent modification by particles. To this end, we compare several statistical quantities to understand the particle effect on momentum exchange and interphasial energy transfer. The modulation of large-scale motions (LSMs) and very-large-scale motions (VLSMs) are analysed using spectral information, and we find that the LSMs and VLSMs are generally weakened in the inner and outer layers, which is qualitatively different from similar simulations at lower Reynolds numbers ( $Re_{\tau } \approx 500$). The spatial structures are investigated with correlation analysis, and inclined VLSMs are observed in the near-wall region, with decreased inclination angles by particles. The particles tend to widen and shorten the spanwise and streamwise extent of coherent structures, respectively. Furthermore, we find that the vorticity vector displays a preferential alignment with the eigenvector corresponding to the intermediate eigenvalue of the strain-rate tensor, independent of the particle Stokes number.
$Re_{\tau } \approx 500$). The spatial structures are investigated with correlation analysis, and inclined VLSMs are observed in the near-wall region, with decreased inclination angles by particles. The particles tend to widen and shorten the spanwise and streamwise extent of coherent structures, respectively. Furthermore, we find that the vorticity vector displays a preferential alignment with the eigenvector corresponding to the intermediate eigenvalue of the strain-rate tensor, independent of the particle Stokes number.