Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T09:19:48.378Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of low-Reynolds-number flow past arrays of rotating spheres

Published online by Cambridge University Press:  22 January 2015

Qiang Zhou  and
Liang-Shih Fan
Qiang Zhou
Affiliation:
Department of Chemical and Biomolecular Engineering, The Ohio State University, Columbus, OH 43210, USA
Liang-Shih Fan*
Affiliation:
Department of Chemical and Biomolecular Engineering, The Ohio State University, Columbus, OH 43210, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Immersed boundary-lattice Boltzmann simulations are used to examine the effects of particle rotation, at low particle Reynolds numbers, on flows in ordered and random arrays of mono-disperse spheres. The drag force, the Magnus lift force and the torque on the spheres, are determined at solid volume fractions up to the close-packed limits of the arrays. The rotational Reynolds number based on the angular velocity and the diameter of the spheres is used to characterize the rotational movement of spheres. The results show that the normalized Magnus lift force produced by particle rotation is approximately in direct proportion to the rotational Reynolds number, while the normalized drag force and torque acting on spheres are barely affected by this number. The Magnus lift force is negligible relative to the magnitude of the drag force when the rotational Reynolds number is low. 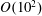However, it can be very significant, and even larger than the drag force, as the rotational Reynolds number increases up to $O(10^{2})$, especially for low solid volume fractions. Based on the simulation results, relations for the Magnus lift force and the torque for both ordered arrays and random arrays of rotating spheres at solid volume fractions from zero to close-packed limits are formulated. Further, the drag force relations in the literature are revised based on existing theories and the present simulation results for both arrays of spheres.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 765 , 25 February 2015 , pp. 396 - 423
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. D. 2005 Ludwig Prandtl’s boundary layer. Phys. Today 58 (12), 42–48.CrossRefGoogle Scholar
Bagchi, P. & Balachandar, S. 2002 Effect of free rotation on the motion of a solid sphere in linear shear flow at moderate $Re$ . Phys. Fluids 14, 2719–2737.CrossRefGoogle Scholar
Bagnold, R. A. 1973 The nature of saltation and of ‘bedload’ transport in water. Proc. R. Soc. Lond. A 332, 473–504.Google Scholar
Barkla, H. M. & Auchterlonie, L. J. 1971 The Magnus or Robins effect on rotating spheres. J. Fluid Mech. 47, 437–447.CrossRefGoogle Scholar
Breugem, W. P. 2012 A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231, 4469–4498.CrossRefGoogle Scholar
Carman, P. C. 1937 Fluid flow through a granular bed. Trans. Inst. Chem. Engrs Lond. 15, 150–156.Google Scholar
Crowe, C., Schwarzkopf, J. D., Sommerfeld, M. & Tsuji, Y. 2012 Multiphase Flows with Droplets and Particles, 2nd edn. CRC Press.Google Scholar
Dandy, D. & Dwyer, H. A. 1990 A sphere in linear shear flow at finite Reynolds number: effect of shear on particle lift, drag, and heat transfer. J. Fluid Mech. 216, 381–410.CrossRefGoogle Scholar
Dennis, S. C. R., Singh, S. N. & Ingham, D. B. 1980 The steady flow due to a rotating sphere at low and moderate Reynolds numbers. J. Fluid Mech. 101, 257–279.CrossRefGoogle Scholar
Goldschmidt, M.2001 Hydrodynamic modelling of fluidised bed spray granulation. PhD thesis, Twente University, Netherlands.Google Scholar
Hasimoto, H. 1959 On the periodic fundamental solution of the Stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5, 317–328.CrossRefGoogle Scholar
Hill, R. J., Koch, D. L. & Ladd, A. J. C. 2001a The first effects of fluid inertia on flows in ordered and random arrays of spheres. J. Fluid Mech. 448, 213–241.CrossRefGoogle Scholar
Hill, R. J., Koch, D. L. & Ladd, A. J. C. 2001b Moderate-Reynolds-number flows in ordered and random arrays of spheres. J. Fluid Mech. 448, 243–278.CrossRefGoogle Scholar
Jenkins, J. T. & Zhang, C. 2002 Kinetic theory for identical, frictional, nearly elastic spheres. Phys. Fluids 14 (3), 1228–1235.CrossRefGoogle Scholar
Kang, L. & Zou, X. Y. 2011 Vertical distribution of wind-sand interaction forces in aeolian sand transport. Geomorphology 125, 361–373.CrossRefGoogle Scholar
Kim, S. & Russel, W. B. 1985 Modelling of porous media by renormalization of the Stokes equation. J. Fluid Mech. 154, 269–286.CrossRefGoogle Scholar
Kirchhoff, G. 1876 Vorlesungen uber Mathematische Physik: Mechanik. Teubner.Google Scholar
Koch, D. L. & Sangani, A. S. 1999 Particle pressure and marginal stability limits for homogeneous monodisperse gas fluidized bed: kinetic theory and numerical simulations. J. Fluid Mech. 400, 229–263.CrossRefGoogle Scholar
Kriebitzsch, S. H. L., Van der Hoef, M. A. & Kuipers, J. A. M. 2013 Drag force in discrete particle models – continuum scale or single particle scale? AIChE J. 59 (1), 316–324.CrossRefGoogle Scholar
Kurose, R. & Komori, S. 1999 Drag and lift forces on a rotating sphere in a linear shear flow. J. Fluid Mech. 384, 183–206.CrossRefGoogle Scholar
Ladd, A. J. C. 1988 Hydrodynamic interactions in a suspension of spherical particles. J. Chem. Phys. 88, 5051–5063.CrossRefGoogle Scholar
Ladd, A. J. C. 1990 Hydrodynamic transport coefficients of random dispersions of hard spheres. J. Chem. Phys. 93, 3484–3494.CrossRefGoogle Scholar
Ladd, A. J. C. 1994 Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 271, 311–339.CrossRefGoogle Scholar
Loth, E. 2008 Lift of a solid spherical particle subject to vorticity and/or spin. AIAA J. 46 (4), 801–809.CrossRefGoogle Scholar
Lun, C. K. K. 1991 Kinetic theory for granular flow of dense, slightly inelastic, slightly rough, spheres. J. Fluid Mech. 233, 539–559.CrossRefGoogle Scholar
Lun, C. K. K. & Liu, H. S. 1997 Numerical simulation of dilute turbulent gas–solid flows in horizontal channels. Intl J. Multiphase Flow 23, 575–605.CrossRefGoogle Scholar
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. 1953 Equation of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1092.CrossRefGoogle Scholar
Oesterle, B. & Dinh, T. B. 1998 Experiments on the lift of a spinning sphere in a range of intermediate Reynolds numbers. Exp. Fluids 25, 16–22.Google Scholar
Rice, J. A. 1995 Mathematical Statistics and Data Analysis, 2nd edn. Duxbury Press.Google Scholar
Rubinow, S. I. & Keller, J. B. 1961 The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 11 (3), 447–459.CrossRefGoogle Scholar
Saffman, P. G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22, 385–400.CrossRefGoogle Scholar
Sangani, A. S. & Acrivos, A. 1982 Slow flow through a periodic array of spheres. Intl J. Multiphase Flow 8, 343–360.CrossRefGoogle Scholar
Schellander, D., Schneiderbauer, S. & Pirker, S. 2013 Numerical study of dilute and dense poly-dispersed gas–solid two-phase flows using an Eulerian and Lagrangian hybrid model. Chem. Engng Sci. 95, 107–118.CrossRefGoogle Scholar
Scott, G. D. & Kilgour, D. M. 1969 The density of random close packing of spheres. Brit. J. Appl. Phys. 2 (2), 863–866.Google Scholar
Shaffer, F., Shadle, L. & Breault, R.2009 High speed particle imaging: visualization and measurement of high concentration particle flow. In US Department of Energy National Energy Technology Laboratory (NETL) Multiphase Flow Workshop, Morgantown, WV, April 22–23.Google Scholar
Sun, J. & Battaglia, F. 2006 Hydrodynamic modeling of particle rotation for segregation in bubbling gas-fluidized beds. Chem. Engng Sci. 61, 1470–1479.CrossRefGoogle Scholar
Takagi, H. 1977 Viscous flow induced by slow rotation of a sphere. J. Phys. Soc. Japan 42, 319–325.CrossRefGoogle Scholar
Tenneti, S., Garg, R. & Subramaniam, S. 2011 Drag law for monodisperse gas–solid systems using particle-resolved direct numerical simulation of flow past fixed assemblies of spheres. Intl J. Multiphase Flow 37, 1072–1092.CrossRefGoogle Scholar
Tenneti, S. & Subramaniam, S. 2014 Particle-resolved direct numerical simulation for gas–solid flow model development. Annu. Rev. Fluid Mech. 46, 199–230.CrossRefGoogle Scholar
Tsuji, Y., Kawaguchi, T. & Tanaka, T. 1993 Discrete particle simulation of 2-dimensional fluidized-bed. Powder Technol. 77, 79–87.CrossRefGoogle Scholar
Tsuji, Y., Morikawa, Y. & Mizuno, O. 1985 Experimental measurement of the Magnus force on a rotating sphere at low Reynolds numbers. Trans. ASME: J. Fluids Engng 107, 484–488.Google Scholar
Tsuji, Y., Morikawa, Y., Tanaka, T., Nakatsukasa, N. & Nakatani, M. 1987 Numerical simulation of gas–solid two-phase flow in a two-dimensional horizontal channel. Intl J. Multiphase Flow 13 (5), 671–684.CrossRefGoogle Scholar
Tsuji, Y., Tanaka, T. & Ishida, T. 1992 Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 71, 239–250.CrossRefGoogle Scholar
Van der Hoef, M. A., Beetstra, R. & Kuipers, J. A. M. 2005 Lattice-Boltzmann simulations of low-Reynolds-number flow past mono- and bidisperse arrays of spheres: results for the permeability and drag force. J. Fluid Mech. 528, 233–254.CrossRefGoogle Scholar
Wang, S., Hao, Z., Lu, H., Yang, Y., Xu, P. & Liu, G. 2012 Hydrodynamic modeling of particle rotation in bubbling gas-fluidized beds. Intl J. Multiphase Flow 39, 159–178.Google Scholar
Wen, C. Y. & Yu, Y. H. 1966 Mechanics of fluidization. Chem. Engng Symp. Ser. 62, 100–111.Google Scholar
White, B. R. 1982 Two-phase measurements of saltating turbulent boundary layer flow. Intl J. Multiphase Flow 8, 459–473.CrossRefGoogle Scholar
White, B. R. & Schulz, J. C. 1977 Magnus effect in saltation. J. Fluid Mech. 81, 497–512.CrossRefGoogle Scholar
Wu, X., Wang, Q., Luo, Z., Fang, M. & Cen, K. 2008 Experimental study of particle rotation characteristics with high-speed digital imaging system. Powder Technol. 181, 21–30.CrossRefGoogle Scholar
Xu, B. H. & Yu, A. B. 1997 Numerical simulation of the gas–solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics. Chem. Engng Sci. 52, 2785–2809.CrossRefGoogle Scholar
Xu, B. H. & Yu, A. B. 1998 Comments on the paper ‘Numerical simulation of the gas–solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics’ – reply. Chem. Engng Sci. 53, 2646–2647.Google Scholar
Xu, M., Chen, F., Liu, X., Ge, W. & Li, J. 2012 Discrete particle simulation of gas–solid two-phase flows with multi-scale CPU-GPU hybrid computation. Chem. Engng J. 207–208, 746–757.CrossRefGoogle Scholar
Zhou, G., Xiong, Q., Wang, L., Wang, X., Ren, X & Ge, W. 2014 Structure-dependent drag in gas–solid flows studied with direct numerical simulation. Chem. Engng Sci. 116, 9–22.CrossRefGoogle Scholar
Zhou, Q. & Fan, L. S. 2014 A second-order accurate immersed boundary-lattice Boltzmann method for particle-laden flows. J. Comput. Phys. 268, 269–301.CrossRefGoogle Scholar
Zhu, H. P., Zhou, Z. Y., Yang, R. Y. & Yu, A. B. 2007 Discrete particle simulation of particulate systems: theoretical developments. Chem. Engng Sci. 62, 3378–3392.CrossRefGoogle Scholar
Zick, A. A. & Homsy, G. M. 1982 Stokes flow through periodic arrays of spheres. J. Fluid Mech. 115, 13–26.CrossRefGoogle Scholar
Zinchenko, A. Z. 1994 Algorithm for random close packing of spheres with periodic boundary conditions. J. Comput. Phys. 114, 298–306.CrossRefGoogle Scholar
Zou, L. M., Guo, Y. C. & Chan, C. K. 2008 Cluster-based drag coefficient model for simulating gas–solid flow in a fast-fluidized bed. Chem. Engng Sci. 63, 1052–1061.CrossRefGoogle Scholar
Zou, X. Y., Cheng, H., Zhang, C. L. & Zhao, Y. Z. 2007 Effects of the Magnus and Saffman forces on the saltation trajectories of sand grain. Geomorphology 90, 11–22.CrossRefGoogle Scholar