Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2025-01-04T04:22:23.980Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of high aspect ratio spanwise-aligned bars

Published online by Cambridge University Press:  19 March 2018

M. MacDonald Open the ORCID record for M. MacDonald [Opens in a new window] ,
A. Ooi ,
R. García-Mayoral ,
N. Hutchins  and
D. Chung Open the ORCID record for D. Chung [Opens in a new window]
M. MacDonald*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
A. Ooi
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
R. García-Mayoral
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
N. Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
D. Chung
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

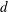We conduct minimal-channel direct numerical simulations of turbulent flow over two-dimensional rectangular bars aligned in the spanwise direction. This roughness has often been described as $d$-type, as the roughness function 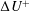$\unicode[STIX]{x0394}U^{+}$ is thought to depend only on the outer-layer length scale (pipe diameter, channel half-height or boundary layer thickness). This is in contrast to conventional engineering rough surfaces, named 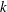$k$-type, for which 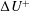$\unicode[STIX]{x0394}U^{+}$ depends on the roughness height, 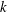$k$. The minimal-span rough-wall channel is used to circumvent the high cost of simulating high Reynolds number flows, enabling a range of bars with varying aspect ratios to be investigated. The present results show that increasing the trough-to-crest height, 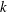$k$, of the roughness while keeping the width between roughness bars, 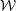${\mathcal{W}}$, fixed in viscous units, results in non-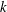$k$-type behaviour although this does not necessarily indicate 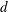$d$-type behaviour. Instead, for deep surfaces with 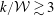$k/{\mathcal{W}}\gtrsim 3$, the roughness function appears to depend only on 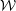${\mathcal{W}}$ in viscous units. In these situations, the flow no longer has any information about how deep the roughness is and instead can only ‘see’ the width of the fluid gap between the bars.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 126 - 155
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrose, H. H. 1956 The Effect of Character of Surface Roughness on Velocity Distribution and Boundary Resistance. The University of Tennessee College of Engineering.Google Scholar
Böhm, M., Finnigan, J. J., Raupach, M. R. & Hughes, D. 2013 Turbulence structure within and above a canopy of bluff elements. Boundary-Layer Meteorol. 146, 393–419.Google Scholar
Busse, A., Thakkar, M. & Sandham, N. D. 2017 Reynolds-number dependence of the near-wall flow over irregular rough surfaces. J. Fluid Mech. 810, 196–224.10.1017/jfm.2016.680Google Scholar
Castro, I. P. 2017 Are urban-canopy velocity profiles exponential? Boundary-Layer Meteorol. 164, 337–351.10.1007/s10546-017-0258-xGoogle Scholar
Castro, I. P., Xie, Z.-T., Fuka, V., Robins, A. G., Carpentieri, M., Hayden, P., Hertwig, D. & Coceal, O. 2017 Measurements and computations of flow in an urban street system. Boundary-Layer Meteorol. 162, 207–230.10.1007/s10546-016-0200-7Google Scholar
Chan, L., MacDonald, M., Chung, D., Hutchins, N. & Ooi, A. 2015 A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 771, 743–777.10.1017/jfm.2015.172Google Scholar
Cheng, M. & Hung, K. C. 2006 Vortex structure of steady flow in a rectangular cavity. Comput. Fluids 35 (10), 1046–1062.10.1016/j.compfluid.2005.08.006Google Scholar
Chung, D., Chan, L., MacDonald, M., Hutchins, N. & Ooi, A. 2015 A fast direct numerical simulation method for characterising hydraulic roughness. J. Fluid Mech. 773, 418–431.Google Scholar
Coleman, S. E., Nikora, V. I., McLean, S. R. & Schlicke, E. 2007 Spatially averaged turbulent flow over square ribs. J. Engng Mech. ASCE 133 (2), 194–204.10.1061/(ASCE)0733-9399(2007)133:2(194)Google Scholar
Cui, J., Patel, V. C. & Lin, C.-L. 2003 Large-eddy simulation of turbulent flow in a channel with rib roughness. Intl J. Heat Fluid Flow 24 (3), 372–388.10.1016/S0142-727X(03)00002-XGoogle Scholar
Djenidi, L., Elavarasan, R. & Antonia, R. A. 1999 The turbulent boundary layer over transverse square cavities. J. Fluid Mech. 395, 271–294.10.1017/S0022112099005911Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.10.1146/annurev.fluid.32.1.519Google Scholar
Flack, K. A. & Schultz, M. P. 2014 Roughness effects on wall-bounded turbulent flows. Phys. Fluids 26, 101305.10.1063/1.4896280Google Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19, 095104.10.1063/1.2757708Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.Google Scholar
García-Mayoral, R. & Jiménez, J. 2011 Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 678, 317–347.10.1017/jfm.2011.114Google Scholar
Ghisalberti, M. & Nepf, H. M. 2004 The limited growth of vegetated shear layers. Water Resour. Res. 40, W07502.10.1029/2003WR002776Google Scholar
Ham, F. & Iaccarino, G. 2004 Energy conservation in collocated discretization schemes on unstructured meshes. In Annual Research Briefs 2004, pp. 3–14. Center for Turbulence Research, Stanford University/NASA Ames.Google Scholar
Hama, F. R. 1954 Boundary-layer characteristics for smooth and rough surfaces. Trans. Soc. Nav. Archit. Mar. Engrs 62, 333–358.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.10.1017/S0022112095000978Google Scholar
Hunter, L. J., Johnson, G. T. & Watson, I. D. 1992 An investigation of three-dimensional characteristics of flow regimes within the urban canyon. Atmos. Environ. 26 (4), 425–432.10.1016/0957-1272(92)90049-XGoogle Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.10.1017/S0022112081002279Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.10.1017/S0022112096003965Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.10.1146/annurev.fluid.36.050802.122103Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.10.1017/S0022112091002033Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.10.1017/S0022112067001740Google Scholar
Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.10.1017/S0022112003004695Google Scholar
Leonardi, S. & Castro, I. P. 2010 Channel flow over large cube roughness: a direct numerical simulation study. J. Fluid Mech. 651, 519–539.10.1017/S002211200999423XGoogle Scholar
Leonardi, S., Orlandi, P. & Antonia, R. A. 2007 Properties of d- and k-type roughness in a turbulent channel flow. Phys. Fluids 19, 125101.10.1063/1.2821908Google Scholar
Luchini, P., Manzo, F. & Pozzi, A. 1991 Resistance of a grooved surface to parallel flow and cross-flow. J. Fluid Mech. 228, 87–109.Google Scholar
MacDonald, M., Chan, L., Chung, D., Hutchins, N. & Ooi, A. 2016 Turbulent flow over transitionally rough surfaces with varying roughness density. J. Fluid Mech. 804, 130–161.Google Scholar
MacDonald, M., Chung, D., Hutchins, N., Chan, L., Ooi, A. & García-Mayoral, R. 2017 The minimal-span channel for rough-wall turbulent flows. J. Fluid Mech. 816, 5–42.10.1017/jfm.2017.69Google Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197, 215–240.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.10.1063/1.3006423Google Scholar
Nepf, H., Ghisalberti, M., White, B. & Murphy, E. 2007 Retention time and dispersion associated with submerged aquatic canopies. Water Resour. Res. 43, W04422.10.1029/2006WR005362Google Scholar
Nepf, H. M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.10.1146/annurev-fluid-120710-101048Google Scholar
Nikuradse, J.1933 Laws of flow in rough pipes. English translation published 1950, NACA Tech. Mem. 1292.Google Scholar
Patil, D. V., Lakshmisha, K. N. & Rogg, B. 2006 Lattice Boltzmann simulation of lid-driven flow in deep cavities. Comput. Fluids 35 (10), 1116–1125.10.1016/j.compfluid.2005.06.006Google Scholar
Perry, A. E., Schofield, W. H. & Joubert, P. N. 1969 Rough wall turbulent boundary layers. J. Fluid Mech. 37 (2), 383–413.10.1017/S0022112069000619Google Scholar
Poggi, D. & Katul, G. G. 2008 The effect of canopy roughness density on the constitutive components of the dispersive stresses. Exp. Fluids 45, 111–121.10.1007/s00348-008-0467-7Google Scholar
Poggi, D., Katul, G. G. & Albertson, J. D. 2004 A note on the contribution of dispersive fluxes to momentum transfer within canopies. Boundary-Layer Meteorol. 111, 615–621.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.10.1115/1.3119492Google Scholar
Raupach, M. R., Finnigan, J. J. & Brunet, Y. 1996 Coherent eddies and turbulence in vegetation canopies: the mixing-layer analogy. Boundary-Layer Meteorol. 78, 351–382.10.1007/BF00120941Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.10.1017/S0022112072000679Google Scholar
Sadique, J., Yang, X. I. A., Meneveau, C. & Mittal, R. 2017 Aerodynamic properties of rough surfaces with high aspect-ratio roughness elements: effect of aspect ratio and arrangements. Boundary-Layer Meteorol. 163, 203–224.10.1007/s10546-016-0222-1Google Scholar
Saito, N., Pullin, D. I. & Inoue, M. 2012 Large eddy simulation of smooth-wall, transitional and fully rough-wall channel flow. Phys. Fluids 24, 075103.10.1063/1.4731301Google Scholar
Sams, E. W.1952 Experimental investigation of average heat-transfer and friction coefficients for air flowing in circular tubes having square-thread-type roughness. NACA Research Mem. E52D17.Google Scholar
Seo, J. & Mani, A. 2016 On the scaling of the slip velocity in turbulent flows over superhydrophobic surfaces. Phys. Fluids 28, 025110.10.1063/1.4941769Google Scholar
Streeter, V. L. & Chu, H.1949 Fluid flow and heat transfer in artificially roughneed pipes. Final Report, Project 4918. Armour Research Foundation, Illinois.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Yang, X. I. A., Sadique, J., Mittal, R. & Meneveau, C. 2016 Exponential roughness layer and analytical model for turbulent boundary layer flow over rectangular-prism roughness elements. J. Fluid Mech. 789, 127–165.10.1017/jfm.2015.687Google Scholar