Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T22:40:45.271Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of a turbulent hydraulic jump: turbulence statistics and air entrainment

Published online by Cambridge University Press:  16 May 2016

Milad Mortazavi ,
Vincent Le Chenadec Open the ORCID record for Vincent Le Chenadec [Opens in a new window] ,
Parviz Moin  and
Ali Mani
Milad Mortazavi
Affiliation:
Center for Turbulence Research Stanford University, Stanford, CA 94305, USA
Vincent Le Chenadec
Affiliation:
Center for Turbulence Research Stanford University, Stanford, CA 94305, USA
Parviz Moin
Affiliation:
Center for Turbulence Research Stanford University, Stanford, CA 94305, USA
Ali Mani*
Affiliation:
Center for Turbulence Research Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present direct numerical simulation (DNS) of a stationary turbulent hydraulic jump with inflow Froude number of 2, Weber number of 1820 and density ratio of 831, consistent with ambient water–air systems, all based on the inlet height and inlet velocity. A non-dissipative geometric volume of fluid (VOF) method is used to track the detailed interactions between turbulent flow structures and the nonlinear interface dynamics. Level set equations are also solved concurrent with VOF in order to calculate the interface curvature and surface tension forces. The mesh resolution is set to resolve a wide range of interfacial scales including the Hinze scale. Calculations are compared against experimental data of void fraction and interfacial scales indicating, reasonable agreement despite a Reynolds number mismatch. Multiple calculations are performed confirming weak sensitivity of low-order statistics and void fraction on the Reynolds number. The presented results provide, for the first time, a comprehensive quantitative data for a wide range of phenomena in a turbulent breaking wave using DNS. These include mean velocity fields, Reynolds stresses, turbulence production and dissipation, velocity spectra and air entrainment data. In addition, we present the energy budget as a function of streamwise location by keeping track of various energy exchange processes in the wake of the jump. The kinetic energy is mostly transferred to pressure work, potential energy and dissipation while surface energy plays a less significant role. Our results indicate that the rate associated with various energy exchange processes peak at different streamwise locations, with exchange to pressure work flux peaking first, followed by potential energy flux and then dissipation. The energy exchange process spans a streamwise length of order 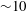${\sim}10$ jump heights. Furthermore, we report statistics associated with bubble transport downstream of the jump. The bubble formation is found to have a periodic nature. Meaning that the bubbles are generated in patches with a specific frequency associated with the roll-up frequency of the roller at the toe of the jump, with its footprint apparent in the velocity energy spectrum. Our study also provides the ensemble-averaged statistics of the flow which we present in this paper. These results are useful for the development and validation of reduced-order models such as dissipation models in wave dynamics simulations, Reynolds-averaged Navier–Stokes models and air entrainment models.

JFM classification

Multiphase and Particle-laden Flows: Gas/liquid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 797 , 25 June 2016 , pp. 60 - 94
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brattberg, T., Toombes, L. & Chanson, H. 1998 Developing air–water shear layers of two-dimensional water jets discharging into air. In ASME Fluids Engineering Division Summer Meeting, Washington, DC.Google Scholar
Carvalho, R., Lemos, C. & Ramos, C. 2008 Numerical computation of the flow in hydraulic jump stilling basins. J. Hydraul. Res. 46, 739–752.CrossRefGoogle Scholar
Chanson, H. 1995 Air entrainment in two-dimensional turbulent shear flows with partially developed inflow conditions. Intl J. Multiphase Flow 21, 1107–1121.CrossRefGoogle Scholar
Chanson, H. 1996 Air Bubble Entrainment in Free Surface Turbulent Flows. Academic Press.Google Scholar
Chanson, H. 2007a Bubbly flow structure in hydraulic jump. Eur. J. Mech. (B/Fluids) 26, 367–384.CrossRefGoogle Scholar
Chanson, H.2007b Dynamic similarity and scale effects affecting air bubble entrainment in hydraulic jumps. In 6th International Conference on Multiphase Flow. Techmische Universität Darmstadt.CrossRefGoogle Scholar
Chanson, H. 2009 Current knowledge in hydraulic jumps and related phenomena. A survey of experimental results. Eur. J. Mech. (B/Fluids) 28, 191–210.CrossRefGoogle Scholar
Chanson, H. & Brattberg, T. 2000 Experimental study of the air–water shear flow in a hydraulic jump. Intl J. Multiphase Flow 26, 583–607.CrossRefGoogle Scholar
Chippada, S., Ramaswamy, B. & Wheeler, M. 1994 Numerical simulation of hydraulic jump. Intl J. Numer. Meth. Engng 37, 1381–1397.CrossRefGoogle Scholar
Clay, P. 1940 The mechanism of emulsion formation in turbulent flow: theoretical part and dissuasion. Proc. R. Acad. Sci. 43, 979–990.Google Scholar
Deane, G. & Stokes, M. 2002 Scale dependence of bubble creation mechanisms in breaking waves. Nature 418, 839–844.CrossRefGoogle ScholarPubMed
Dimotakis, P. 1986 Two-dimensional shear-layer entrainment. AIAA J. 24, 1791–1796.CrossRefGoogle Scholar
Dong, R., Katz, J. & Huang, T. 1997 On the structure of bow waves on a ship model. J. Fluid Mech. 346, 77–115.CrossRefGoogle Scholar
Duncan, J. 2001 Spilling breakers. Annu. Rev. Fluid Mech. 33, 519–547.CrossRefGoogle Scholar
Duncan, J., Qiao, H., Philomin, V. & Wenz, A. 1999 Gentle spilling breakers: crest profile evolution. J. Fluid Mech. 379, 191–222.CrossRefGoogle Scholar
Fedkiw, R., Aslam, T., Merriman, B. & Osher, S. 1999 A non-oscillatory eulerian approach to interfaces in multi material flows (the ghost fluid method). J. Comput. Phys. 152, 457–492.CrossRefGoogle Scholar
Garrett, C., Li, M. & Farmer, D. 2000 The connection between bubble size spectrum and energy dissipation rates in the upper ocean. J. Phys. Oceanogr. 30, 2163–2171.2.0.CO;2>CrossRefGoogle Scholar
Gharangik, A. & Chaudhry, M. 1991 Numerical simulation of hydraulic jump. J. Hydraul. Engng ASCE 117, 1195–1211.CrossRefGoogle Scholar
Hinze, J. 1955 Fundamentals of the hydraulic mechanism of splitting in dispersion processes. AIChE J. 1, 289–295.CrossRefGoogle Scholar
Hornung, H., Willert, C. & Turner, S. 1995 The flow field downstream of a hydraulic jump. J. Fluid Mech. 287, 299–316.CrossRefGoogle Scholar
Kiger, K. & Duncan, J. 2012 Air-entrainment mechanisms in plunging jets and breaking waves. Annu. Rev. Fluid Mech. 44, 563–596.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fraction-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.CrossRefGoogle Scholar
King, C. 1995 Depth of disturbance of sand on sea beaches by waves. J. Sedim. Petrol. 21, 131–140.Google Scholar
Kolmogorov, N. 1949 On the drops breakup in the turbulent flow. Gidromekanika 66, 825–828.Google Scholar
Lakehal, D. & Liovic, P. 2011 Turbulence structure and interaction with steep breaking waves. J. Fluid Mech. 674, 522–577.CrossRefGoogle Scholar
Lamarre, E. & Melville, W. 1991 Air entrainment and dissipation in breaking waves. Nature 351, 469–472.CrossRefGoogle Scholar
Le-Chenadec, V. & Pitsch, H. 2013 A 3d unsplit forward/backward volume-of-fluid approach and coupling to the level set method. J. Comput. Phys. 233, 10–33.CrossRefGoogle Scholar
Leng, X. & Chanson, H. 2015 Turbulent advances of a breaking bore: preliminary physical experiments. Exp. Therm. Fluid Sci. 62, 70–77.CrossRefGoogle Scholar
Li, M. & Garrett, C. 1998 The relationship between oil droplet size and upper ocean turbulence. Mar. Pollut. Bull. 36, 961–970.CrossRefGoogle Scholar
Lin, C., Hsieh, S., Lin, I., Chang, K. & Raikar, R. 2012 Flow property and self-similarity in steady hydraulic jumps. Exp. Fluids 53, 1591–1616.CrossRefGoogle Scholar
Liu, M., Rajaratnam, N. & Zhu, D. 2004 Turbulence structure of hydraulic jumps of low Froude numbers. J. Hydraul. Engng ASCE 130, 511–520.CrossRefGoogle Scholar
Liu, X. & Duncan, J. 2003 The effects of surfactants on spilling breaking waves. Nature 421, 520–523.CrossRefGoogle ScholarPubMed
Liu, X. & Duncan, J. 2006 An experimental study of surfactant effects on spilling breakers. J. Fluid Mech. 567, 433–455.CrossRefGoogle Scholar
Long, D., Rajaratnam, N., Steffler, P. & Smy, P. 1991a Structure of flow in hydraulic jumps. J. Hydraul. Res. 29, 207–218.CrossRefGoogle Scholar
Long, D., Steffler, P. & Rajaratnam, N. 1991b A numerical study of submerged hydraulic jumps. J. Hydraul. Res. 29 (3), 293–308.CrossRefGoogle Scholar
Lubin, P., Glockner, S. & Chanson, H. 2009 Numerical simulation of air entrainment and turbulence in a hydraulic jump. Colloque SHF 109–114.Google Scholar
Lubin, P., Vincent, S., Abadie, S. & Caltagirone, J. P. 2006 Three-dimensional large eddy simulation of air entrainment under plunging breaking waves. Coast. Engng 53, 631–655.CrossRefGoogle Scholar
Ma, F., Hou, Y. & Prinos, P. 2001 Numerical calculation of submerged hydraulic jumps. J. Hydraul. Res. 39, 493–503.CrossRefGoogle Scholar
Ma, J., Oberai, A., Drew, D. & Lahey, R. Jr 2012 A two-way coupled polydispersed two-fluid model for the simulation of air entrainment beneath a plunging liquid jet. J. Fluids Engng 134, 101304.CrossRefGoogle Scholar
Ma, J., Oberai, A., Lahey, R. Jr & Drew, D. 2011 Modeling air entrainment and transport in a hydraulic jump using two-fluid RANS and DES turbulence models. Heat Mass Transfer 47, 911–919.CrossRefGoogle Scholar
Madsen, P. & Svendsen, I. 1983 Turbulent bores and hydraulic jumps. J. Fluid Mech. 129, 1–25.CrossRefGoogle Scholar
Misra, S., Kirby, J., Brocchini, M., Veron, F., Thomas, M. & Kambhamettu, C. 2008 The mean and turbulent flow structure of a weak hydraulic jump. Phys. Fluids 20, 035106.CrossRefGoogle Scholar
Mok, K. 2004 Relation of surface roller eddy formation and surface fluctuation in hydraulic jumps. J. Hydraul. Res. 4, 207–212.CrossRefGoogle Scholar
Moraga, F., Carrica, P., Drew, D. Jr & Lahey, R. 2008 A sub-grid air entrainment model for breaking bow waves and naval surface ships. Comput. Fluids 37, 281–298.CrossRefGoogle Scholar
Murzyn, F. & Chanson, H. 2008 Experimental assessment of scale effects affecting two-phase flow properties in hydraulic jumps. Exp. Fluids 45, 513–521.CrossRefGoogle Scholar
Murzyn, F. & Chanson, H. 2009a Free-surface fluctuations in hydraulic jumps: experimental observations. Exp. Therm. Fluid Sci. 33, 1055–1064.CrossRefGoogle Scholar
Murzyn, F. & Chanson, H. 2009b Two-Phase Gas-Liquid Flow Properties in the Hydraulic Jump: Review and Perspectives, chap. 9, Nova Science.Google Scholar
Murzyn, F., Mouaze, D. & Chaplin, J. 2005 Optical fibre probe measurements of bubbly flow in hydraulic jumps. Intl J. Multiphase Flow 31, 141–154.CrossRefGoogle Scholar
Murzyn, F., Mouaze, D. & Chaplin, J. 2007 Air–water interface dynamic and free surface features in hydraulic jumps. J. Hydraul. Res. 45, 679–685.CrossRefGoogle Scholar
Osher, S. & Sethian, J. 1988 Front propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 79, 12–49.CrossRefGoogle Scholar
Pauley, L., Moin, P. & Reynolds, W. 1990 The structure of two-dimensional separation. J. Fluid Mech. 220, 397–411.CrossRefGoogle Scholar
Qiao, H. & Duncan, J. 2001 Gentle spilling breakers: crest flow-field evolution. J. Fluid Mech. 439, 57–85.CrossRefGoogle Scholar
Resch, F. & Leutheusser, H. 1972 Reynolds stress measurements in hydraulic jumps. J. Hydraul. Res. 10, 409–430.CrossRefGoogle Scholar
Richard, G. & Gavrilyuk, S. 2013 The classical hydraulic jump in a model of shear shallow-water flows. J. Fluid Mech. 725, 492–521.CrossRefGoogle Scholar
van Rijn, L. 1993 Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas. Aqua.Google Scholar
Rodriguez-Rodriguez, J., Marugan-Cruz, C., Aliseda, A. & Lasheras, J. 2011 Dynamics of large turbulent structures in a steady breaker. Exp. Therm. Fluid Sci. 35, 301–310.CrossRefGoogle Scholar
Rouse, H., Siao, T. & Nagaratnam, S. 1959 Turbulence characteristics of the hydraulic jump. Trans. ASCE 124, 926–950.Google Scholar
Tahara, Y. & Stern, F. 1996 A large-domain approach for calculating ship boundary layers and wakes and wave fields for nonzero Froude number. J. Comput. Phys. 127, 398–411.CrossRefGoogle Scholar
Wang, H., Murzyn, F. & Chanson, H. 2014 Total pressure fluctuation and two-phae flow turbulence in hydraulic jumps. Exp. Fluids 55, 1847.CrossRefGoogle Scholar
Wilson, R., Carrica, P. & Stern, F. 2007 Simulation of ship breaking bow waves an induced vortices and scars. Intl J. Numer. Meth. Fluids 54, 419–451.CrossRefGoogle Scholar
Zhou, J. & Stansby, P. 1999 2D shallow water flow model for the hydraulic jump. Intl J. Numer. Meth. Fluids 29, 375–387.3.0.CO;2-3>CrossRefGoogle Scholar

Mortazavi et al. supplementary movie

Simulation of turbulent hydraulic jump at Fr=2.0, We=1820, and Re=11000. Shown is the air-water interface defined by VF=0.5.

Download Mortazavi et al. supplementary movie(Video)
Video 30.8 MB

Mortazavi et al. supplementary movie

Simulation of turbulent hydraulic jump at Fr=2.0, We=1820, and Re=11000. Shown is the air-water interface defined by VF=0.5.

Download Mortazavi et al. supplementary movie(Video)
Video 29.1 MB