Article contents
Direct numerical simulation of a turbulent core-annular flow with water-lubricated high viscosity oil in a vertical pipe
Published online by Cambridge University Press: 20 June 2018
Abstract
The characteristics of a turbulent core-annular flow with water-lubricated high viscosity oil in a vertical pipe are investigated using direct numerical simulation, in conjunction with a level-set method to track the phase interface between oil and water. At a given mean wall friction (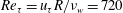 $Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}R/\unicode[STIX]{x1D708}_{w}=720$, where
$Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}R/\unicode[STIX]{x1D708}_{w}=720$, where 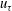 $u_{\unicode[STIX]{x1D70F}}$ is the friction velocity,
$u_{\unicode[STIX]{x1D70F}}$ is the friction velocity,  $R$ is the pipe radius and
$R$ is the pipe radius and 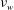 $\unicode[STIX]{x1D708}_{w}$ is the kinematic viscosity of water), the total volume flow rate of a core-annular flow is similar to that of a turbulent single-phase pipe flow of water, indicating that water lubrication is an effective tool to transport high viscosity oil in a pipe. The high viscosity oil flow in the core region is almost a plug flow due to its high viscosity, and the water flow in the annular region is turbulent except for the case of large oil volume fraction (e.g. 0.91 in the present study). With decreasing oil volume fraction, the mean velocity profile in the annulus becomes more like that of turbulent pipe flow, but the streamwise evolution of vortical structures is obstructed by the phase interface wave. In a reference frame moving with the core velocity, water is observed to be trapped inside the wave valley in the annulus, and only a small amount of water runs through the wave crest. The phase interface of the core-annular flow consists of different streamwise and azimuthal wavenumber components for different oil holdups. The azimuthal wavenumber spectra of the phase interface amplitude have largest power at the smallest wavenumber whose corresponding wavelength is the pipe circumference, while the streamwise wavenumber having the largest power decreases with decreasing oil volume fraction. The overall convection velocity of the phase interface is slightly lower than the core velocity. Finally, we suggest a predictive oil holdup model by defining the displacement thickness in the annulus and considering the boundary layer characteristics of water flow. This model predicts the variation of the oil holdup with the superficial velocity ratio very well.
$\unicode[STIX]{x1D708}_{w}$ is the kinematic viscosity of water), the total volume flow rate of a core-annular flow is similar to that of a turbulent single-phase pipe flow of water, indicating that water lubrication is an effective tool to transport high viscosity oil in a pipe. The high viscosity oil flow in the core region is almost a plug flow due to its high viscosity, and the water flow in the annular region is turbulent except for the case of large oil volume fraction (e.g. 0.91 in the present study). With decreasing oil volume fraction, the mean velocity profile in the annulus becomes more like that of turbulent pipe flow, but the streamwise evolution of vortical structures is obstructed by the phase interface wave. In a reference frame moving with the core velocity, water is observed to be trapped inside the wave valley in the annulus, and only a small amount of water runs through the wave crest. The phase interface of the core-annular flow consists of different streamwise and azimuthal wavenumber components for different oil holdups. The azimuthal wavenumber spectra of the phase interface amplitude have largest power at the smallest wavenumber whose corresponding wavelength is the pipe circumference, while the streamwise wavenumber having the largest power decreases with decreasing oil volume fraction. The overall convection velocity of the phase interface is slightly lower than the core velocity. Finally, we suggest a predictive oil holdup model by defining the displacement thickness in the annulus and considering the boundary layer characteristics of water flow. This model predicts the variation of the oil holdup with the superficial velocity ratio very well.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 20
- Cited by



