Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T23:14:32.122Z Has data issue: false hasContentIssue false
  • English
  • Français

A dipole solution for power-law gravity currents in porous formations

Published online by Cambridge University Press:  04 August 2015

S. Longo Open the ORCID record for S. Longo [Opens in a new window] ,
V. Di Federico  and
L. Chiapponi
S. Longo*
Affiliation:
Dipartimento di Ingegneria Civile, Ambiente Territorio e Architettura (DICATeA), Università di Parma, Parco Area delle Scienze, 181/A, 43124 Parma, Italy
V. Di Federico
Affiliation:
Dipartimento di Ingegneria Civile, Chimica, Ambientale e dei Materiali (DICAM), Università di Bologna, Viale Risorgimento, 2, 40136 Bologna, Italy
L. Chiapponi
Affiliation:
Dipartimento di Ingegneria Civile, Ambiente Territorio e Architettura (DICATeA), Università di Parma, Parco Area delle Scienze, 181/A, 43124 Parma, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A theoretical and experimental analysis of non-Newtonian gravity currents in porous media with variable properties is presented. A mound of a power-law fluid of flow behaviour index $n$ is released into a semi-infinite saturated porous medium above a horizontal bed, and can drain freely out of the formation at the origin. The porous medium permeability varies along the vertical as 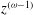$z^{({\it\omega}-1)}$, porosity varies along the vertical as 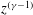$z^{({\it\gamma}-1)}$, $z$ being the vertical coordinate and 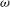${\it\omega}$ and 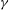${\it\gamma}$ constant numerical coefficients. A self-similar solution describing the space–time evolution of the resulting gravity current is derived for shear-thinning fluids with 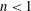$n<1$, generalizing earlier results for Newtonian fluids. The solution conserves a generalized dipole moment of the mound. The spreading of the current front is proportional to 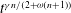$t^{{\it\gamma}n/(2+{\it\omega}(n+1))}$. Expressions for the time evolution of the outgoing flux at the origin and of the current volume are derived in closed form. The Hele-Shaw analogue is derived for flow of a power-law fluid in a porous medium with vertically variable properties. Results from laboratory experiments conducted in two Hele-Shaw cells confirm the constancy of the dipole moment, and compare well with the theoretical formulation.

JFM classification

Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Hele-Shaw flows Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , pp. 534 - 551
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aronsson, G. & Janfalk, U. 1992 On Hele-Shaw flow of power-law fluids. Eur. J. Appl. Maths 3, 343–366.CrossRefGoogle Scholar
Barenblatt, G. I. 1952 On some unsteady motions of fluids and gases in porous medium. Prikl. Mat. Mekh. 16 (1), 67–78.Google Scholar
Barenblatt, G. I. & Vazquez, J. L. 1998 A new free boundary problem for unsteady flows in porous media. Eur. J. Appl. Maths 9, 37–54.Google Scholar
Barenblatt, G. I. & Zel’dovich, Y. 1957 On dipole solutions in problems of non-stationary filtration of gas under polytropic regime. Prikl. Mat. Mekh. 21 (5), 718–720.Google Scholar
Bataller, R. C. 2008 On unsteady gravity flows of a power-law fluid through a porous medium. Appl. Maths Comput. 196, 356–362.CrossRefGoogle Scholar
Bear, J. 1972 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Burger, J. H., Haldenwang, R. & Alderman, N. J. 2015 Laminar and turbulent flow of non-newtonian fluids in open channels for different cross-sectional shapes. J. Hydraul. Engng 141 (4), 04014084.CrossRefGoogle Scholar
Ciriello, V. & Di Federico, V. 2012 Similarity solutions for flow of non-Newtonian fluids in porous media revisited under parameter uncertainty. Adv. Water Resour. 43, 38–51.Google Scholar
Cristopher, R. H. & Middleman, S. 1965 Power-law flow through a packed tube. Ind. Engng Chem. Fundam. 4, 422–427.CrossRefGoogle Scholar
Di Federico, V., Archetti, R. & Longo, S. 2012a Similarity solutions for spreading of a two-dimensional non-Newtonian gravity current. J. Non-Newtonian Fluid Mech. 177–178, 46–53.CrossRefGoogle Scholar
Di Federico, V., Archetti, R. & Longo, S. 2012b Spreading of axisymmetric non-Newtonian power-law gravity currents in porous media. J. Non-Newtonian Fluid Mech. 189–190, 31–39.Google Scholar
Di Federico, V., Longo, S., Chiapponi, L., Archetti, R. & Ciriello, V. 2014 Radial gravity currents in vertically graded porous media: theory and experiments for Newtonian and power-law fluids. Adv. Water Resour. 70, 65–76.CrossRefGoogle Scholar
Dullien, F. A. 1992 Porous Media: Fluid Transport and Pore Structure. Academic.Google Scholar
Hulshof, J. & Vazquez, J. L. 1993 The dipole solution for the porous medium equation in several space dimensions. Ann. Sci. Norm. Sup. Pisa Cl. Sci. (5) 20 (2), 193–217.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
Jiang, X.-W., Wang, X.-S. & Wan, L. 2010 Semi-empirical equations for the systematic decrease in permeability with depth in porous and fractured media. J. Hydrol. 18 (4), 839–850.Google Scholar
King, S. E.2000 Non-Newtonian gravity currents in Hele-Shaw cells. MSc thesis, University of Bristol.Google Scholar
King, S. E. & Woods, A. W. 2003 Dipole solutions for viscous gravity currents: theory and experiments. J. Fluid Mech. 483, 91–109.Google Scholar
Kondic, L., Palffy-Muhoray, P. & Shelley, M. J. 1996 Models of non-Newtonian Hele-Shaw flow. Phys. Rev. E 54 (5), 4536–4539.Google Scholar
Longo, S., Di Federico, V., Archetti, R., Chiapponi, L., Ciriello, V. & Ungarish, M. 2013a On the axisymmetric spreading of non-newtonian power-law gravity currents of time-dependent volume: an experimental and theoretical investigation focused on the inference of rheological parameters. J. Non-Newtonian Fluid Mech. 201 (0), 69–79.Google Scholar
Longo, S., Di Federico, V., Chiapponi, L. & Archetti, R. 2013b Experimental verification of power-law non-Newtonian axisymmetric porous gravity currents. J. Fluid Mech. 731, R2, 1–12.Google Scholar
Lyle, S., Huppert, H. E., Hallworth, M., Bickle, M. & Chadwick, A. 2005 Axisymmetric gravity currents in a porous medium. J. Fluid Mech. 543, 293–302.CrossRefGoogle Scholar
Mathunjwa, J. S. & Hogg, A. J. 2007 Freely draining gravity currents in porous media: dipole self-similar solutions with and without capillary retention. Eur. J. Appl. Maths. 18, 337–362.Google Scholar
Pascal, H. 1983 Nonsteady flow of non-Newtonian fluids through a porous medium. Intl J. Engng Sci. 21, 199–210.Google Scholar
Pascal, J. P. & Pascal, H. 1993 Similarity solutions to gravity flows of non-Newtonian fluids through porous media. Intl J. Non-Linear Mech. 28 (2), 157–167.Google Scholar
Phillips, O. M. 1991 Flow and Reactions in Porous Rocks. Cambridge University Press.Google Scholar
Shenoy, A. V. 1995 Non-Newtonian fluid heat transfer in porous media. Adv. Heat Transfer 24, 102–190.Google Scholar
Tosco, T., Papini, M., Viggi, C. & Sethi, R. 2014 Nanoscale zerovalent iron particles for groundwater remediation: a review. J. Clean Prod. 77, 10–21.Google Scholar
Ungarish, M. 2009 An Introduction to Gravity Currents and Intrusions. CRC Press.Google Scholar
Vossoughi, S. 1999 Flow of non-newtonian fluids in porous media. In Advances in the Flow and Rheology of Non-Newtonian Fluids, vol. 2, pp. 1183–1236. Elsevier Science Publishing Company.CrossRefGoogle Scholar
Wagner, B. 2005 An asymptotic approach to second-kind similarity solutions of the modified porous-medium equation. J. Engng Maths 53, 201–220.Google Scholar
Wu, Y.-S. & Pruess, K. 1996 Flow of non-Newtonian fluids in porous media. In Advances in Porous Media, vol. 3, pp. 87–184. Elsevier.Google Scholar
Yilmaz, N. A., Testik, F. Y. & Chowdury, M. R. 2014 Laminar bottom gravity currents: friction factor-Reynolds number relationship. J. Hydraul Res. 52 (4), 545–558.CrossRefGoogle Scholar
Zheng, Z., Soh, B., Huppert, H. E. & Stone, H. A. 2013 Fluid drainage from the edge of a porous reservoir. J. Fluid Mech. 718, 558–568.CrossRefGoogle Scholar