Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T03:19:48.071Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimensionality, secondary flows and helicity in low-Rm MHD vortices

Published online by Cambridge University Press:  14 August 2015

Nathaniel T. Baker ,
Alban Pothérat  and
Laurent Davoust
Nathaniel T. Baker*
Affiliation:
Coventry University, Applied Mathematics Research Center, Priory Street, Coventry CV1 5FB, UK Grenoble-INP/CNRS/University Grenoble-Alpes, SIMaP, Electromagnetic Processing of Materials (EPM) Laboratory, F-38000 Grenoble, France CNRS LNCMI, 38042 Grenoble, France
Alban Pothérat
Affiliation:
Coventry University, Applied Mathematics Research Center, Priory Street, Coventry CV1 5FB, UK
Laurent Davoust
Affiliation:
Grenoble-INP/CNRS/University Grenoble-Alpes, SIMaP, Electromagnetic Processing of Materials (EPM) Laboratory, F-38000 Grenoble, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we examine the dimensionality of a single electrically driven vortex bounded by two no-slip and perfectly insulating horizontal walls a distance 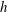$h$ apart. The study was performed in the weakly inertial limit by means of an asymptotic expansion, which is valid for any Hartmann number. We show that the dimensionality of the leading order can be fully described using the single parameter 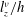$l_{z}^{{\it\nu}}/h$, where 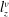$l_{z}^{{\it\nu}}$ represents the distance over which the Lorentz force is able to act before being balanced by viscous dissipation. The base flow happens to introduce inertial recirculations in the meridional plane at the first order, which are shown to follow two radically different mechanisms: inverse Ekman pumping driven by a vertical pressure gradient along the axis of the vortex, or direct Ekman pumping driven by a radial pressure gradient in the Hartmann boundary layers. We demonstrate that when the base flow is quasi-2D, the relative importance of direct and inverse pumping is solely determined by the aspect ratio ${\it\eta}/h$, where ${\it\eta}$ refers to the width of the vortex. Of the two mechanisms, only inverse pumping appears to act as a significant source of helicity.

JFM classification

Waves/Free-surface Flows: Channel flow MHD and Electrohydrodynamics: MHD and Electrohydrodynamics Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 779 , 25 September 2015 , pp. 325 - 350
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akkermans, R. A. D., Cieslik, A. R., Kamp, L. P. J., Trieling, R. R., Clercx, H. J. H. & Van Heijst, G. J. F. 2008 The three-dimensional structure of an electromagnetically generated dipolar vortex in a shallow fluid layer. Phys. Fluids 20, 116601.CrossRefGoogle Scholar
Clercx, H. J. H. & Van Heijst, G. 2009 Two-dimensional Navier–Stokes turbulence in bounded domains. Appl. Mech. Rev. 62, 1–25.CrossRefGoogle Scholar
Davidson, P. A. 2014 The dynamics and scaling laws of planetary dynamos driven by inertial waves. Geophys. J. Intl 198 (3), 1832–1847.CrossRefGoogle Scholar
Davoust, L., Achard, J.-L. & Drazek, L. 2015 Low-to-moderate Reynolds number swirling flow in an annular channel with a rotating end wall. Phys. Rev. E 91, 023019.CrossRefGoogle Scholar
Deusebio, E. & Lindborg, E. 2014 Helicity in the Ekman boundary layer. J. Fluid Mech. 755, 654–671.CrossRefGoogle Scholar
Ekman, V. W. 1905 On the influence of the Earth’s rotation on ocean currents. Ark. Mat. Astron. Fys. 2, 1–53.Google Scholar
Gilbert, A. D., Frisch, U. & Pouquet, A. 1988 Helicity is unnecessary for alpha effect dynamos, but it helps. Geophys. Astrophys. Fluid Dyn. 42 (1–2), 151–161.CrossRefGoogle Scholar
Kalis, Kh. E. & Kolesnikov, Yu. B. 1980 Numerical study of a single vortex of a viscous incompressible electrically conducting fluid in a homogeneous axial magnetic field. Magnetohydrodynamics 16, 155–158.Google Scholar
Klein, R. & Pothérat, A. 2010 Appearance of three-dimensionality in wall bounded MHD flows. Phys. Rev. Lett. 104 (3), 034502.CrossRefGoogle ScholarPubMed
Kornet, K. & Pothérat, A. 2015 A method for spectral DNS of low Rm channel flows based on the least dissipative modes. J. Comput. Phys. 298, 266–279.CrossRefGoogle Scholar
Lindborg, E. 1999 Can the atmospheric kinetic energy spectrum be explained by two-dimensional turbulence? J. Fluid Mech. 388, 259–288.CrossRefGoogle Scholar
Messadek, K. & Moreau, R. 2002 An experimental investigation of MHD quasi-two-dimensional turbulent shear flows. J. Fluid Mech. 456, 137–159.CrossRefGoogle Scholar
Pothérat, A. & Klein, R. 2014 Why, how and when MHD turbulence at low Rm becomes three-dimensional. J. Fluid Mech. 761, 168–205.CrossRefGoogle Scholar
Pothérat, A., Rubiconi, F., Charles, Y. & Dousset, V. 2013 Direct and inverse pumping in flows with homogeneous and non-homogeneous swirl. Eur. Phys. J. E 36 (8), 94.CrossRefGoogle ScholarPubMed
Pothérat, A., Sommeria, J. & Moreau, R. 2000 An effective two-dimensional model for MHD flows with transverse magnetic field. J. Fluid Mech. 424, 75–100.CrossRefGoogle Scholar
Pothérat, A., Sommeria, J. & Moreau, R. 2002 Effective boundary conditions for magnetohydrodynamic flows with thin Hartmann layers. Phys. Fluids 14 (1), 403–410.CrossRefGoogle Scholar
Roberts, P. H. 1967 Introduction to Magnetohydrodynamics. Longmans.Google Scholar
Satijn, M. P., Cense, A. W., Verzicco, H., Clercx, H. J. H. & van Heijst, G. J. F. 2001 Three-dimensional structure and decay properties of vortices in shallow fluid layers. Phys. Fluids 13 (7), 1932–1945.CrossRefGoogle Scholar
Shats, M., Byrne, D. & Xia, H. 2010 Turbulence decay rate as a measure of flow dimensionality. Phys. Rev. Lett. 105, 264501.CrossRefGoogle ScholarPubMed
Smith, D. M. 1991 Algorithm 693: a Fortran package for floating-point multiple-precision arithmetic. ACM Trans. Math. Softw. 17 (2), 273–283.CrossRefGoogle Scholar
Sommeria, J. 1988 Electrically driven vortices in a strong magnetic field. J. Fluid Mech. 189, 553–569.CrossRefGoogle Scholar
Sommeria, J. & Moreau, R. 1982 Why, how and when MHD turbulence becomes two-dimensional. J. Fluid Mech. 118, 507–518.CrossRefGoogle Scholar
Tabeling, P. 2002 Two-dimensional turbulence: a physicist approach. Phys. Rep. 362 (1), 1–62.CrossRefGoogle Scholar