Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-08T04:58:22.285Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential analysis of capillary breakup rheometry for Newtonian liquids

Published online by Cambridge University Press:  08 September 2016

Louise L. McCarroll ,
Michael J. Solomon  and
William W. Schultz
Louise L. McCarroll
Affiliation:
Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48109, USA
Michael J. Solomon
Affiliation:
Department of Chemical Engineering, University of Michigan, Ann Arbor, MI 48109, USA
William W. Schultz*
Affiliation:
Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48109, USA Department of Naval Architecture and Marine Engineering, University of Michigan, Ann Arbor, MI 48109, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a Newtonian, one-dimensional, differential analysis for capillary breakup rheometry (CBR) to determine the surface tension to viscosity ratio $\unicode[STIX]{x1D6FC}$. Our local differential analysis does not require specific assumptions for the axial force to preclude its measurement. Our analysis indicates that measuring gradients in filament curvature is necessary to accurately determine $\unicode[STIX]{x1D6FC}$ when axial force is not measured. CBR experiments were performed on five silicone oils (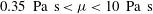$0.35~\text{Pa}~\text{s}<\unicode[STIX]{x1D707}<10~\text{ Pa}~\text{s}$), three sample volumes, and three strains to evaluate the operating range of the differential analysis and compare its performance to that of a standard integral method from literature. We investigate the role of filament asymmetry, caused mainly by gravity, on the performance of the differential method for the range of conditions studied. Experimental and analytical details for resolving gradients of curvature are also given.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Liquid bridges Non-Newtonian Flows: Rheology
Type
Papers
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , pp. 116 - 129
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anna, S. L. & Mckinley, G. H. 2001 Elasto-capillary thinning and breakup of model elastic liquids. J. Rheol. 45 (1), 115–138.CrossRefGoogle Scholar
Bazilevsky, A. V., Entov, V. M. & Rozhkov, A. N. 1990 Liquid filament microrheometer and some of its applications. In Third European Rheology Conference and Golden Jubilee Meeting of the British Society of Rheology, pp. 41–43. Springer.CrossRefGoogle Scholar
Bhat, P. P., Appathurai, S., Harris, M. T., Pasquali, M., Mckinley, G. H. & Basaran, O. A. 2010 Formation of beads-on-a-string structures during break-up of viscoelastic filaments. Nat. Phys. 6 (8), 625–631.CrossRefGoogle Scholar
Brenner, M. P., Lister, J. R. & Stone, H. A. 1996 Pinching threads, singularities and the number 0.0304.... Phys. Fluids 8 (11), 2827–2836.CrossRefGoogle Scholar
Canny, J. 1986 A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 8 (6), 679–698.CrossRefGoogle ScholarPubMed
Eggers, J. 1993 Universal pinching of 3D axisymmetric free-surface flow. Phys. Rev. Lett. 71 (21), 3458–3460.CrossRefGoogle ScholarPubMed
Eggers, J. 1997 Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 69 (3), 865–930.CrossRefGoogle Scholar
Kolte, M. I. & Szabo, P. 1999 Capillary thinning of polymeric filaments. J. Rheol. 43 (3), 609–625.CrossRefGoogle Scholar
Liang, R. & Mackley, M. 1994 Rheological characterization of the time and strain dependence for polyisobutylene solutions. J. Non-Newton. Fluid Mech. 52 (3), 387–405.CrossRefGoogle Scholar
Matta, J. & Tytus, R. 1990 Liquid stretching using a falling cylinder. J. Non-Newton. Fluid Mech. 35 (2–3), 215–229.CrossRefGoogle Scholar
Mckinley, G. H. & Tripathi, A. 2000 How to extract the Newtonian viscosity from capillary breakup measurements in a filament rheometer. J. Rheol. 44 (3), 653–670.CrossRefGoogle Scholar
Padday, J. F., Pitt, A. R. & Pashley, R. M. 1975 Menisci at a free liquid surface: surface tension from the maximum pull on a rod. J. Chem. Soc. Faraday Trans. 1 71, 1919–1931.CrossRefGoogle Scholar
Papageorgiou, D. T. 1995 On the breakup of viscous liquid threads. Phys. Fluids 7 (7), 1529–1544.CrossRefGoogle Scholar
Renardy, M. 1994 Some comments on the surface-tension driven break-up (or the lack of it) of viscoelastic jets. J. Non-Newton. Fluid Mech. 51 (1), 97–107.CrossRefGoogle Scholar
Schultz, W. W. & Davis, S. 1982 One-dimensional liquid fibers. J. Rheol. 26 (4), 331–345.CrossRefGoogle Scholar
Spiegelberg, S. H., Ables, D. C. & Mckinley, G. H. 1996 The role of end-effects on measurements of extensional viscosity in filament stretching rheometers. J. Non-Newton. Fluid Mech. 64 (2‐3), 229–267.CrossRefGoogle Scholar
Tirtaatmadja, V. & Sridhar, T. 1993 A filament stretching device for measurement of extensional viscosity. J. Rheol. 37 (6), 1081–1102.CrossRefGoogle Scholar