Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-26T12:12:50.312Z Has data issue: false hasContentIssue false
  • English
  • Français

Development of the trailing shear layer in a starting jet during pinch-off

Published online by Cambridge University Press:  30 April 2012

L. Gao  and
S. C. M. Yu
L. Gao*
Affiliation:
Division of Aerospace Engineering, School of Mechanical and Aerospace Engineering, Nanyang Technological University, Singapore 639798, Singapore
S. C. M. Yu
Affiliation:
Division of Aerospace Engineering, School of Mechanical and Aerospace Engineering, Nanyang Technological University, Singapore 639798, Singapore
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

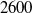Experiments on a circular starting jet generated by a piston–cylinder arrangement, over a range of Reynolds number from to 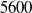, are conducted so as to investigate the development of the trailing shear layer during the leading vortex ring formation, as well as the corresponding effects on the pinch-off process. Results obtained by digital particle image velocimetry (DPIV) show that secondary vortices start to develop in the trailing jet only after the critical time scale, the ‘formation number’, is achieved. The subsequent growth of the secondary vortices reduces the vorticity flux being fed into the leading vortex ring and, as a consequence, constrains the growth of leading vortex ring with larger circulation. Evolution of perturbation waves into secondary vortices is found to associate with growth and translation of the leading vortex ring during the formation process. A dimensionless parameter ‘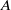’, defined as 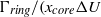), is therefore proposed to characterize the effect of the leading vortex ring on suppressing the nonlinear development of instability in the trailing shear layer, i.e. the initial roll-up of the secondary vortices. In a starting jet, 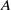follows a decreasing trend with the formation time 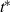. A critical value 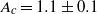is identified experimentally, which physically coincides with the initiation of the first secondary vortex roll-up and, therefore, indicates the onset of pinch-off process.

JFM classification

Wakes/Jets: Shear layers Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 700 , 10 June 2012 , pp. 382 - 405
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adrian, R. J. & Westerweel, J. 2010 Particle Image Velocimetry. Cambridge University Press.Google Scholar
2. Allen, J. J. & Naitoh, T. 2005 Experimental study of the production of vortex rings using a variable diameter orifice. Phys. Fluids 17, 061701.CrossRefGoogle Scholar
3. Benjamin, T. 1976 The alliance of practical and analytical insights into the nonlinear problems of fluid mechanics. Appl. Methods Funct. Anal. Probl. Mech. 503, 8–29.Google Scholar
4. Cohen, J. & Wygnanski, I. 1987 The evolution of instabilities in the axisymmetric jet. Part 1. The linear growth of disturbances near the nozzle. J. Fluid Mech. 176, 191–219.CrossRefGoogle Scholar
5. Dabiri, J. O. & Gharib, M. 2004 Delay of vortex ring pinchoff by an imposed bulk counterflow. Phys. Fluids 16, L28.CrossRefGoogle Scholar
6. Dabiri, J. O. & Gharib, M. 2005 Starting flow through nozzles with temporally variable exit diameter. J. Fluid Mech. 538, 111–136.CrossRefGoogle Scholar
7. Didden, N. 1979 On the formation of vortex rings: rolling-up and production of circulation. J. Appl. Math. Phys. (Z. Angew. Math. Phys.) 30 (1), 101–116.Google Scholar
8. Dring, R. P. 1982 Sizing criteria for laser anemometry particles. Trans. ASME: J. Fluids Engng 104 (1), 15–17.Google Scholar
9. Gao, L. & Yu, S. C. M. 2010 A model for the pinch-off process of the leading vortex ring in a starting jet. J. Fluid Mech. 656, 205–222.CrossRefGoogle Scholar
10. Gao, L., Yu, S. C. M., Ai, J. J. & Law, A. W. K. 2008 Circulation and energy of the leading vortex ring in a gravity-driven starting jet. Phys. Fluids 20, 093604.CrossRefGoogle Scholar
11. Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
12. Hjelmfelt, A. T. & Mockros, L. F. 1966 Motion of discrete particles in a turbulent fluid. Appl. Sci. Res. 16 (1), 149–161.CrossRefGoogle Scholar
13. Kelvin, L. 1880 Vortex statics. Phil. Mag. 10, 97–109.Google Scholar
14. Krueger, P. S., Dabiri, J. O. & Gharib, M. 2006 The formation number of vortex rings formed in uniform background co-flow. J. Fluid Mech. 556, 147–166.Google Scholar
15. Krueger, P. S. & Gharib, M. 2003 The significance of vortex ring formation to the impulse and thrust of a starting jet. Phys. Fluids 15, 1271.CrossRefGoogle Scholar
16. Lim, T. T. 1997 A note on the leapfrogging between two coaxial vortex rings at low Reynolds numbers. Phys. Fluids 9, 239.CrossRefGoogle Scholar
17. Maxworthy, T. 1972 The structure and stability of vortex rings. J. Fluid Mech. 51 (01), 15–32.CrossRefGoogle Scholar
18. Mei, R. 1996 Velocity fidelity of flow tracer particles. Exp. Fluids 22 (1), 1–13.CrossRefGoogle Scholar
19. Michalke, A. 1971 Instability of a compressible circular free jet with consideration of the influence of the jet boundary layer thickness. Z. Flugwissenschaften (West Germany) 19 (8), 319–328.Google Scholar
20. Michalke, A. & Hermann, G. 1982 On the inviscid instability of a circular jet with external flow. J. Fluid Mech. 114, 343–359.CrossRefGoogle Scholar
21. Mohseni, K. & Gharib, M. 1998 A model for universal time scale of vortex ring formation. Phys. Fluids 10, 2436.CrossRefGoogle Scholar
22. Mohseni, K., Ran, H. & Colonius, T. 2001 Numerical experiments on vortex ring formation. J. Fluid Mech. 430, 267–282.CrossRefGoogle Scholar
23. Morris, P. J. 1976 The spatial viscous instability of axisymmetric jets. J. Fluid Mech. 77 (03), 511–529.CrossRefGoogle Scholar
24. O’Farrell, C. & Dabiri, J. O. 2010 A Lagrangian approach to identifying vortex pinch-off. Chaos 20, 017513.Google ScholarPubMed
25. Pawlak, G., Marugan Cruz, C., Martínez Bazán, C. & García Hrdy, P. 2007 Experimental characterization of starting jet dynamics. Fluid Dyn. Res. 39 (11–12), 711–730.CrossRefGoogle Scholar
26. Riley, N. & Stevens, D. P. 1993 A note on leapfrogging vortex rings. Fluid Dyn. Res. 11 (5), 235–244.CrossRefGoogle Scholar
27. Rosenfeld, M., Rambod, E. & Gharib, M. 1998 Circulation and formation number of laminar vortex rings. J. Fluid Mech. 376, 297–318.CrossRefGoogle Scholar
28. Saffman, P. G. 1965 The lift on a small sphere in a shear flow. J. Fluid Mech. 22, 385–400.CrossRefGoogle Scholar
29. Saffman, P. G. 1968 Corrigendum to the lift on a small particle in a slow shear flow. J. Fluid Mech. 31, 624.Google Scholar
30. Saffman, P. G. 1995 Vortex Dynamics. Cambridge University Press.Google Scholar
31. Shusser, M. & Gharib, M. 2000 Energy and velocity of a forming vortex ring. Phys. Fluids 12, 618.CrossRefGoogle Scholar
32. Shusser, M., Gharib, M., Rosenfeld, M. & Mohseni, K. 2002 On the effect of pipe boundary layer growth on the formation of a laminar vortex ring generated by a piston/cylinder arrangement. Theor. Comput. Fluid Dyn. 15 (5), 303–316.CrossRefGoogle Scholar
33. Todde, V., Spazzini, P. G. & Sandberg, M. 2009 Experimental analysis of low-Reynolds number free jets. Exp. Fluids 47 (2), 279–294.CrossRefGoogle Scholar
34. Willert, C. E. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10 (4), 181–193.CrossRefGoogle Scholar
35. Zhao, W., Frankel, S. H. & Mongeau, L. G. 2000 Effects of trailing jet instability on vortex ring formation. Phys. Fluids 12, 589.CrossRefGoogle Scholar