Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T22:27:49.743Z Has data issue: false hasContentIssue false
  • English
  • Français

Development of gravity currents on slopes under different interfacial instability conditions

Published online by Cambridge University Press:  07 October 2019

Antoine Martin ,
M. Eletta Negretti Open the ORCID record for M. Eletta Negretti [Opens in a new window]  and
E. J. Hopfinger
Antoine Martin
Affiliation:
LEGI, UGA/CNRS, UMR 5519, 38000 Grenoble, France
M. Eletta Negretti*
Affiliation:
LEGI, UGA/CNRS, UMR 5519, 38000 Grenoble, France
E. J. Hopfinger
Affiliation:
LEGI, UGA/CNRS, UMR 5519, 38000 Grenoble, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present experimental results on the development of gravity currents moving onto sloping boundaries with slope angles 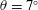$\unicode[STIX]{x1D703}=7^{\circ }$, 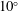$10^{\circ }$ and 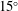$15^{\circ }$. Different regimes of flow development are observed depending on the slope angle and on the initial velocity and density profiles, characterized by the Richardson number 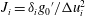$J_{i}=\unicode[STIX]{x1D6FF}_{i}{g_{0}}^{\prime }/\unicode[STIX]{x0394}u_{i}^{2}$, where 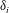$\unicode[STIX]{x1D6FF}_{i}$, 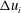$\unicode[STIX]{x0394}u_{i}$ and 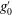$g_{0}^{\prime }$ are, respectively, the velocity interface thickness, the maximum velocity difference and reduced gravity at the beginning of the slope. For 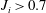$J_{i}>0.7$ and the larger slope angle, the flow strongly accelerates, reaches a maximum at the beginning of the Kelvin–Helmholtz instability, then decelerates and re-accelerates again. For 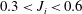$0.3<J_{i}<0.6$, instability occurs earlier and velocity oscillations are less. When 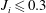$J_{i}\leqslant 0.3$ the increase in velocity is smooth. The magnitude of velocity oscillation depends on the combined effect of 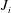$J_{i}$ and slope angle, expressed by an overall acceleration parameter 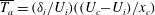$\overline{T_{a}}=(\unicode[STIX]{x1D6FF}_{i}/U_{i})((U_{c}-U_{i})/x_{c})$, which, to first order, is given by 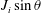$J_{i}\sin \unicode[STIX]{x1D703}$, where 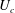$U_{c}$ and 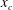$x_{c}$ are, respectively, the velocity and position at instability onset. The velocity increases smoothly up to an equilibrium state when 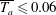$\overline{T_{a}}\leqslant 0.06$ and exhibits an irregular behaviour at larger values of 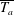$\overline{T_{a}}$. The critical Richardson number 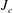$J_{c}$ decreases with increasing 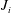$J_{i}$ (increasing 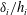$\unicode[STIX]{x1D6FF}_{i}/h_{i}$) which is due to wall effects and 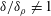$\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70C}}\neq 1$. After the beginning of Kelvin–Helmholtz instability, entrainment rates are close to those of a mixing layer, decreasing to values of a gravity current after the mixing layer reaches the boundary. It is shown here that the interfacial instability during current development affects the bottom shear stress which can reach values of 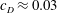$c_{D}\approx 0.03$ regardless of initial conditions. By solving numerically the depth integrated governing equations, the gravity flow velocity, depth and buoyant acceleration in the flow direction can be well predicted for all the performed experiments over the full measurement domain. The numerical results for the experiments with 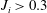$J_{i}>0.3$ predict that the current requires a distance of at least 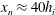$x_{n}\approx 40h_{i}$ to reach a normal state of constant velocity, which is much larger than the distance 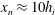$x_{n}\approx 10h_{i}$ required in the case of a current with 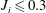$J_{i}\leqslant 0.3$ that is commonly assumed for downslope currents.

JFM classification

Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 180 - 208
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altinakar, M. S., Graf, W. H. & Hopfinger, E. J. 1990 Weakly depositing turbidity current on small slopes. J. Hydraul. Res. 28/1, 22–80.Google Scholar
Baines, P. G. & Condie, S. 1998 Observations and modelling of antartic downslope flows: a review. Ocean, Ice, and Atmosphere: Interactions at the Antarctic Continental Margin Antarctic Research Series 75, 29–49.Google Scholar
Britter, R. E. & Linden, P. F. 1980 The motion of the front of a gravity current travelling down an incline. J. Fluid Mech. 99 (3), 531–543.Google Scholar
Cenedese, C. & Adduce, C. 2010 A new parameterization for entrainment in overflows. J. Phys. Oceanogr. 40 (8), 1835–1850.Google Scholar
Cenedese, C., Whitehead, J. A., Ascarelli, T. A. & Ohiwa, M. 2004 A dense current flowing down a sloping bottom in a rotating fluid. J. Phys. Oceanogr. 34 (1), 188–203.Google Scholar
Cossu, R. & Wells, M. G. 2012 A comparison of the shear stress distribution in the bottom boundary layer of experimental density and turbidity currents. Eur. J. Mech. (B/Fluids) 32, 70–79.Google Scholar
Dallimore, C. J., Imberger, J. & Ishikawa, T. 2001 Entrainment and turbulence in saline underflow in lake ogawara. J. Hydraul. Engng 127 (11), 937–948.Google Scholar
Danabasoglu, G., Large, W. G. & Briegleb, B. P. 2010 Climate impacts of parameterized nordic sea overflows. J. Geophys. Res. 115, C11005.Google Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6 (3), 423–448.Google Scholar
Garcia, M. & Parker, G. 1993 Experiments on the entrainment of sediment into suspension by a dense bottom current. J. Geophys. Res. 98 (C3), 4793–4807.Google Scholar
George, W. K., Abrahamsson, H., Eriksson, J., Karlsson, R. I., Löfdahl, L. & Wosnik, M. 2000 A similarity theory for the turbulent plane wall jet without external stream. J. Fluid Mech. 425, 367–411.Google Scholar
Haigh, S. & Lawrence, G. A. 1999 Symmetric and non-symmetric holmboe instabilities in an inviscid flow. Phys. Fluids 6, 1459–1468.Google Scholar
Hazel, P. 1972 Numerical studies of the stability of inviscid stratified flows. J. Fluid Mech. 51, 39–61.Google Scholar
Hogg, A. M. & Ivey, G. N. 2003 The Kelvin–Helmholtz to holmboe instability transition in stratified exchange flows. J. Fluid Mech. 477, 339–362.Google Scholar
Koop, C. G. & Browand, F. K. 1979 Instability and turbulence in a stratified fluid with shear. J. Fluid Mech. 93 (1), 135–159.Google Scholar
Kostaschuk, R., Nasr-Azadani, M. M., Meiburg, E., Wei, T., Chen, Z., Negretti, M. E., Best, J., Peakall, J. & Parsons, D. R. 2018 On the causes of pulsing in continuous turbidity currents. J. Geophys. Res. 123 (11), 2827–2843.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2013 Experimental study of entrainment and interface dynamics in a gravity current. Exp. Fluids 54 (5), 1530.Google Scholar
Morton, B. R. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234 (1196), 1–23.Google Scholar
Negretti, M. E., Socolofsky, S. A. & Jirka, G. H. 2008 Linear stability analysis of inclined two-layers stratified flows. Phys. Fluids 20, 094104.Google Scholar
Negretti, M. E., Flòr, J.-B. & Hopfinger, E. J. 2017 Development of gravity currents on rapidly changing slopes. J. Fluid Mech. 833, 70–97.Google Scholar
Odier, P., Chen, J. & Ecke, R. E. 2014 Entrainment and mixing in a laboratory model of oceanic overflow. J. Fluid Mech. 746, 498–535.Google Scholar
Pawlak, G. & Armi, L. 2000 Mixing and entrainment in developing stratified currents. J. Fluid Mech. 424, 45–73.Google Scholar
Pokrajac, D., Venuleo, S. & Franca, M. J. 2017 Depth-averaged momentum equation for gravity currents with varying density: coefficient in pressure term. J. Hydraul Res. 1–7.Google Scholar
van Reeuwijk, M., Holzner, M. & Caulfield, C. P. 2019 Mixing and entrainment are suppressed in inclined gravity currents. J. Fluid Mech. 873, 786–815.Google Scholar
Sequeiros, O. E., Spinewine, B., Beaubouef, R. T., Sun, T., Garcia, M. H. & Parker, G. 2010 Bedload transport and bed resistance associated with density and turbidity currents. Sedimentology 57 (6), 1463–1490.Google Scholar
Sherman, F. S., Imberger, J. & Corcos, G. M. 1978 Turbulence and mixing in stably stratified waters. Annu. Rev. Fluid Mech. 10 (1), 267–288.Google Scholar
Simpson, J. E. & Britter, R. E. 1979 The dynamics of the head of a gravity current advancing over a horizontal surface. J. Fluid Mech. 94, 477–495.Google Scholar
Simpson, J. S. 1982 Gravity currents in the laboratory, atmosphere and ocean. Annu. Rev. Fluid Mech. 14, 213–234.Google Scholar
Strang, E. J. & Fernando, H. J. S. 2001 Vertical mixing and transports through a stratified shear layer. J. Phys. Oceanogr. 31(8), 2026–2048.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids, p. 405. Cambridge University Press.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Ungarish, M. 2011 Two-layer shallow-water dam-break solutions for non-Boussinesq gravity currents in a wide range of fractional depth. J. Fluid Mech. 675, 27–59.Google Scholar
Van Haren, H., Gostiaux, L., Morozov, E. & Tarakanov, R. 2014 Extremely long Kelvin–Helmholtz billow trains in the romanche fracture zone. Geophys. Res. Lett. 41 (23), 8445–8451.Google Scholar
Wirth, A. 2011 Estimation of friction parameters in gravity currents by data assimilation in a model hierarchy. Ocean Sci. 7 (2), 245–255.Google Scholar
Zhu, D. Z. & Lawrence, G. A. 2001 Holmboe’s instability in exchange flows. J. Fluid Mech. 429, 391–409.Google Scholar
Zordan, J., Juez, C., Schleiss, A. J. & Franca, M. J. 2018 Entrainment, transport and deposition of sediment by saline gravity currents. Adv. Water Resour. 115, 17–32.Google Scholar
Zordan, J., Schleiss, A. & Franca, M. J. 2019 Potential erosion capacity of gravity currents created by changing initial conditions. Earth Surf. Dyn. 7 (ARTICLE), 377–391.Google Scholar