Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T07:13:55.740Z Has data issue: false hasContentIssue false
  • English
  • Français

A detailed analysis of a dynamo mechanism in a rapidly rotating spherical shell

Published online by Cambridge University Press:  30 April 2012

F. Takahashi  and
H. Shimizu
F. Takahashi*
Affiliation:
Department of Earth and Planetary Sciences, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8551, Japan
H. Shimizu
Affiliation:
Earthquake Research Institute, University of Tokyo, 1-1-1 Yayoi, Bunkyo-ku, Tokyo 113-0032, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

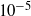Mechanisms of magnetic field intensification by flows of an electrically conducting fluid in a rapidly rotating spherical shell are investigated using a numerical dynamo model with an Ekman number of . A strong dipolar solution with a magnetic energy 55 times larger than the kinetic energy of thermal convection is obtained. In a regime of small viscosity and inertia with the strong magnetic field, the convection structure consists of a few large-scale retrograde flows in the azimuthal direction and localized thin sheet-like plumes. A detailed term-by-term analysis of the magnetic field amplification processes shows that the magnetic field is amplified through stretching of magnetic lines, which occurs typically through four types of flow: the retrograde azimuthal flow near the outer boundary, the downwelling flow of the sheet plume, the prograde azimuthal flow near the rim of the tangent cylinder, and the cylindrical-radially alternating flows of the plume cluster. The current loop structure emerges as a result of stretching the magnetic lines along the magnetic field by the flow acceleration. The most remarkable effects of the generated magnetic field on the flow come from the strong azimuthal (toroidal) magnetic field. Similarities of the present model in the convection and magnetic field structures to previous studies at larger and even smaller Ekman numbers suggest universality of the dynamo mechanism in rotating spherical dynamos.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory Geophysical and Geological Flows: Geodynamo Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 701 , 25 June 2012 , pp. 228 - 250
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Aubert, J., Aurnou, J. & Wicht, J. 2008 The magnetic structure of convection-driven numerical dynamos. Geophys. J. Intl 172, 945–956.CrossRefGoogle Scholar
2. Buffett, B. 2010 Tidal dissipation and the strength of the Earth’s internal magnetic field. Nature 468, 952–955.CrossRefGoogle ScholarPubMed
3. Bullard, E. C. & Gellman, H. 1954 Homogeneous dynamos and terrestrial magnetism. Phil. Trans. R. Soc. Lond. A 247, 213–278.Google Scholar
4. Busse, F. H. 1970 Thermal instabilities in rapidly rotating system. J. Fluid Mech. 44, 441–460.CrossRefGoogle Scholar
5. Cardin, P. & Olson, P. 1995 The influence of toroidal magnetic field on thermal convection in the core. Earth Planet. Sci. Lett. 132, 167–181.CrossRefGoogle Scholar
6. Christensen, U. R. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and applications planetary magnetic fields. Geophys. J. Intl 166, 97–114.CrossRefGoogle Scholar
7. Christensen, U. R., Olson, P. & Glatzmaier, G. A. 1998 A dynamo model interpretation of geomagnetic field structures. Geophys. Res. Lett. 25, 1565–1568.CrossRefGoogle Scholar
8. Christensen, U. R. & Wicht, J. 2007 Numerical dynamo simulations. In Treatise on Geophysics (ed. Olson, P. ), Core Dynamics , vol. 8. pp. 245–282. Elsevier.CrossRefGoogle Scholar
9. Elsasser, W. M. 1946 Induction effects in terrestrial magnetism I, theory. Phys. Rev. 69, 106–116.CrossRefGoogle Scholar
10. Gillet, N., Jault, D., Canet, E. & Fournier, A. 2010 Fast torsional waves and strong magnetic field within the Earth’s core. Nature 465, 74–77.CrossRefGoogle ScholarPubMed
11. Hori, K., Wicht, J. & Christensen, U. R. 2010 The effect of thermal boundary conditions on dynamos driven by internal heating. Phys. Earth Planet. Inter. 182, 85–97.CrossRefGoogle Scholar
12. Ishihara, N. & Kida, S. 2002 Dynamo mechanism in a rotating spherical shell: competition between magnetic field and convection vortices. J. Fluid Mech. 465, 1–32.CrossRefGoogle Scholar
13. Jackson, A. 2003 Intense equatorial flux spots on the surface of the Earth’s core. Nature 424, 760–763.CrossRefGoogle ScholarPubMed
14. Kageyama, A., Miyagoshi, T. & Sato, T. 2008 Formation of current coils in geodynamo simulations. Nature 454, 1106–1109.CrossRefGoogle ScholarPubMed
15. Kageyama, A. & Sato, T. 1997 Generation mechanism of a dipole field by a magnetohydrodynamic dynamo. Phys. Rev. E 55, 4617–4626.CrossRefGoogle Scholar
16. Kaiser, R. 1995 Towards a poloidal magnetic field theorem. Geophys. Astrophys. Fluid Dyn. 80, 129–144.CrossRefGoogle Scholar
17. Kitauchi, H. & Kida, S. 1998 Intensification of magnetic field by concentration-and-stretch of magnetic flux lines. Phys. Fluids 10, 457–468.CrossRefGoogle Scholar
18. Kono, M. & Roberts, P. H. 2002 Recent geodynamo simulations and observations of the geomagnetic field. Rev. Geophys. 40, 1013.CrossRefGoogle Scholar
19. Miyagoshi, T., Kageyama, A. & Sato, T. 2010 Zonal flow formation in the Earth’s core. Nature 463, 793–796.CrossRefGoogle ScholarPubMed
20. Miyagoshi, T., Kageyama, A. & Sato, T. 2011 Formation of sheet plumes, current coils, and helical magnetic fields in a spherical magnetohydrodynamic dynamo. Phys. Plasmas 18, 072901.CrossRefGoogle Scholar
21. Olson, P., Christensen, U. R. & Glatzmaier, G. A. 1999 Numerical modelling of the geodynamo: mechanisms of field generation and equilibration. J. Geophys. Res. 104, 10383–10404.CrossRefGoogle Scholar
22. Olson, P. & Glatzmaier, G. A. 1995 Magnetoconvection in a rotating spherical shell: structure of flow in the outer core. Phys. Earth Planet. Inter. 92, 109–118.CrossRefGoogle Scholar
23. Proctor, M. R. E. 2004 An extension of the toroidal theorem. Geophys. Astrophys. Fluid Dyn. 98, 235–240.CrossRefGoogle Scholar
24. Roberts, P. H. 1968 On the thermal instability of a rotating-fluid sphere containing heat sources. Phil. Trans. R. Soc. Lond. A 263, 93–117.Google Scholar
25. Sakuraba, A. 2002 Linear magnetoconvection in rotating fluid spheres permeated by a uniform axial magnetic field. Geophys. Astrophys. Fluid Dyn. 96, 291–318.CrossRefGoogle Scholar
26. Sakuraba, A. 2007 A jet-like structure revealed by a numerical simulation of rotating spherical-shell magnetoconvection. J. Fluid Mech. 573, 89–104.CrossRefGoogle Scholar
27. Sakuraba, A. & Kono, M. 1999 Effect of the inner core on the numerical solution of the magnetohydrodynamic dynamo. Phys. Earth Planet. Inter. 111, 105–121.CrossRefGoogle Scholar
28. Sakuraba, A. & Kono, M. 2000 Effect of a uniform magnetic field on nonlinear magnetoconvection in a rotating fluid spherical shell. Geophys. Astrophys. Fluid Dyn. 92, 255–287.CrossRefGoogle Scholar
29. Sakuraba, A. & Roberts, P. H. 2009 Generation of a strong magnetic field using uniform heat flux at the surface of the core. Nature Geosci. 2, 802–805.CrossRefGoogle Scholar
30. Sakuraba, A. & Roberts, P. H. 2011 On thermal driving of the geodynamo. In The Earth’s Magnetic Interior (ed. Petrovský, E., Herrero-Bervera, E., Harinarayana, T. & Ivers, D. ), pp. 117–129. Springer.CrossRefGoogle Scholar
31. Takahashi, F. 2012 Implementation of a high-order combined compact difference scheme in problems of thermally driven convection and dynamo in rotating spherical shells. Geophys. Astrophys. Fluid Dyn., doi:10.1080/03091929.2011.565337.CrossRefGoogle Scholar
32. Takahashi, F. & Matsushima, M. 2005 Dynamo action in a rotating spherical shell at high Rayleigh numbers. Phys. Fluids 17, 076601.CrossRefGoogle Scholar
33. Takahashi, F., Matsushima, M. & Honkura, Y. 2005 Simulations of a quasi-taylor state geomagnetic field including polarity reversals on the Earth simulator. Science 309, 459–461.CrossRefGoogle ScholarPubMed
34. Takahashi, F., Matsushima, M. & Honkura, Y. 2008 Scale variability in convection-driven MHD dynamos at low Ekman number. Phys. Earth Planet. Inter. 167, 168–178.CrossRefGoogle Scholar
35. de Wijs, G. A., Kresse, G., Vocadlo, L., Dobson, D., Alfe, D., Gillan, M. J. & Price, G. D. 1998 The viscosity of liquid iron at the physical conditions of the Earth’s core. Nature 392, 805–807.CrossRefGoogle Scholar