Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T02:12:51.555Z Has data issue: false hasContentIssue false
  • English
  • Français

Detached shear-layer instability and entrainment in the wake of a flat plate with turbulent separating boundary layers

Published online by Cambridge University Press:  03 June 2015

Man Mohan Rai
Man Mohan Rai*
Affiliation:
NASA Ames Research Center, Moffett Field, CA 94035, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The near and very near wake of a flat plate with a circular trailing edge, with vigorous vortex shedding, is investigated with data from direct numerical simulations (DNS). Computations were performed for four different combinations of the Reynolds numbers based on plate thickness (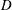$D$) and momentum thickness near the trailing edge (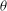${\it\theta}$). Unlike the case of the cylinder, these Reynolds numbers are independent parameters for the flat plate. The objectives of the study are twofold, to investigate the entrainment process when the separating boundary layers are turbulent and to better understand the instability of the detached shear layers (DSLs). A visualization of the entrainment process, the effect of changing the ratio 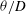${\it\theta}/D$ on entrainment and wake-velocity statistics, and a way of understanding entrainment in a phase-averaged sense via distributions of the turbulent transport rate are provided here. The discussion on shear-layer instability focuses on the role of log-layer eddies in the destabilization process, the effect of high-speed streaks in the turbulent boundary layer in the vicinity of the trailing edge on shear-layer vortex generation rates, and a relationship between the prevalence of shear-layer vortex generation and shedding phase that is a result of an interaction between the shedding process and the shear-layer instability mechanism. A power-law relationship between the ratio of shear-layer and shedding frequencies and the Reynolds numbers mentioned above is obtained. A discussion of the relative magnitudes of the exponents is provided. A second power-law relationship between shed-vortex strength and these two Reynolds numbers is also proposed.

JFM classification

Turbulent Flows: Shear layer turbulence Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 774 , 10 July 2015 , pp. 5 - 36
Check for updates
Copyright
© Cambridge University Press 2015. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bevilaqua, P. M. & Lykoudis, P. S. 1971 Mechanism of entrainment in turbulent wakes. AIAA J. 9, 1657–1659.Google Scholar
Bloor, M. S. 1964 The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 19, 290–304.Google Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.Google Scholar
Chevray, R. & Kovaznay, L. S. G. 1969 Turbulence measurements in the wake of a thin flat plate. AIAA J. 7, 1641–1643.Google Scholar
Dong, S., Karniadakis, G. E., Ekmekci, A. & Rockwell, D. 2006 A combined direct numerical simulation–particle velocimetry study of the turbulent near wake. J. Fluid Mech. 569, 185–207.Google Scholar
Gallardo, J. P., Andersson, H. I. & Pettersen, B. 2014 Turbulent wake behind a curved circular cylinder. J. Fluid Mech. 742, 192–229.CrossRefGoogle Scholar
Kim, J. & Choi, H.2001. Instability of the shear layer separating from a circular cylinder. In Proceedings of the Third AFOSR International Conference on DNS/LES, Arlington, TX, pp. 727–734.Google Scholar
Kopp, G. A., Giralt, F. & Keffer, J. F. 2002 Entrainment vortices and interfacial intermittent turbulent bulges in a plane turbulent wake. J. Fluid Mech. 469, 49–70.Google Scholar
Papailou, D. D. & Lykoudis, P. S. 1974 Turbulent vortex streets and the entrainment mechanism of the turbulent wake. J. Fluid Mech. 62, 11–31.Google Scholar
Prasad, A. & Williamson, C. H. K. 1997 The instability of the shear layer separating from a bluff body. J. Fluid Mech. 333, 375–402.Google Scholar
Rai, M. M.2008 Towards direct numerical simulations of turbulent wakes. Paper 2008-0544, 46th AIAA Aerospace Sciences Meeting, 2008, Reno, NV.Google Scholar
Rai, M. M. 2010a A computational investigation of the instability of the detached shear layers in the wake of a circular cylinder. J. Fluid Mech. 659, 375–404.Google Scholar
Rai, M. M. 2010b Direct numerical simulation of transitional and turbulent flow on a turbine airfoil. AIAA J. Propul. Power 26 (3), 587–600.Google Scholar
Rai, M. M.2012 Phase-averaged Reynolds-stress budget in the turbulent near wake of a flat plate. Paper No. 2012-0067, 50th AIAA Aerospace Sciences Meeting, Nashville, TN.Google Scholar
Rai, M. M. 2013 Flow physics in the turbulent near wake of a flat plate. J. Fluid Mech. 724, 704–733.Google Scholar
Rai, M. M. 2014 Flow phenomena in the very near wake of a flat plate with a circular trailing edge. J. Fluid Mech. 756, 510–543.Google Scholar
Roshko, A.1953 On the development of turbulent wakes from vortex streets. NACA-TN-2913, NACA-TR-1191.Google Scholar
Thompson, M. C. & Hourigan, K. 2005 The shear layer instability of a cylinder wake. Phys. Fluids 17, 021702.Google Scholar
Townsend, A. A. 1966 The mechanism of entrainment in free turbulent flows. J. Fluid Mech. 26, 689–715.CrossRefGoogle Scholar
Unal, M. F. & Rockwell, D. 1988 On vortex formation from a cylinder. Part 1. The initial instability. J. Fluid Mech. 190, 491–512.Google Scholar