Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T22:27:32.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Density-ratio effects on the capture of suspended particles in aquatic systems

Published online by Cambridge University Press:  15 October 2015

Alexis Espinosa-Gayosso ,
Marco Ghisalberti ,
Gregory N. Ivey  and
Nicole L. Jones
Alexis Espinosa-Gayosso*
Affiliation:
Civil, Environmental and Mining Engineering, The University of Western Australia, Perth, WA 6009, Australia UWA Oceans Institute, The University of Western Australia, Perth, WA 6009, Australia
Marco Ghisalberti
Affiliation:
Civil, Environmental and Mining Engineering, The University of Western Australia, Perth, WA 6009, Australia
Gregory N. Ivey
Affiliation:
Civil, Environmental and Mining Engineering, The University of Western Australia, Perth, WA 6009, Australia UWA Oceans Institute, The University of Western Australia, Perth, WA 6009, Australia
Nicole L. Jones
Affiliation:
Civil, Environmental and Mining Engineering, The University of Western Australia, Perth, WA 6009, Australia UWA Oceans Institute, The University of Western Australia, Perth, WA 6009, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Particle capture, whereby suspended particles contact and adhere to a solid surface (a ‘collector’), is important in a range of environmental processes, including suspension feeding by corals and ‘filtering’ by aquatic vegetation. Although aquatic particles are often considered as perfect tracers when estimating capture efficiency, the particle density ratio (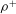${\it\rho}^{+}$) – the ratio of the particle density to the fluid density – can significantly affect capture. In this paper, we use a numerical analysis of particle trajectories to quantify the influence of 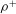${\it\rho}^{+}$ on particle capture by circular collectors in a parameter space relevant to aquatic systems. As it is generally believed that inertia augments the capture efficiency when the Stokes number (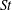$\mathit{St}$) of the particles exceeds a critical value, we first estimate the critical Stokes number for aquatic-type particles and demonstrate its dependence on both 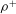${\it\rho}^{+}$ and the Reynolds number (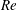$\mathit{Re}$). Second, we analyse how efficiently circular collectors can capture neutrally buoyant (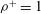${\it\rho}^{+}=1$), sediment-type (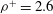${\it\rho}^{+}=2.6$) and weakly buoyant (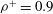${\it\rho}^{+}=0.9$) aquatic particles. Our analysis shows that, for 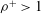${\it\rho}^{+}>1$, inertia can either augment or diminish capture efficiency, and inertial effects appear well before the critical Stokes number is reached. The role of particle inertia is maximised at Stokes numbers above the critical value and, for sediment-type particles, can result in as much as a fourfold increase in the rate of capture relative to perfect tracers of the same size. Similar but opposite effects are observed for weakly buoyant particles, where capture efficiency can decrease by 60 % relative to the capture of perfect tracers.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , pp. 191 - 210
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ackerman, J. D. 2006 Sexual reproduction of seagrasses: pollination in the marine context. In Seagrasses: Biology, Ecology and Conservation (ed. Larkum, A. W. D., Orth, R. J. & Duarte, C. M.), pp. 89–109. Springer.Google Scholar
Auton, T. R., Hunt, J. C. R. & Prudhomme, M. 1988 The force exerted on a body in inviscid unsteady non-uniform rotational flow. J. Fluid Mech. 197, 241–257.CrossRefGoogle Scholar
Babiano, A., Cartwright, J. H. E., Piro, O. & Provenzale, A. 2000 Dynamics of a small neutrally buoyant sphere in a fluid and targeting in Hamiltonian systems. Phys. Rev. Lett. 84 (25), 5764–5767.Google Scholar
Borowitzka, M. A. & Lethbridge, R. C. 1989 Seagrass epiphytes. In Biology of Seagrasses (ed. Shepherd, S. A., Larkum, A. W. D. & McComb, A. J.), pp. 458–498. Elsevier.Google Scholar
Brandon, D. J. & Aggarwal, S. K. 2001 A numerical investigation of particle deposition on a square cylinder placed in a channel flow. Aerosol Sci. Technol. 34 (4), 340–352.CrossRefGoogle Scholar
Davies, C. N. & Peetz, C. V. 1956 Impingement of particles on a transverse cylinder. Proc. R. Soc. Lond. A 234 (1197), 268–295.Google Scholar
Dormand, J. R. & Prince, P. J. 1980 A family of embedded Runge–Kutta formulae. J. Comput. Appl. Maths 6 (1), 19–26.Google Scholar
Espinosa-Gayosso, A., Ghisalberti, M., Ivey, G. N. & Jones, N. L. 2012 Particle capture and low-Reynolds-number flow around a circular cylinder. J. Fluid Mech. 710, 362–378.Google Scholar
Espinosa-Gayosso, A., Ghisalberti, M., Ivey, G. N. & Jones, N. L. 2013 Particle capture by a circular cylinder in the vortex-shedding regime. J. Fluid Mech. 733, 171–188.Google Scholar
Fernandez de la Mora, J. 1986 Inertia and interception in the deposition of particles from boundary-layers. Aerosol Sci. Technol. 5 (2), 261–286.CrossRefGoogle Scholar
Fernandez de la Mora, J. & Rosner, D. E. 1982 Effects of inertia on the diffusional deposition of small particles to spheres and cylinders at low Reynolds numbers. J. Fluid Mech. 125, 379–395.Google Scholar
Flagan, R. C. & Seinfeld, J. H. 1988 Fundamentals of Air Pollution Engineering, 1st edn. Prentice-Hall.Google Scholar
Friedlander, S. K. 2000 Smoke, dust and haze. In Fundamentals of Aerosol Dynamics, 2nd edn. Oxford University Press.Google Scholar
Fuchs, N. A. 1964 The Mechanics of Aerosols, 1st edn. Pergamon.Google Scholar
Haller, G. & Sapsis, T. 2008 Where do inertial particles go in fluid flows? Physica D 237 (5), 573–583.CrossRefGoogle Scholar
Harvey, M., Bourget, E. & Ingram, R. G. 1995 Experimental evidence of passive accumulation of marine bivalve larvae on filamentous epibenthic structures. Limnol. Oceanogr. 40 (1), 94–104.CrossRefGoogle Scholar
Haugen, N. E. L. & Kragset, S. 2010 Particle impaction on a cylinder in a crossflow as function of Stokes and Reynolds numbers. J. Fluid Mech. 661, 239–261.Google Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.Google Scholar
Hinds, W. C. 1982 Aerosol technology. In Properties, Behavior, and Measurement of Airborne Particles, 1st edn. John Wiley and Sons.Google Scholar
Langmuir, I. 1948 The production of rain by a chain reaction in cumulus clouds at temperatures above freezing. J. Meteorol. 5 (5), 175–192.Google Scholar
Lesnic, D., Elliott, L. & Ingham, D. B. 1994 Characterizations of the critical Stokes number for potential and viscous flows. Mathematika 41 (82), 277–292.Google Scholar
MathWorks2013 Matlab Release 2013b, The Mathworks Inc., Natick, MA, USA.Google Scholar
Matsufuji, H. & Hasegawa, E. 1986 Critical condition for collision of suspended small particles with a body in a viscous-fluid. Bull. JSME 29 (256), 3375–3382.Google Scholar
Maxey, M. R. 1987 The motion of small spherical particles in a cellular flow field. Phys. Fluids 30 (7), 1915–1928.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.Google Scholar
Michael, D. H. 1968 The steady motion of a sphere in a dusty gas. J. Fluid Mech. 31 (1), 175–192.Google Scholar
OpenCFD 2012 OpenCFD Lt, the producer of OpenFOAM software. http://www.openfoam.com/.Google Scholar
Palmer, M. R., Nepf, H. M., Pettersson, T. J. R. & Ackerman, J. D. 2004 Observations of particle capture on a cylindrical collector: implications for particle accumulation and removal in aquatic systems. Limnol. Oceanogr. 49 (1), 76–85.Google Scholar
Peruzzo, P., Defina, A., Nepf, H. M. & Stocker, R. 2013 Capillary interception of floating particles by surface-piercing vegetation. Phys. Rev. Lett. 111 (16), 164501, 1–5.Google Scholar
Phillips, C. G. & Kaye, S. R. 1999 The influence of the viscous boundary layer on the critical Stokes number for particle impaction near a stagnation point. J. Aerosol Sci. 30 (6), 709–718.Google Scholar
Robinson, A. 1956 On the motion of small particles in a potential field of flow. Commun. Pure Appl. Maths 9 (1), 69–84.Google Scholar
Shimeta, J. 1993 Diffusional encounter of submicrometer particles and small-cells by suspension feeders. Limnol. Oceanogr. 38 (2), 456–465.Google Scholar
Shimeta, J. & Jumars, P. A. 1991 Physical mechanisms and rates of particle capture by suspension-feeders. Oceanogr. Mar. Biol. 29, 191–257.Google Scholar
Shimeta, J. & Koehl, M. A. R. 1997 Mechanisms of particle selection by tentaculate suspension feeders during encounter, retention, and handling. J. Exp. Mar. Biol. Ecol. 209 (1–2), 47–73.Google Scholar
Taylor, G. I.1940 Note on possible equipment and technique for experiments on icing on aircraft Reports and Memoranda of the Aeronautical Research Committee (no. 2024) Ministry of Supply, Britain.Google Scholar
Weller, H. G., Tabor, G., Jasak, H. & Fureby, C. 1998 A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 12 (6), 620–631.Google Scholar
Wessel, R. A. & Righi, J. 1988 Generalized correlations for inertial impaction of particles on a circular-cylinder. Aerosol Sci. Technol. 9 (1), 29–60.Google Scholar
White, F. M. 2008 Fluid Mechanics, 6th edn. McGraw-Hill.Google Scholar
Wildish, D. & Kristmanson, D. 1997 Benthic Suspension Feeders and Flow, 1st edn. Cambridge University Press.Google Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders. Fundamentals, vol. 1. Oxford University Press.Google Scholar