Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T13:33:26.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Deformation of a spherical capsule under oscillating shear flow

Published online by Cambridge University Press:  02 December 2014

D. Matsunaga ,
Y. Imai ,
T. Yamaguchi  and
T. Ishikawa
D. Matsunaga
Affiliation:
Department of Bioengineering and Robotics, Tohoku University, 6-6-01 Aoba, Aoba, Sendai 980-8579, Japan
Y. Imai*
Affiliation:
Department of Bioengineering and Robotics, Tohoku University, 6-6-01 Aoba, Aoba, Sendai 980-8579, Japan
T. Yamaguchi
Affiliation:
Department of Biomedical Engineering, Tohoku University, 6-6-01 Aoba, Aoba, Sendai 980-8579, Japan
T. Ishikawa
Affiliation:
Department of Bioengineering and Robotics, Tohoku University, 6-6-01 Aoba, Aoba, Sendai 980-8579, Japan Department of Biomedical Engineering, Tohoku University, 6-6-01 Aoba, Aoba, Sendai 980-8579, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The deformation of a spherical capsule in oscillating shear flow is presented. The boundary element method is used to simulate the capsule motion under Stokes flow. We show that a capsule at high frequencies follows the deformation given by a leading-order prediction, which is derived from an assumption of small deformation limit. At low frequencies, on the other hand, a capsule shows an overshoot phenomenon where the maximum deformation is larger than that in steady shear flow. A larger overshoot is observed for larger capillary number or viscosity ratio. Using the maximum deformation in start-up shear flow, we evaluate the upper limit of deformation in oscillating shear flow. 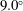We also show that the overshoot phenomenon may appear when the quasi-steady orientation angle under steady shear flow is less than $9.0^{\circ }$. We propose an equation to estimate the threshold frequency between the low-frequency range, where the capsule may have an overshoot, and the high-frequency range, where the deformation is given by the leading-order prediction. The equation only includes the viscosity ratio and the Taylor parameter under simple shear flow, so it can be extended to other deformable particles, such as bubbles and drops.

JFM classification

Low-Reynolds-number flows: Boundary integral methods Biological Fluid Dynamics: Capsule/cell dynamics Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , pp. 288 - 301
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babcock, H. P., Smith, D. E., Hur, J. S., Shaqfeh, E. S. G. & Chu, S. 2000 Relating the microscopic and macroscopic response of a polymeric fluid in a shearing flow. Phys. Rev. Lett. 85, 2018–2021.CrossRefGoogle Scholar
Bagchi, P. & Kalluri, R. M. 2011 Dynamic rheology of a dilute suspension of elastic capsules: effect of capsule tank-treading, swinging and tumbling. J. Fluid Mech. 669, 498–526.Google Scholar
Barthès-Biesel, D., Diaz, A. & Dhenin, E. 2002 Effect of constitutive laws for two-dimensional membranes on flow-induced capsule deformation. J. Fluid Mech. 460, 211–222.Google Scholar
Barthès-Biesel, D. & Rallison, J. M. 1981 The time-dependent deformation of a capsule freely suspended in a linear shear flow. J. Fluid Mech. 113, 251–267.Google Scholar
Barthès-Biesel, D. & Sgaier, H. 1985 Role of membrane viscosity in the orientation and deformation of a spherical capsule suspended in shear flow. J. Fluid Mech. 160, 119–135.Google Scholar
Cavallo, R., Guido, S. & Simeone, M. 2003 Drop deformation under small-amplitude oscillatory shear flow. Rheol. Acta 42 (1–2), 1–9.Google Scholar
Cox, R. G. 1969 The deformation of a drop in a general time-dependent fluid flow. J. Fluid Mech. 37, 601–623.Google Scholar
Doyle, S. P. & Shaqfeh, E. S. G. 1998 Dynamic simulation of freely-draining, flexible bead-rod chains: start-up of extensional and shear flow. J. Non-Newtonian Fluid Mech. 76 (1–3), 43–78.Google Scholar
Dupire, J., Abkarian, M. & Viallat, A. 2010 Chaotic dynamics of red blood cells in a sinusoidal flow. Phys. Rev. Lett. 104, 168101.Google Scholar
Foessel, É., Walter, J., Salsac, A.-V. & Barthès-Biesel, D. 2011 Influence of internal viscosity on the large deformation and buckling of a spherical capsule in a simple shear flow. J. Fluid Mech. 672, 477–486.Google Scholar
Frankel, N. A. & Acrivos, A. 1970 The constitutive equation for a dilute emulsion. J. Fluid Mech. 44, 65–78.Google Scholar
Kessler, S., Finken, R. & Seifert, U. 2008 Swinging and tumbling of elastic capsules in shear flow. J. Fluid Mech. 605, 207–226.Google Scholar
Lac, E., Barthès-Biesel, D., Pelekasis, N. A. & Tsamopoulos, J. 2004 Spherical capsules in three-dimensional unbounded stokes flows: effect of the membrane constitutive law and onset of buckling. J. Fluid Mech. 516, 303–334.Google Scholar
Li, X. & Sarkar, K. 2005a Drop dynamics in an oscillating extensional flow at finite Reynolds numbers. Phys. Fluids 17 (2), 027103.Google Scholar
Li, X. & Sarkar, K. 2005b Numerical investigation of the rheology of a dilute emulsion of drops in an oscillating extensional flow. J. Non-Newtonian Fluid Mech. 128 (2–3), 71–82.Google Scholar
Matsunaga, D., Imai, Y., Omori, T., Ishikawa, T. & Yamaguchi, T. 2014 A full GPU implementation of a numerical method for simulating capsule suspensions. J. Biomech. Sci. Engng. doi:10.1299/jbse.14-00039 (in press).Google Scholar
Palierne, J. F. 1990 Linear rheology of viscoelastic emulsions with interfacial tension. Rheol. Acta 29 (3), 204–214.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Pozrikidis, C. 1995 Finite deformation of liquid capsules enclosed by elastic membranes in simple shear flow. J. Fluid Mech. 297, 123–152.CrossRefGoogle Scholar
Pozrikidis, C. 2003 Modeling and Simulation of Capsules and Biological Cells. Chapman & Hall/CRC.Google Scholar
Ramanujan, S. & Pozrikidis, C. 1998 Deformation of liquid capsules enclosed by elastic membranes in simple shear flow: large deformations and the effect of fluid viscosities. J. Fluid Mech. 361, 117–143.Google Scholar
Sarkar, K. & Schowalter, W. R. 2001a Deformation of a two-dimensional drop at non-zero Reynolds number in time-periodic extensional flows: numerical simulation. J. Fluid Mech. 436, 177–206.Google Scholar
Sarkar, K. & Schowalter, W. R. 2001b Deformation of a two-dimensional viscous drop in time-periodic extensional flows: analytical treatment. J. Fluid Mech. 436, 207–230.CrossRefGoogle Scholar
Sibillo, V., Simeone, M. & Guido, S. 2004 Break-up of a newtonian drop in a viscoelastic matrix under simple shear flow. Rheol. Acta 43 (5), 449–456.Google Scholar
Walter, J., Salsac, A.-V. & Barthès-Biesel, D. 2011 Ellipsoidal capsules in simple shear flow: prolate versus oblate initial shapes. J. Fluid Mech. 676, 318–347.Google Scholar
Walter, J., Salsac, A.-V., Barthès-Biesel, D. & Le Tallec, P. 2010 Coupling of finite element and boundary integral methods for a capsule in a Stokes flow. Intl J. Numer. Meth. Engng 83 (7), 829–850.Google Scholar
Zhao, M. & Bagchi, P. 2011 Dynamics of microcapsules in oscillating shear flow. Phys. Fluids 23 (11), 111901.Google Scholar