Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T19:04:17.331Z Has data issue: false hasContentIssue false
  • English
  • Français

Deformation and sorting of capsules in a T-junction

Published online by Cambridge University Press:  17 December 2019

Edgar Häner ,
Matthias Heil Open the ORCID record for Matthias Heil [Opens in a new window]  and
Anne Juel Open the ORCID record for Anne Juel [Opens in a new window]
Edgar Häner
Affiliation:
MCND and Department of Physics and Astronomy, University of Manchester, Oxford Road, Manchester M13 9PL, UK
Matthias Heil
Affiliation:
Department of Mathematics and MCND, University of Mathematics, Oxford Road, Manchester M13 9PL, UK
Anne Juel*
Affiliation:
MCND and Department of Physics and Astronomy, University of Manchester, Oxford Road, Manchester M13 9PL, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

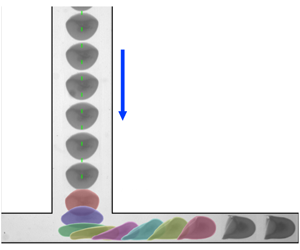
We study experimentally the motion and deformation of individual capsules transported by a constant volume-flux flow of low Reynolds number, through the T-junction of a channel with rectangular cross-section. We use millimetric ovalbumin-alginate capsules which we characterise independently of the flow experiment. Centred capsules travel at constant velocity down the straight channel leading to the T-junction, where they decelerate and expand in the spanwise direction before turning into one of the two identical daughter channels. There, non-inertial lift forces act to re-centre them and relax their shape until they reach a steady state of propagation. We find that the dynamics of fixed-size capsules within our channel geometry is governed by a capillary number $Ca$ defined as the ratio of viscous shear forces to elastic restoring forces, which we quantify by statically compressing the capsule between parallel plates to 50 % of its initial diameter, in order to account for different membrane thickness, pre-inflation and nonlinear elastic deformation. We show that the maximum extension in the T-junction of capsules of different stiffness collapses onto a master curve in $Ca$. This provides a sensitive measure of the relative stiffness of capsules at constant flow rate, particularly for softer capsules. We also find that the T-junction can sort fixed-size capsules according to their stiffness because the position in the T-junction from which capsules are entrained into the daughter channel depends uniquely on $Ca$. We demonstrate that a T-junction can be used as a sorting device by enhancing this initial capsule separation through a diffuser.

JFM classification

Biological Fluid Dynamics: Capsule/cell dynamics Biological Fluid Dynamics: Membranes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , A4
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abkarian, M., Faivre, M., Horton, R., Smistrup, K., Best-Popescu, C. A. & Stone, H. A. 2008 Cellular-scale hydrodynamics. Biomed. Mater. 3 (3), 034011.CrossRefGoogle ScholarPubMed
Al Quddus, N., Moussa, W. A. & Bhattacharjee, S. 2008 Motion of a spherical particle in a cylindrical channel using arbitrary Lagrangian–Eulerian method. J. Colloid Interface Sci. 317 (2), 620–630.CrossRefGoogle Scholar
Balogh, P. & Bagchi, P. 2018 Analysis of red blood cell partitioning at bifurcations in simulated microvascular networks. Phys. Fluids 30, 051902.CrossRefGoogle Scholar
Barthès-Biesel, D. 2016 Motion and deformation of elastic capsules and vesicles in flow. Annu. Rev. Fluid Mech. 48, 25–52.CrossRefGoogle Scholar
Bow, H., Pivkin, I. V., Diez-Silva, M., Goldfless, S. J., Dao, M., Niles, J. C., Suresh, S. & Han, J. 2011 A microfabricated deformability-based flow cytometer with application to malaria. Lab on a Chip 11, 1065–1073.CrossRefGoogle ScholarPubMed
Canny, J. 1986 A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 8 (6), 679–698.CrossRefGoogle ScholarPubMed
Carin, M., Barthès-Biesel, D., Edwards-Lévy, F., Postel, C. & Andrei, D. C. 2003 Compression of biocompatible liquid-filled HSA-alginate capsules: determination of the membrane mechanical properties. Biotechnol. Bioengng 82, 207–212.CrossRefGoogle ScholarPubMed
Chu, T.-X., Salsac, A.-V., Leclerc, E. & Barthès-Biesel, D. 2013 Automatic evaluation of the elastic modulus of a capsule membrane. In Advances in Intelligent and Soft Computing (ed. Huynh, V.-N., Denoeux, T., Tran, D. H., Le, A. C. & Pham, S. B.), vol. 2, pp. 389–398. Springer.Google Scholar
Cole, E. T., Cad, D. & Benameur, H. 2008 Challenges and opportunities in the encapsulation of liquid and semi-solid formulations into capsules for oral administration. Adv. Drug Deliv. Rev. 60, 747–756.CrossRefGoogle ScholarPubMed
Coupier, G., Kaoui, B., Podgorski, T. & Misbah, C. 2008 Noninertial lateral migration of vesicles in bounded Poiseuille flow. Phys. Fluids 20, 111702.CrossRefGoogle Scholar
Cupelli, C., Borchardt, T., Steiner, T., Paust, N., Zengerle, R. & Santer, M. 2013 Leukocyte enrichment based on a modified pinched flow fractionation approach. Microfluid. Nanofluid. 14 (3), 551–563.CrossRefGoogle Scholar
Dawson, G., Häner, E. & Juel, A. 2015 Extreme deformation of capsules and bubbles flowing through a localised constriction. Proc. IUTAM 16, 22–32.CrossRefGoogle Scholar
De Loubens, C., Deschamps, J., Boedec, G. & Leonetti, M. 2015 Stretching of capsules in an elongation flow, a route to constitutive law. J. Fluid Mech. 767, R3.CrossRefGoogle Scholar
De Loubens, C., Deschamps, J., Edwards-Levy, F. & Leonetti, M. 2016 Tank-treading of microcapsules in shear flow. J. Fluid Mech. 789, 750–767.CrossRefGoogle Scholar
De Loubens, C., Deschamps, J., Georgelin, M., Charrier, A., Edwards-Lévy, F. & Leonetti, M. 2014 Mechanical characterization of cross-linked serum albumin microcapsules. Soft Matt. 10 (25), 4561–4568.CrossRefGoogle ScholarPubMed
Di Carlo, D. 2009 Inertial microfluidics. Lab on a Chip 9 (21), 3038–3046.CrossRefGoogle ScholarPubMed
Doddi, S. K. & Bagchi, P. 2008 Lateral migration of a capsule in a plane Poiseuille flow in a channel. Intl J. Multiphase Flow 34, 966–986.CrossRefGoogle Scholar
Edwards-Lévy, F. & Lévy, M. C. 1999 Serum albumin–alginate coated beads: mechanical properties and stability. Biomaterials 20, 2069–2084.CrossRefGoogle ScholarPubMed
Fu, T., Ma, Y., Funfschilling, D. & Li, H. Z. 2011 Dynamics of bubble breakup in a microfluidic T-junction divergence. Chem. Engng Sci. 66 (18), 4184–4195.CrossRefGoogle Scholar
Geislinger, T. M. & Franke, T. 2013 Sorting of circulating tumor cells (MV3-melanoma) and red blood cells using non-inertial lift. Biomicrofluidics 7, 044120.CrossRefGoogle ScholarPubMed
Gubspun, J., de Loubens, C., Trozzo, R., Deschamps, J., Georgelin, M., Edwards-Levy, F. & Leonetti, M. 2017 Perturbations of the flow induced by a microcapsule in a capillary tube. Fluid Dyn. Res. 49, 035501.CrossRefGoogle Scholar
Häner, E.2017 Microfluidic segregation of capsules. PhD thesis, University of Manchester.Google Scholar
Hu, X.-Q., Salsac, A.-V. & Barthès-Biesel, D. 2012 Flow of a spherical capsule in a pore with circular or square cross-section. J. Fluid Mech. 705, 176–194.CrossRefGoogle Scholar
Hu, X.-Q., Sévénié, B., Salsac, A.-V., Leclerc, E. & Barthès-Biesel, D. 2013 Characterizing the membrane properties of capsules flowing in a square-section microfluidic channel: effects of the membrane constitutive law. Phys. Rev. E 87, 063008.Google Scholar
Huang, L. R., Cox, E. C., Austin, R. H. & Sturm, J. C. 2004 Continuous particle separation through deterministic lateral displacement. Science 304 (5673), 987–990.CrossRefGoogle ScholarPubMed
Hur, S. C., Henderson-MacLennan, N. K., McCabec, E. R. B. & Di Carlo, D. 2011 Deformability-based cell classification and enrichment using inertial microfluidics. Lab on a Chip 11, 912–920.CrossRefGoogle ScholarPubMed
Ilic, V., Tullock, D., Phan-Tien, N. & Graham, A. L. 1992 Translation and rotation of spheres settling in square and circular conduits: experiments and numerical predictions. Intl J. Multiphase Flow 18, 1061–1075.CrossRefGoogle Scholar
Jensen, O. E. & Chernyavsky, I. L. 2019 Blood flow and transport in the human placenta. Annu. Rev. Fluid Mech. 51, 25–47.CrossRefGoogle Scholar
Kabacaoǧlu, G. & Biros, G. 2019 Sorting same-size red blood cells in deep deterministic lateral displacement devices. J. Fluid Mech. 859, 433–475.CrossRefGoogle Scholar
Kaoui, B., Ristow, G. H., Cantat, I., Misbah, C. & Zimmermann, W. 2008 Lateral migration of a two-dimensional vesicle in unbounded Poiseuille flow. Phys. Rev. E 77, 021903.Google ScholarPubMed
Koolivand, A. & Dimitrakopoulos, P. 2017 Deformation of an elastic capsule in a microfluidic T-junction: settling shape and moduli determination. Microfluid. Nanofluid. 21 (5), 89.CrossRefGoogle Scholar
Kuriakose, S. & Dimitrakopoulos, P. 2011 Motion of an elastic capsule in a square microfluidic channel. Phys. Rev. E 84, 011906.Google Scholar
Kuriakose, S. & Dimitrakopoulos, P. 2013 Deformation of an elastic capsule in a rectangular microfluidic channel. Soft Matt. 9, 4284–4296.CrossRefGoogle Scholar
Lee, J. S., Dylla-Spears, R., Teclemariam, N. P. & Muller, S. J. 2007 Microfluidic four-roll mill for all flow types. Appl. Phys. Lett. 90 (7), 074103.Google Scholar
Lefebvre, Y., Leclerc, E., Barthès-Biesel, D., Walter, J. & Edwards-Lévy, F. 2008 Flow of artificial microcapsules in microfluidic channels: a method for determining the elastic properties of the membrane. Phys. Fluids 20, 123102.CrossRefGoogle Scholar
Lévy, M.-C. & Edwards-Lévy, F. 1996 Coating alginate beads with cross-linked biopolymers: a novel method based on a transacylation reaction. J. Microencapsul. 13 (2), 169–183.CrossRefGoogle ScholarPubMed
Lim, C. T. & Hoon, D. S. B. 2014 Circulating tumor cells: cancers deadly couriers. Phys. Today 67 (2), 26–30.CrossRefGoogle Scholar
Long, B. R., Heller, M., Beech, J. P., Linke, H., Bruus, H. & Tegenfeldt, J. O. 2008 Multidirectional sorting modes in deterministic lateral displacement devices. Phys. Rev. E 78 (4), 046304.Google ScholarPubMed
Otsu, N. 1979 A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 9 (1), 62–66.CrossRefGoogle Scholar
Popel, A. S. & Johnson, P. C. 2005 Microcirculation and hemorheology. Annu. Rev. Fluid Mech. 37, 43–69.CrossRefGoogle ScholarPubMed
Pozrikidis, C. 2005 Numerical simulation of cell motion in tube flow. Ann. Biomed. Engng 33 (2), 165–178.CrossRefGoogle ScholarPubMed
Pries, A. R., Secomb, T. W. & Gaehtgens, P. 1996 Biophysical aspects of blood flow in the microvasculature. Microvasc. Res. 32, 654–667.Google ScholarPubMed
Rabanel, J.-M., Banquy, X., Zouaoui, H., Mokhtar, M. & Hildgen, P. 2009 Progress technology in microencapsulation methods for cell therapy. Biotechnol. Prog. 25 (4), 946–963.CrossRefGoogle ScholarPubMed
Rachik, M., Barthès-Biesel, D., Carin, M. & Edwards-Lévy, F. 2006 Identification of the elastic properties of an artificial capsule membrane with the compression test: effect of thickness. J. Colloid Interface Sci. 301, 217–226.CrossRefGoogle ScholarPubMed
Risso, F. & Carin, M. 2004 Compression of a capsule: mechanical laws of membranes with negligible bending stiffness. Phys. Rev. E 69, 061601.Google ScholarPubMed
Risso, F., Collé-Paillot, F. & Zagzoule, M. 2006 Experimental investigation of a bioartificial capsule flowing in a narrow tube. J. Fluid Mech. 547, 149–173.CrossRefGoogle Scholar
Sajeesh, P. & Sen, A. K. 2014 Particle separation and sorting in microfluidic devices: a review. Microfluid. Nanofluid. 17 (1), 1–52.CrossRefGoogle Scholar
Vesperini, D., Chaput, O., Munier, N., Maire, P., Edwards-Lévy, F., Salsac, A.-V. & Le Goff, A. 2017 Deformability- and size-based microcapsule sorting. Med. Engng Phys. 48 (Suppl. C), 68–74.CrossRefGoogle ScholarPubMed
Villone, M. M. & Maffettone, P. L. 2019 Dynamics, rheology, and applications of elastic deformable particle suspensions: a review. Rheol. Acta 58, 109–130.CrossRefGoogle Scholar
Villone, M. M., Trofa, M., Hulsen, M. A. & Maffetone, P. L. 2017 Numerical design of a T-shaped microfluidic device for deformability-based separation of elastic capsules and soft beads. Phys. Rev. E 96, 053103.Google ScholarPubMed
Walter, J., Salsac, A.-V. & Barthès-Biesel, D. 2011 Ellipsoidal capsules in simple shear flow: prolate versus oblate initial shapes. J. Fluid Mech. 676, 318–347.CrossRefGoogle Scholar
Wang, Z., Sui, Y., Salsac, A.-V., Barthès-Biesel, D. & Wang, W. 2016 Motion of a spherical capsule in branched tube flow with finite inertia. J. Fluid Mech. 806, 603–626.CrossRefGoogle Scholar
Wang, Z., Sui, Y., Salsac, A.-V., Barthès-Biesel, D. & Wang, W. 2018 Path selection of a spherical capsule in a microfluidic branched channel: towards the design of an enrichment device. J. Fluid Mech. 849, 136–162.CrossRefGoogle Scholar
Woolfenden, H. C. & Blyth, M. G. 2011 Motion of a two-dimensional elastic capsule in a branching channel flow. J. Fluid Mech. 669, 3–31.CrossRefGoogle Scholar
Yamada, M., Nakashima, M. & Seki, M. 2004 Pinched flow fractionation: continuous size separation of particles utilizing a laminar flow profile in a pinched microchannel. Anal. Chem. 76 (18), 5465–5471.CrossRefGoogle Scholar
Zhu, L. & Brandt, L. 2015 The motion of a deforming capsule through a corner. J. Fluid Mech. 770, 374–397.CrossRefGoogle Scholar
Zhu, L., Rorai, C., Mitra, D. & Brand, L. 2014 A microfluidic device to sort capsules by deformability: a numerical study. Soft Matt. 10, 7705–7711.CrossRefGoogle ScholarPubMed