Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yan, Lei
Zhang, Xingming
Song, Jie
and
Hu, Gang
2024.
Active flow control of square cylinder adaptive to wind direction using deep reinforcement learning.
Physical Review Fluids,
Vol. 9,
Issue. 9,
Li, Xin
and
Deng, Jian
2024.
Active control of the flow past a circular cylinder using online dynamic mode decomposition.
Journal of Fluid Mechanics,
Vol. 997,
Issue. ,
Ren, Feng
Wen, Xin
and
Tang, Hui
2024.
Model-Free Closed-Loop Control of Flow Past a Bluff Body: Methods, Applications, and Emerging Trends.
Actuators,
Vol. 13,
Issue. 12,
p.
488.
Zhu, Qingchi
Zhou, Lei
Zhang, Hongfu
Tse, Kam Tim
Tang, Hui
and
Noack, Bernd R.
2024.
A zero-net-mass-flux wake stabilization method for blunt bodies via global linear instability.
Physics of Fluids,
Vol. 36,
Issue. 4,
Bai, Heming
Wang, Zhicheng
Chu, Xuesen
Deng, Jian
and
Bian, Xin
2024.
Data-driven modeling of unsteady flow based on deep operator network.
Physics of Fluids,
Vol. 36,
Issue. 6,
Zhao, Fuwang
Zeng, Lingwei
Bai, Honglei
Alam, Md. Mahbub
Wang, Zhaokun
Dong, You
and
Tang, Hui
2024.
Vortex-induced vibration of a sinusoidal wavy cylinder: The effect of wavelength.
Physics of Fluids,
Vol. 36,
Issue. 8,
Mao, Yiqian
Zhong, Shan
and
Yin, Hujun
2024.
Model-based deep reinforcement learning for active control of flow around a circular cylinder using action-informed episode-based neural ordinary differential equations.
Physics of Fluids,
Vol. 36,
Issue. 8,
Kim, Innyoung
Jeon, Youngmin
Chae, Jonghyun
and
You, Donghyun
2024.
Deep Reinforcement Learning for Fluid Mechanics: Control, Optimization, and Automation.
Fluids,
Vol. 9,
Issue. 9,
p.
216.
Wälchli, D
Guastoni, L
Vinuesa, R
and
Koumoutsakos, P
2024.
Drag reduction in a minimal channel flow with scientific multi-agent reinforcement learning.
Journal of Physics: Conference Series,
Vol. 2753,
Issue. 1,
p.
012024.
Chatzimanolakis, Michail
Weber, Pascal
and
Koumoutsakos, Petros
2024.
Learning in two dimensions and controlling in three: Generalizable drag reduction strategies for flows past circular cylinders through deep reinforcement learning.
Physical Review Fluids,
Vol. 9,
Issue. 4,
Ye, Mai
Ma, Hao
Ren, Yaru
Zhang, Chi
Haidn, Oskar J.
and
Hu, Xiangyu
2025.
DRLinSPH: an open-source platform using deep reinforcement learning and SPHinXsys for fluid-structure-interaction problems.
Engineering Applications of Computational Fluid Mechanics,
Vol. 19,
Issue. 1,
Font, Bernat
Alcántara-Ávila, Francisco
Rabault, Jean
Vinuesa, Ricardo
and
Lehmkuhl, Oriol
2025.
Deep reinforcement learning for active flow control in a turbulent separation bubble.
Nature Communications,
Vol. 16,
Issue. 1,
Chen, Jingbo
Ballini, Enrico
and
Micheletti, Stefano
2025.
Active flow control for bluff body under high Reynolds number turbulent flow conditions using deep reinforcement learning.
Physics of Fluids,
Vol. 37,
Issue. 2,
Gao, Chuanqiang
Yang, Xinyu
Ren, Kai
and
Zhang, Weiwei
2025.
Open-loop linear modeling method for unstable flow utilizing built-in data-driven feedback controllers.
Physical Review Fluids,
Vol. 10,
Issue. 3,
Gong, Maojin
and
Dally, Bassam
2025.
A review of flow-induced vibration in wind and oceanic flow: Mechanisms, applications, optimizations, and challenges.
Ocean Engineering,
Vol. 325,
Issue. ,
p.
120748.
Omichi, Hiroshi
Linot, Alec J.
Fukagata, Koji
and
Taira, Kunihiko
2025.
Reinforcement Learning With Symmetry Reduction for Rotating Cylinder Wakes: Finding Unstable Low-Drag Fixed Points.
Yan, Lei
Wang, Qiulei
Hu, Gang
Chen, Wenli
and
Noack, Bernd R.
2025.
Deep reinforcement cross-domain transfer learning of active flow control for three-dimensional bluff body flow.
Journal of Computational Physics,
Vol. 529,
Issue. ,
p.
113893.
Suárez, Pol
Alcántara-Ávila, Francisco
Miró, Arnau
Rabault, Jean
Font, Bernat
Lehmkuhl, Oriol
and
Vinuesa, Ricardo
2025.
Active Flow Control for Drag Reduction Through Multi-agent Reinforcement Learning on a Turbulent Cylinder at $$Re_D=3900$$.
Flow, Turbulence and Combustion,
Yan, Lei
Cai, Huaiqiang
Wang, Qiulei
Chen, Lingwei
Li, Chao
and
Hu, Gang
2025.
Deep reinforcement learning-based active flow control for a tall building.
Physics of Fluids,
Vol. 37,
Issue. 4,
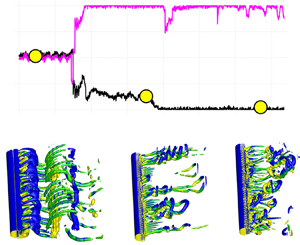
 $Re$) using transfer learning. We consider the canonical flow past a circular cylinder whose wake is controlled by two small rotating cylinders. We first pre-train the DRL agent using data from inexpensive simulations at low
$Re$) using transfer learning. We consider the canonical flow past a circular cylinder whose wake is controlled by two small rotating cylinders. We first pre-train the DRL agent using data from inexpensive simulations at low  $Re$, and subsequently we train the agent with small data from the simulation at high
$Re$, and subsequently we train the agent with small data from the simulation at high  $Re$ (up to
$Re$ (up to  $Re=1.4\times 10^5$). We apply transfer learning (TL) to three different tasks, the results of which show that TL can greatly reduce the training episodes, while the control method selected by TL is more stable compared with training DRL from scratch. We analyse for the first time the wake flow at
$Re=1.4\times 10^5$). We apply transfer learning (TL) to three different tasks, the results of which show that TL can greatly reduce the training episodes, while the control method selected by TL is more stable compared with training DRL from scratch. We analyse for the first time the wake flow at  $Re=1.4\times 10^5$ in detail and discover that the hydrodynamic forces on the two rotating control cylinders are not symmetric.
$Re=1.4\times 10^5$ in detail and discover that the hydrodynamic forces on the two rotating control cylinders are not symmetric.


