Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-17T19:07:50.949Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of fluid forcing and phase synchronisation for in-line vortex-induced vibration of a circular cylinder

Published online by Cambridge University Press:  12 May 2022

Jisheng Zhao Open the ORCID record for Jisheng Zhao [Opens in a new window] ,
Mark C. Thompson Open the ORCID record for Mark C. Thompson [Opens in a new window]  and
Kerry Hourigan Open the ORCID record for Kerry Hourigan [Opens in a new window]
Jisheng Zhao*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
Kerry Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

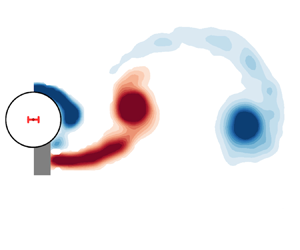
We present a decomposition of the streamwise fluid force for in-line vortex-induced vibration (VIV) to provide insight into how the wake drag acts as a driving force in fluid–structure interaction. This force decomposition is an extension of that proposed in the recent work of Konstantinidis et al. (J. Fluid Mech., vol. 907, 2021, p. A34), and is applied to and validated by our experiments examining a circular cylinder freely vibrating in line with the free stream. It is revealed from the decomposition and linear analysis that two regimes of significant vibration are in phase synchronisation, while they are separated by a desynchronised regime marked by competition between non-stationary frequency responses of the cylinder vibration and the vortex shedding. Of interest, such a near-resonance desynchronisation regime is not seen in the transverse vibration case.

JFM classification

Aerodynamics: Flow-structure interactions Vortex Flows: Vortex dynamics Wakes/Jets: Wakes
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 941 , 25 June 2022 , R4
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aguirre, J.E. 1977 Flow-induced in-line vibrations of a circular cylinder. PhD thesis, Imperial College of Science and Technology.Google Scholar
Bourguet, R. & Lo Jacono, D. 2015 In-line flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 781, 127–165.CrossRefGoogle Scholar
Cagney, N. & Balabani, S. 2013 a Mode competition in streamwise-only vortex induced vibrations. J. Fluids Struct. 41, 156–165.CrossRefGoogle Scholar
Cagney, N. & Balabani, S. 2013 b Wake modes of a cylinder undergoing free streamwise vortex-induced vibrations. J. Fluids Struct. 38, 127–145.CrossRefGoogle Scholar
Govardhan, R. & Williamson, C.H.K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.CrossRefGoogle Scholar
Gurian, T.D., Currier, T. & Modarres-Sadeghi, Y. 2019 Flow force measurements and the wake transition in purely inline vortex-induced vibration of a circular cylinder. Phys. Rev. Fluids 4, 034701.CrossRefGoogle Scholar
Konstantinidis, E. 2014 On the response and wake modes of a cylinder undergoing streamwise vortex-induced vibration. J. Fluids Struct. 45, 256–262.CrossRefGoogle Scholar
Konstantinidis, E. & Bouris, D. 2017 Drag and inertia coefficients for a circular cylinder in steady plus low-amplitude oscillatory flows. Appl. Ocean Res. 65, 219–228.CrossRefGoogle Scholar
Konstantinidis, E., Dorogi, D. & Baranyi, L. 2021 Resonance in vortex-induced in-line vibration at low Reynolds numbers. J. Fluid Mech. 907, A34.CrossRefGoogle Scholar
Lighthill, J. 1986 Fundamentals concerning wave loading on offshore structures. J. Fluid Mech. 173, 667–681.CrossRefGoogle Scholar
Limacher, E., Morton, C. & Wood, D. 2018 Generalized derivation of the added-mass and circulatory forces for viscous flows. Phys. Rev. Fluids 3 (1), 014701.CrossRefGoogle Scholar
Limacher, E.J. 2021 Added-mass force on elliptic airfoils. J. Fluid Mech. 926, R2.CrossRefGoogle Scholar
McQueen, T., Zhao, J., Sheridan, J. & Thompson, M.C. 2021 Vibration reduction of a sphere through shear-layer control. J. Fluids Struct. 105, 103325.CrossRefGoogle Scholar
Morison, J.R., Johnson, J.W. & Schaaf, S.A. 1950 The force exerted by surface waves on piles. Petrol. Trans. AIME 189, 149–154.Google Scholar
Nemes, A., Zhao, J., Lo Jacono, D. & Sheridan, J. 2012 The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack. J. Fluid Mech. 710, 102–130.CrossRefGoogle Scholar
Okajima, A., Nakamura, A., Kosugi, T., Uchida, H. & Tamaki, R. 2004 Flow-induced in-line oscillation of a circular cylinder. Eur. J. Mech. (B/Fluids) 23 (1), 115–125.CrossRefGoogle Scholar
Sareen, A., Zhao, J., Lo Jacono, D., Sheridan, J., Hourigan, K. & Thompson, M.C. 2018 Vortex-induced vibration of a rotating sphere. J. Fluid Mech. 837, 258–292.CrossRefGoogle Scholar
Soti, A.K., Zhao, J., Thompson, M.C., Sheridan, J. & Bhardwaj, R. 2018 Damping effects on vortex-induced vibration of a circular cylinder and implications for power extraction. J. Fluids Struct. 81, 289–308.CrossRefGoogle Scholar
Wong, K.W.L., Zhao, J., Lo Jacono, D., Thompson, M.C. & Sheridan, J. 2018 Experimental investigation of flow-induced vibration of a sinusoidally rotating circular cylinder. J. Fluid Mech. 848, 430–466.CrossRefGoogle Scholar
Zhao, J., Hourigan, K. & Thompson, M.C. 2018 a Flow-induced vibration of D-section cylinders: an afterbody is not essential for vortex-induced vibration. J. Fluid Mech. 851, 317–343.CrossRefGoogle Scholar
Zhao, J., Hourigan, K. & Thompson, M.C. 2019 An experimental investigation of flow-induced vibration of high-side-ratio rectangular cylinders. J. Fluids Struct. 91, 102580.CrossRefGoogle Scholar
Zhao, J., Leontini, J.S., Lo Jacono, D. & Sheridan, J. 2014 Fluid–structure interaction of a square cylinder at different angles of attack. J. Fluid Mech. 747, 688–721.CrossRefGoogle Scholar
Zhao, J., Lo Jacono, D., Sheridan, J., Hourigan, K. & Thompson, M.C. 2018 b Experimental investigation of in-line flow-induced vibration of a rotating cylinder. J. Fluid Mech. 847, 664–699.CrossRefGoogle Scholar
Zhao, J., Nemes, A., Lo Jacono, D. & Sheridan, J. 2018 c Branch/mode competition in the flow-induced vibration of a square cylinder. Phil. Trans. R. Soc. Lond. A 376, 20170243.Google ScholarPubMed

Zhao et al. supplementary movie 1

Phase-averaged vorticity contours showing the wake evolutions at U* = [1.60, 1.80, 2.00, 2.15, 2.25, 2.30, 2.40] in regime I.

Download Zhao et al. supplementary movie 1(Video)
Video 5.6 MB

Zhao et al. supplementary movie 2

Phase-averaged vorticity contours showing the wake evolutions at U* = 2.55 (in the competing region) and 4.80 (in the desynchronisation region).

Download Zhao et al. supplementary movie 2(Video)
Video 2.7 MB

Zhao et al. supplementary movie 3

Phase-averaged vorticity contours showing the wake evolutions at U* = [3.00, 3.50, 4.20] in regime II.

Download Zhao et al. supplementary movie 3(Video)
Video 2.4 MB