Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hamid, Ahmad H. A.
Hussam, Wisam K.
and
Sheard, Gregory J.
2016.
Heat transfer augmentation of a quasi-two-dimensional MHD duct flow via electrically driven vortices.
Numerical Heat Transfer, Part A: Applications,
Vol. 70,
Issue. 8,
p.
847.
Hamid, Ahmad H. A.
Hussam, Wisam K.
and
Sheard, Gregory J.
2016.
Combining an obstacle and electrically driven vortices to enhance heat transfer in a quasi-two-dimensional MHD duct flow.
Journal of Fluid Mechanics,
Vol. 792,
Issue. ,
p.
364.
Baker, Nathaniel T.
Pothérat, Alban
Davoust, Laurent
Debray, François
and
Klein, Rico
2017.
Controlling the dimensionality of low-Rm MHD turbulence experimentally.
Experiments in Fluids,
Vol. 58,
Issue. 7,
Pothérat, Alban
and
Klein, Rico
2017.
Do magnetic fields enhance turbulence at low magnetic Reynolds number?.
Physical Review Fluids,
Vol. 2,
Issue. 6,
Zhai, X. M.
and
Yeung, P. K.
2018.
Evolution of anisotropy in direct numerical simulations of MHD turbulence in a strong magnetic field on elongated periodic domains.
Physical Review Fluids,
Vol. 3,
Issue. 8,
Baker, Nathaniel T.
Pothérat, Alban
Davoust, Laurent
and
Debray, François
2018.
Inverse and Direct Energy Cascades in Three-Dimensional Magnetohydrodynamic Turbulence at Low Magnetic Reynolds Number.
Physical Review Letters,
Vol. 120,
Issue. 22,
Moriconi, L.
2020.
Magnetic dissipation of near-wall turbulent coherent structures in magnetohydrodynamic pipe flows.
Physical Review E,
Vol. 101,
Issue. 4,
Moudjed, B.
Pothérat, A.
and
Holdsworth, M.
2020.
PIV mapping of pressure and velocity fields in the plane magnetohydrodynamic Couette flow.
Experiments in Fluids,
Vol. 61,
Issue. 12,
Doche, Olivier
Tardu, Sedat
Schillings, Jonathan
and
Capogna, Amandine
2021.
Transportation and coherent structures in MHD turbulent channel flow subject to uniform streamwise and spanwise magnetic fields.
Physical Review Fluids,
Vol. 6,
Issue. 9,
Krasnov, D.
Listratov, Ya.
Kolesnikov, Yu.
Belyaev, I.
Pyatnitskaya, N.
Sviridov, E.
and
Zikanov, O.
2021.
Transformation of a submerged flat jet under strong transverse magnetic field.
EPL (Europhysics Letters),
Vol. 134,
Issue. 2,
p.
24003.
Chen, Long
Pothérat, Alban
Ni, Ming-Jiu
and
Moreau, René
2021.
Direct numerical simulation of quasi-two-dimensional MHD turbulent shear flows.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Camobreco, Christopher J.
Pothérat, Alban
and
Sheard, Gregory J.
2021.
Transition to turbulence in quasi-two-dimensional MHD flow driven by lateral walls.
Physical Review Fluids,
Vol. 6,
Issue. 1,
Camobreco, Christopher J.
Pothérat, Alban
and
Sheard, Gregory J.
2021.
Stability of pulsatile quasi-two-dimensional duct flows under a transverse magnetic field.
Physical Review Fluids,
Vol. 6,
Issue. 5,
Lai, Jun
Chen, Tao
Zhang, Shengqi
Xiao, Zuoli
Chen, Shiyi
and
Wang, Lian-Ping
2022.
A Systematic Study of a Droplet Breakup Process in Decaying Homogeneous Isotropic Turbulence Using a Mesoscopic Simulation Approach.
SSRN Electronic Journal,
Lai, Jun
Chen, Tao
Zhang, Shengqi
Xiao, Zuoli
Chen, Shiyi
and
Wang, Lian-Ping
2022.
A systematic study of a droplet breakup process in decaying homogeneous isotropic turbulence using a mesoscopic simulation approach.
Journal of Turbulence,
Vol. 23,
Issue. 11-12,
p.
567.
Sukoriansky, Semion
Barami, Eli
Feldman, Yuri
and
Zemach, Efi
2022.
Anisotropization of quasistatic magnetohydrodynamic turbulence with an increasing magnetic field: Transition from three to two dimensions.
Physical Review Fluids,
Vol. 7,
Issue. 7,
Fico, Francesco
Langella, Ivan
and
Xia, Hao
2023.
Large-eddy simulation of magnetohydrodynamics and heat transfer in annular pipe liquid metal flow.
Physics of Fluids,
Vol. 35,
Issue. 5,
Brynjell-Rahkola, Mattias
Duguet, Yohann
and
Boeck, Thomas
2024.
Chaotic edge regimes in magnetohydrodynamic channel flow: An alternative path towards the tipping point.
Physical Review Research,
Vol. 6,
Issue. 3,
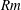 $Rm$
$Rm$


