Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-20T17:25:44.531Z Has data issue: false hasContentIssue false
  • English
  • Français

A data-assimilation method for Reynolds-averaged Navier–Stokes-driven mean flow reconstruction

Published online by Cambridge University Press:  04 November 2014

Dimitry P. G. Foures ,
Nicolas Dovetta ,
Denis Sipp  and
Peter J. Schmid
Dimitry P. G. Foures
Affiliation:
DAMTP, Centre for Mathematical Sciences, University of Cambridge, Cambridge CB3 0WA, UK
Nicolas Dovetta
Affiliation:
LadHyX, Ecole Polytechnique, 91128 Palaiseau, France
Denis Sipp*
Affiliation:
ONERA-DAFE, 8 rue des Vertugadins, 92190 Meudon, France
Peter J. Schmid
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a data-assimilation technique based on a variational formulation and a Lagrange multipliers approach to enforce the Navier–Stokes equations. A general operator (referred to as the measure operator) is defined in order to mathematically describe an experimental measure. The presented method is applied to the case of mean flow measurements. Such a flow can be described by the Reynolds-averaged Navier–Stokes (RANS) equations, which can be formulated as the classical Navier–Stokes equations driven by a forcing term involving the Reynolds stresses. The stress term is an unknown of the equations and is thus chosen as the control parameter in our study. The data-assimilation algorithm is derived to minimize the error between a mean flow measurement and the measure performed on a numerical solution of the steady, forced Navier–Stokes equations; the optimal forcing is found when this error is minimal. 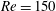We demonstrate the developed data-assimilation framework on a test case: the two-dimensional flow around an infinite cylinder at a Reynolds number of $\mathit{Re}=150$. The mean flow is computed by time-averaging instantaneous flow fields from a direct numerical simulation (DNS). We then perform several ‘measures’ on this mean flow and apply the data-assimilation method to reconstruct the full mean flow field. Spatial interpolation, extrapolation, state vector reconstruction and noise filtering are considered independently. The efficacy of the developed identification algorithm is quantified for each of these cases and compared with more traditional methods when possible. We also analyse the identified forcing in terms of unsteadiness characterization, present a way to recover the second-order statistical moments of the fluctuating velocities and finally explore the possibility of pressure reconstruction from velocity measurements.

JFM classification

Mathematical Foundations: General fluid mechanics Turbulent Flows: Turbulence modelling Mathematical Foundations: Variational methods
Type
Papers
Information
Journal of Fluid Mechanics , Volume 759 , 25 November 2014 , pp. 404 - 431
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avril, S., Bonnet, M., Bretelle, A.-S., Grédiac, M., Hild, F., Ienny, P., Latourte, F., Lemosse, D., Pagano, S., Pagnacco, E. & Pierron, F. 2008 Overview of identification methods of mechanical parameters based on full-field measurements. Exp. Mech. 48 (4), 381–402.CrossRefGoogle Scholar
Courtier, P. 1997 Dual formulation of four-dimensional variational assimilation. Q. J. R. Meteorol. Soc. 123 (544), 2449–2461.CrossRefGoogle Scholar
Everson, R. & Sirovich, L. 1995 Karhunen–Loeve procedure for gappy data. J. Opt. Soc. Amer. A 12 (8), 1657–1664.Google Scholar
Ghil, M. & Malanotte-Rizzoli, P. 1991 Data assimilation in meteorology and oceanography. Adv. Geophys. 33, 141–266.Google Scholar
Gunes, H., Sirisup, S. & Karniadakis, G. E. 2006 Gappy data: to krig or not to krig? J. Comput. Phys. 212 (1), 358–382.CrossRefGoogle Scholar
Gunzburger, M. D. 2000 Adjoint equation-based methods for control problems in incompressible, viscous flows. Flow Turbul. Combust. 65 (3–4), 249–272.CrossRefGoogle Scholar
Heitz, D., Mémin, E. & Schnorr, C. 2010 Variationnal fluid flow measurements from image sequences: synopsis and perspectives. Exp. Fluids 48 (3), 369–393.Google Scholar
Hill, D. C. 1995 Adjoint systems and their role in the receptivity problem for boundary layers. J. Fluid Mech. 292, 183–204.CrossRefGoogle Scholar
Jackson, C. P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182 (1), 23–45.CrossRefGoogle Scholar
Le Dimet, F.-X. & Talagrand, O. 1986 Variational algorithms for analysis and assimilation of meteorological observations: theoretical aspects. Tellus 38A, 97–110.Google Scholar
Luchini, P. & Bottaro, A. 2001 Linear stability and receptivity analyses of the stokes layer produced by an impulsively started plate. Phys. Fluids 13, 1668–1678.CrossRefGoogle Scholar
Lundvall, J., Kozlov, V. & Weinerfelt, P. 2006 Iterative methods for data assimilation for burgers’s equation. J. Inverse Ill-Posed Probl. 14 (5), 505–535.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of the cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Mohammadi, B. & Pironneau, O. 2004 Shape optimization in fluid mechanics. Annu. Rev. Fluid Mech. 36, 255–279.Google Scholar
Pralits, J., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
Ruhnau, P., Kohlberger, T., Nobach, H. & Schnorr, C. 2005 Variationnal optical flow estimation for particle image velocimetry. Exp. Fluids 38, 21–32.Google Scholar
Ruhnau, P. & Schnorr, C. 2007 Optical stokes flow estimation: an imaging-based control approach. Exp. Fluids 42, 61–78.CrossRefGoogle Scholar
Ruhnau, P., Stahl, A. & Schnorr, C. 2007 Variational estimation of experimental fluid flows with physics-based spatio-temporal regularization. Meas. Sci. Technol. 18, 755–763.CrossRefGoogle Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Sipp, D., Marquet, O., Meliga, Ph. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open flows: a linearized approach. Appl. Mech. Rev. 63, 030801.CrossRefGoogle Scholar