Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T18:27:06.865Z Has data issue: false hasContentIssue false
  • English
  • Français

Cylinder wakes in shallow oscillatory flow: the coastal island wake problem

Published online by Cambridge University Press:  04 July 2019

Paul M. Branson Open the ORCID record for Paul M. Branson [Opens in a new window] ,
Marco Ghisalberti Open the ORCID record for Marco Ghisalberti [Opens in a new window] ,
Gregory N. Ivey Open the ORCID record for Gregory N. Ivey [Opens in a new window]  and
Emil J. Hopfinger Open the ORCID record for Emil J. Hopfinger [Opens in a new window]
Paul M. Branson*
Affiliation:
Oceans Graduate School, University of Western Australia, Crawley, 6009, Australia
Marco Ghisalberti
Affiliation:
Oceans Graduate School, University of Western Australia, Crawley, 6009, Australia
Gregory N. Ivey
Affiliation:
Oceans Graduate School, University of Western Australia, Crawley, 6009, Australia
Emil J. Hopfinger
Affiliation:
LEGI, CNRS/UGA, Grenoble, 38400, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Topographic complexity on continental shelves is the catalyst that transforms the barotropic tide into the secondary and residual circulations that dominate vertical and cross-shelf mixing processes. Island wakes are one such example that are observed to significantly influence the transport and distribution of biological and physical scalars. Despite the importance of island wakes, to date, no sufficient, mechanistic description of the physical processes governing their development exists for the general case of unsteady tidal forcing. Controlled laboratory experiments are necessary for the understanding of this complex flow phenomenon. Here, three-dimensional velocity field measurements of cylinder wakes in shallow-water oscillatory flow are conducted across a parameter space that is typical of tidal flow around shallow islands. The wake form in steady flows is typically described in terms of the stability parameter 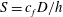$S=c_{f}D/h$ (where 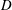$D$ is the island diameter, 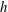$h$ is the water depth and 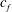$c_{f}$ is the bottom boundary friction coefficient); in tidal flows, there is an additional dependence on the Keulegan–Carpenter number 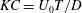$KC=U_{0}T/D$ (where 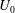$U_{0}$ is the tidal velocity amplitude and 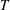$T$ is the tidal period). In this study we demonstrate that when the influence of bottom friction is confined to a Stokes boundary layer the stability parameter is given by 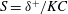$S=\unicode[STIX]{x1D6FF}^{+}/KC$ where 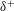$\unicode[STIX]{x1D6FF}^{+}$ is the ratio of the wavelength of the Stokes bottom boundary layer to the depth. Three classes of wake form are observed with decreasing wake stability: (i) steady bubble for 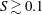$S\gtrsim 0.1$; (ii) unsteady bubble for 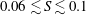$0.06\lesssim S\lesssim 0.1$; and (iii) vortex shedding for 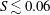$S\lesssim 0.06$. Transitions in wake form and wake stability are shown to depend on the magnitude and temporal evolution of the wake return flow. Scaling laws are developed to allow upscaling of the laboratory results to island wakes. Vertical and lateral transport depend on three parameters: (i) the flow aspect ratio 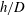$h/D$; (ii) the amplitude of tidal motion relative to the island size, given by 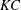$KC$; and (iii) the relative influence of bottom friction to the flow depth, given by 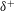$\unicode[STIX]{x1D6FF}^{+}$. A model of wake upwelling based on Ekman pumping from the bottom boundary layer demonstrates that upwelling in the near-wake region of an island scales with 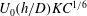$U_{0}(h/D)KC^{1/6}$ and is independent of the wake form. Finally, we demonstrate an intrinsic link between the dynamical eddy scales, predicted by the Ekman pumping model, and the island wake form and stability.

JFM classification

Geophysical and Geological Flows: Shallow water flows Geophysical and Geological Flows: Topographic effects Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 158 - 184
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akkermans, R. A. D., Cieslik, A. R., Kamp, L. P. J., Trieling, R. R., Clercx, H. J. H. & van Heijst, G. J. F. 2008 The three-dimensional structure of an electromagnetically generated dipolar vortex in a shallow fluid layer. Phys. Fluids 20, 116601.10.1063/1.3005452Google Scholar
Atkinson, C., Coudert, S., Foucaut, J., Stanislas, M. & Soria, J. 2010 The accuracy of tomographic particle image velocimetry for measurements of a turbulent boundary layer. Exp. Fluids 50 (4), 1031–1056.Google Scholar
Batchelor, G. K. 2000 An Introduction to Fluid Dynamics (Cambridge Mathematical Library). Cambridge University Press.10.1017/CBO9780511800955Google Scholar
Belden, J. 2013 Calibration of multi-camera systems with refractive interfaces. Exp. Fluids 54 (2), 1–18.Google Scholar
Belden, J., Truscott, T. T., Axiak, M. C. & Techet, A. H. 2010 Three-dimensional synthetic aperture particle image velocimetry. Meas. Sci. Technol. 21 (12), 125403.10.1088/0957-0233/21/12/125403Google Scholar
Branson, P. M.2018 Laboratory study of circulation and upwelling in tidally-forced, shallow water island wakes. PhD thesis, Oceans Graduate School, University of Western Australia.Google Scholar
Branson, P. M., Ghisalberti, M. & Ivey, G. N. 2019 Three-dimensionality of shallow island wakes. Environ. Fluid Mech. doi:10.1007/s10652-019-09661-5.Google Scholar
Chen, D. & Jirka, G. H. 1995 Experimental study of plane turbulent wakes in a shallow water layer. Fluid Dyn. Res. 16 (1), 11–41.Google Scholar
Chen, D. & Jirka, G. H. 1997 Absolute and convective instabilities of plane turbulent wakes in a shallow water layer. J. Fluid Mech. 338, 157–172.10.1017/S0022112097005041Google Scholar
Chu, V. H., Wu, J. H. & Khayat, R. E. 1983 Stability of turbulent shear flows in shallow channel. In Proceeding of the 20th Congress of IAHR, Moscow, pp. 128–133. International Association for Hydraulic Research.Google Scholar
Creswell, G. R. & Badcock, K. A. 2000 Tidal mixing near the kimberley coast of NW Australia. Mar. Freshwat. Res. 51, 641–646.Google Scholar
Cushman-Roisin, B. & Beckers, J. 2011 Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects, International Geophysics, vol. 101. Academic Press.Google Scholar
Delandmeter, P., Lambrechts, J., Marmorino, G. O., Legat, V., Wolanski, E., Remacle, J., Chen, W. & Deleersnijder, E. 2017 Submesoscale tidal eddies in the wake of coral islands and reefs: satellite data and numerical modelling. Ocean Dyn. 67 (7), 897–913.Google Scholar
Duran-Matute, M., Kamp, L. P. J., Trieling, R. R. & van Heijst, G. J. F. 2012 Regimes of two-dimensionality of decaying shallow axisymmetric swirl flows with background rotation. J. Fluid Mech. 691, 214–244.Google Scholar
Earl, T. A., Paetzold, J. & Cochard, S. 2013 Tomographic PIV measurements of turbulent fountains with refraction index matching. J. Flow Visualization Image Process. 20 (3), 179–208.Google Scholar
Fischer, H. B. 1973 Longitudinal dispersion and turbulent mixing in open-channel flow. Annu. Rev. Fluid Mech. 5 (1), 59–78.10.1146/annurev.fl.05.010173.000423Google Scholar
Fischer, H. B., List, E., Koh, R., Imberger, J. & Brooks, N. 1979 Mixing in Inland and Coastal Waters. Academic Press.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Grubišić, V., Smith, R. B. & Schär, C. 1995 The effect of bottom friction on shallow-water flow past an isolated obstacle. J. Atmos. Sci. 52 (11), 1985–2005.Google Scholar
Hoffman, M. D. & Gelman, A. 2014 The no-u-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J. Machine Learning Res. 15 (1), 1593–1623.Google Scholar
Ingram, R. G. & Chu, V. H. 1987 Flow around islands in Rupert Bay: an investigation of the bottom friction effect. J. Geophys. Res. 92 (C13), 14521–14533.Google Scholar
Isaksen, A., McMillan, L. & Gortler, S. J. 2000 Dynamically reparameterized light fields. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, pp. 297–306. ACM Press/Addison-Wesley Publishing Co. Google Scholar
Jenner, K. C. S., Jenner, M. N. & McCabe, K. A. 2001 Geographical and temporal movements of humpback whales in western Australian waters. APPEA J. 38 (1), 692–707.Google Scholar
Jensen, B. L., Sumer, B. M. & Fredsøe, J. 1989 Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 206, 265–297.Google Scholar
Johnston, D. W. & Read, A. J. 2007 Flow-field observations of a tidally driven island wake used by marine mammals in the bay of fundy, Canada. Fish. Oceanogr. 16 (5), 422–435.Google Scholar
Keane, R. D. & Adrian, R. J. 1992 Theory of cross-correlation analysis of PIV images. Appl. Sci. Res. 49 (3), 191–215.Google Scholar
Lloyd, P. M. & Stansby, P. K. 1997 Shallow-water flow around model conical islands of small side slope. II. Submerged. J. Hydraul. Engng 123 (12), 1068–1077.Google Scholar
Lloyd, P. M., Stansby, P. K. & Chen, D. 2001 Wake formation around islands in oscillatory laminar shallow-water flows. Part 1. Experimental investigation. J. Fluid Mech. 429, 217–238.10.1017/S0022112000002822Google Scholar
Moffat, R. J. 1988 Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1 (1), 3–17.10.1016/0894-1777(88)90043-XGoogle Scholar
Negretti, M. E., Vignoli, G., Tubino, M. & Brocchini, M. 2006 On shallow-water wakes: an analytical study. J. Fluid Mech. 567, 457–475.Google Scholar
Pattiaratchi, C., James, A. & Collins, M. 1987 Island wakes and headland eddies: a comparison between remotely sensed data and laboratory experiments. J. Geophys. Res. 92 (C1), 783–794.Google Scholar
Pingree, R. D. & Maddock, L. 1980 The effects of bottom friction and earth’s rotation on an island’s wake. J. Mar. Biol. Assoc. U.K. 60 (2), 499–508.10.1017/S0025315400028514Google Scholar
Raffel, M., Willert, C. & Wereley, S. 2007 Particle Image Velocimetry: A Practical Guide. Springer.Google Scholar
Riegels, F. 1938 Zur kritik des Hele-Shaw–Versuchs. Z. Angew. Math. Mech. 18 (2), 95–106.Google Scholar
Salvatier, J., Wiecki, T. V. & Fonnesbeck, C. 2016 Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2, e55.Google Scholar
Scarano, F. & Poelma, C. 2009 Three-dimensional vorticity patterns of cylinder wakes. Exp. Fluids 47 (1), 69–83.Google Scholar
Signell, R. P. & Geyer, W. R. 1991 Transient eddy formation around headlands. J. Geophys. Res. 96 (C2), 2561–2575.Google Scholar
Soulsby, R. L. 1983 The bottom boundary layer of shelf seas. In Physical Oceanography of Coastal and Shelf Seas (ed. Johns, B.), Elsevier Oceanography Series, vol. 35, chap. 5, pp. 189–266. Elsevier.Google Scholar
Sumer, B. M. & Fredsøe, J. 2006 Hydrodynamics Around Cylindrical Strucures, Advanced Series on Ocean Engineering, vol. 26. World Scientific Pub Co Inc. Google Scholar
Vaish, V., Garg, G., Talvala, E., Antunez, E., Wilburn, B., Horowitz, M. & Levoy, M. 2005 Synthetic aperture focusing using a shear-warp factorization of the viewing transform. In 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05)-Workshops, pp. 129–129. IEEE.Google Scholar
Westerweel, J. 1997 Fundamentals of digital particle image velocimetry. Meas. Sci. Technol. 8 (12), 1379–1392.Google Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39 (6), 1096–1100.10.1007/s00348-005-0016-6Google Scholar
White, L. & Wolanski, E. 2008 Flow separation and vertical motions in a tidal flow interacting with a shallow-water island. Estuar. Coast. Shelf Sci. 77 (3), 457–466.10.1016/j.ecss.2007.10.003Google Scholar
Williamson, C. H. K. 1985 Sinusoidal flow relative to circular cylinders. J. Fluid Mech. 155, 141–174.Google Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.Google Scholar
Wolanski, E., Asaeda, T., Tanaka, A. & Deleersnijder, E. 1996 Three-dimensional island wakes in the field, laboratory experiments and numerical models. Cont. Shelf Res. 16 (11), 1437–1452.Google Scholar
Wolanski, E., Brinkman, R., Spagnol, S., McAllister, F., Steinberg, C., Skirving, W. & Deleersnijder, E. 2003 Merging scales in models of water circulation: perspectives from the great barrier reef. In Advances in Coastal Modeling (ed. Lakhan, V. C.), Elsevier Oceanography Series, vol. 67, chap. 15, pp. 411–429. Elsevier.Google Scholar
Wolanski, E. & Hamner, W. M. 1988 Topographically controlled fronts in the ocean and their biological influence. Science 241 (4862), 177–181.Google Scholar
Wolanski, E., Imberger, J. & Heron, M. L. 1984 Island wakes in shallow coastal waters. J. Geophys. Res. 89 (C6), 10553–10569.Google Scholar
Supplementary material: File

Branson et al. supplementary material

Branson et al. supplementary material 1

Download Branson et al. supplementary material(File)
File 245.3 KB