Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pizzo, N. E.
and
Melville, W. Kendall
2016.
Wave modulation: the geometry, kinematics, and dynamics of surface-wave packets.
Journal of Fluid Mechanics,
Vol. 803,
Issue. ,
p.
292.
Deike, Luc
Pizzo, Nick
and
Melville, W. Kendall
2017.
Lagrangian transport by breaking surface waves.
Journal of Fluid Mechanics,
Vol. 829,
Issue. ,
p.
364.
Chavarria, Gerardo Ruiz
Le Gal, Patrice
and
Le Bars, Michael
2018.
Geometrical focusing of surface waves.
Physical Review Fluids,
Vol. 3,
Issue. 9,
Yang, Zixuan
Deng, Bing-Qing
and
Shen, Lian
2018.
Direct numerical simulation of wind turbulence over breaking waves.
Journal of Fluid Mechanics,
Vol. 850,
Issue. ,
p.
120.
Niewiarowski, Alexander
Adriaenssens, Sigrid
Pauletti, Ruy Marcelo
Addi, Khalid
and
Deike, Luc
2018.
Modeling underwater cable structures subject to breaking waves.
Ocean Engineering,
Vol. 164,
Issue. ,
p.
199.
Khait, A.
and
Shemer, L.
2018.
On the kinematic criterion for the inception of breaking in surface gravity waves: Fully nonlinear numerical simulations and experimental verification.
Physics of Fluids,
Vol. 30,
Issue. 5,
De Vita, Francesco
Verzicco, Roberto
and
Iafrati, Alessandro
2018.
Breaking of modulated wave groups: kinematics and energy dissipation processes.
Journal of Fluid Mechanics,
Vol. 855,
Issue. ,
p.
267.
Steinmann, Thomas
Arutkin, Maxence
Cochard, Précillia
Raphaël, Elie
Casas, Jérôme
and
Benzaquen, Michael
2018.
Unsteady wave pattern generation by water striders.
Journal of Fluid Mechanics,
Vol. 848,
Issue. ,
p.
370.
Sinha, Nityanand
and
Golshan, Roozbeh
2018.
Material Transport under a Wave Train in Interaction with Constant Wind: A Eulerian RANS Approach Combined with a Lagrangian Particle Dispersion Model.
Fluids,
Vol. 3,
Issue. 2,
p.
40.
Seiffert, Betsy R.
and
Ducrozet, Guillaume
2018.
Simulation of breaking waves using the high-order spectral method with laboratory experiments: wave-breaking energy dissipation.
Ocean Dynamics,
Vol. 68,
Issue. 1,
p.
65.
Thorpe, S. A.
2018.
Models of energy loss from internal waves breaking in the ocean.
Journal of Fluid Mechanics,
Vol. 836,
Issue. ,
p.
72.
Chen, Haifei
and
Zou, Qingping
2018.
Characteristics of Wave Breaking and Blocking by Spatially Varying Opposing Currents.
Journal of Geophysical Research: Oceans,
Vol. 123,
Issue. 5,
p.
3761.
Lenain, Luc
Pizzo, Nick
and
Melville, W. Kendall
2019.
Laboratory studies of Lagrangian transport by breaking surface waves.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
Reichl, Brandon G.
and
Li, Qing
2019.
A Parameterization with a Constrained Potential Energy Conversion Rate of Vertical Mixing Due to Langmuir Turbulence.
Journal of Physical Oceanography,
Vol. 49,
Issue. 11,
p.
2935.
Kalisch, Henrik
Ricchiuto, Mario
Bonneton, Philippe
Colin, Mathieu
and
Lubin, Pierre
2019.
Introduction to the Special Issue on Breaking Waves.
European Journal of Mechanics - B/Fluids,
Vol. 73,
Issue. ,
p.
1.
Pizzo, Nick
and
Kendall Melville, W.
2019.
Focusing deep-water surface gravity wave packets: wave breaking criterion in a simplified model.
Journal of Fluid Mechanics,
Vol. 873,
Issue. ,
p.
238.
Cui, Fangda
Geng, Xiaolong
Robinson, Brian
King, Thomas
Lee, Kenneth
and
Boufadel, Michel C.
2020.
Oil Droplet Dispersion under a Deep-Water Plunging Breaker: Experimental Measurement and Numerical Modeling.
Journal of Marine Science and Engineering,
Vol. 8,
Issue. 4,
p.
230.
Lin, Shangfei
Sheng, Jinyu
and
Xing, Jiuxing
2020.
Performance Evaluation of Parameterizations for Wind Input and Wave Dissipation in the Spectral Wave Model for the Northwest Atlantic Ocean.
Atmosphere-Ocean,
Vol. 58,
Issue. 4,
p.
258.
Xu, Yuanyuan
Liang, Shuxiu
Sun, Zhaochen
Xue, Qingren
and
Bi, Xiaoqi
2020.
An experimental comparison of the velocities and energies of focused spilling waves in deep water.
Ocean Dynamics,
Vol. 70,
Issue. 7,
p.
863.
Pizzo, Nick
Murray, Ethan
Smith, David Llewellyn
and
Lenain, Luc
2021.
The role of bandwidth in setting the breaking slope threshold of deep-water focusing wave packets.
Physics of Fluids,
Vol. 33,
Issue. 11,
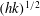 $(hk)^{1/2}$, where
$(hk)^{1/2}$, where 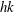 $hk$ is the local slope at breaking. This model is examined using direct numerical simulations of breaking waves solving the full two-phase air–water Navier–Stokes equations, as well as the limited available laboratory data, and good agreement is found for strong breaking waves.
$hk$ is the local slope at breaking. This model is examined using direct numerical simulations of breaking waves solving the full two-phase air–water Navier–Stokes equations, as well as the limited available laboratory data, and good agreement is found for strong breaking waves.


