Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-01T07:42:06.307Z Has data issue: false hasContentIssue false
  • English
  • Français

The critical layer in linear-shear boundary layers over acoustic linings

Published online by Cambridge University Press:  31 August 2012

E. J. Brambley ,
M. Darau  and
S. W. Rienstra
E. J. Brambley*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
M. Darau
Affiliation:
Department of Mathematics and Computer Science, Eindhoven University of Technology, PO Box 513, 5600 MB, Eindhoven, The Netherlands
S. W. Rienstra
Affiliation:
Department of Mathematics and Computer Science, Eindhoven University of Technology, PO Box 513, 5600 MB, Eindhoven, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Acoustics within mean flows are governed by the linearized Euler equations, which possess a singularity wherever the local mean flow velocity is equal to the phase speed of the disturbance. Such locations are termed critical layers, and are usually ignored when estimating the sound field, with their contribution assumed to be negligible. This paper studies fully both numerically and analytically a simple yet typical sheared ducted flow in order to investigate the influence of the critical layer, and shows that the neglect of critical layers is sometimes, but certainly not always, justified. The model is that of a linear-then-constant velocity profile with uniform density in a cylindrical duct, allowing exact Green’s function solutions in terms of Bessel functions and Frobenius expansions. 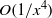For sources outside the sheared flow, the contribution of the critical layer is found to decay algebraically along the duct as , where is the distance downstream of the source. For sources within the sheared flow, the contribution from the critical layer is found to consist of a non-modal disturbance of constant amplitude and a disturbance decaying algebraically as 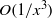. For thin boundary layers, these disturbances trigger the inherent convective instability of the flow. Extra care is required for high frequencies as the critical layer can be neglected only in combination with a particular downstream pole. The advantages of Frobenius expansions over direct numerical calculation are also demonstrated, especially with regard to spurious modes around the critical layer.

JFM classification

Acoustics: Aeroacoustics Waves/Free-surface Flows: Critical layers Boundary Layers: Pipe flow boundary layer
Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 545 - 568
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions, 9th edn. Dover.Google Scholar
2. Amos, D. E. 1986 Algorithm 644: a portable package for Bessel functions of a complex argument and nonnegative order. ACM Trans. Math. Softw. 12, 265–273.CrossRefGoogle Scholar
3. Boyer, G., Piot, E. & Brazier, J. P. 2011 Theoretical investigation of hydrodynamic surface mode in a lined duct with sheared flow and comparison with experiment. J. Sound Vib. 330, 1793–1809.CrossRefGoogle Scholar
4. Brambley, E. J. 2009 Fundamental problems with the model of uniform flow over acoustic linings. J. Sound Vib. 322, 1026–1037.CrossRefGoogle Scholar
5. Brambley, E. J. 2011 a Surface modes in sheared flow using the modified Myers boundary condition. AIAA Paper 2011-2736.CrossRefGoogle Scholar
6. Brambley, E. J. 2011b A well-posed boundary condition for acoustic liners in straight ducts with flow. AIAA J. 49 (6), 1272–1282.CrossRefGoogle Scholar
7. Brambley, E. J., Darau, M. & Rienstra, S. W. 2011The critical layer in sheared flow. AIAA Paper 2011-2806.Google Scholar
8. Brambley, E. J. & Peake, N. 2006 Classification of aeroacoustically relevant surface modes in cylindrical lined ducts. Wave Motion 43, 301–310.CrossRefGoogle Scholar
9. Brooks, C. J. & McAlpine, A. 2007 Sound transmission in ducts with sheared mean flow. AIAA Paper 2007-3545.CrossRefGoogle Scholar
10. Campos, L. M. B. C. & Kobayashi, M. H. 2000 On the reflection and transmission of sound in a thick shear layer. J. Fluid Mech. 424, 303–326.CrossRefGoogle Scholar
11. Campos, L. M. B. C. & Kobayashi, M. H. 2008 On the propagation of sound in a high-speed non-isothermal shear flow. Intl J. Aeroacoust. 8, 199–230.CrossRefGoogle Scholar
12. Campos, L. M. B. C. & Kobayashi, M. H. 2010 Sound transmission from a source outside a nonisothermal boundary layer. AIAA J. 48 (5), 878–892.CrossRefGoogle Scholar
13. Campos, L. M. B. C. & Oliveira, J. M. G. S. 2011 On the acoustic modes in a duct containing a parabolic shear flow. J. Sound Vib. 330, 1166–1195.CrossRefGoogle Scholar
14. Campos, L. M. B. C., Oliveira, J. M. G. S. & Kobayashi, M. H. 1999 On sound propagation in a linear shear flow. J. Sound Vib. 219, 739–770.CrossRefGoogle Scholar
15. Campos, L. M. B. C. & Serrão, P. G. T. A. 1998 On the acoustics of an exponential boundary layer. Phil. Trans. R. Soc. Lond. A 356, 2335–2378.CrossRefGoogle Scholar
16. Campos, L. M. B. C. & Serrão, P. G. T. A. 2010 On the continuous spectrum of sound in sheared and swirling flows. AIAA Paper 2010-4033.CrossRefGoogle Scholar
17. Case, K. M. 1960 Stability of inviscid plane Couette flow. Phys. Fluids 3, 143–148.CrossRefGoogle Scholar
18. Félix, S. & Pagneux, V. 2007 Acoustic and hydrodynamic modes generated by a point source in a duct carrying a parallel shear flow. In Proceedings 19th International Congress on Acoustics, Madrid, 2–7 September.Google Scholar
19. Friedland, A. B. & Pierce, A. D. 1969 Reflection of acoustic pulses from stable and instable interfaces between moving fluids. Phys. Fluids 12, 1148–1159.CrossRefGoogle Scholar
20. Golubev, V. V. & Atassi, H. M. 1996 Sound propagation in an annular duct with mean potential swirling flow. J. Sound Vib. 198, 601–616.CrossRefGoogle Scholar
21. Heaton, C. J. & Peake, N. 2006 Algebraic and exponential instability of inviscid swirling flow. J. Fluid Mech. 565, 279–318.CrossRefGoogle Scholar
22. Huerre, P. 1980 The nonlinear stability of a free shear layer in the viscous critical layer regime. Phil. Trans. R. Soc. Lond. A 293 (1408), 643–672.Google Scholar
23. Huerre, P. & Scott, J. F. 1980 Effects of critical layer structure on the nonlinear evolution of waves in free shear layers. Proc. R. Soc. Lond. A 371 (1747), 509–524.Google Scholar
24. Ingard, U. 1959 Influence of fluid motion past a plane boundary on sound reflection, absorption, and transmission. J. Acoust. Soc. Am. 31, 1035–1036.CrossRefGoogle Scholar
25. Jones, D. S. 1977 The scattering of sound by a simple shear layer. Phil. Trans. R. Soc. Lond. A 284, 287–328.Google Scholar
26. Jones, D. S. & Morgan, J. D. 1972 The instability of a vortex sheet on a subsonic stream under acoustic radiation. Proc. Camb. Phil. Soc. 72, 465–488.CrossRefGoogle Scholar
27. Maslowe, S. A. 1986 Critical layers in shear flows. Annu. Rev. Fluid Mech. 18, 405–432.CrossRefGoogle Scholar
28. Munt, R. M. 1977 The interaction of sound with a subsonic jet issuing from a semi-infinite cylindrical pipe. J. Fluid Mech. 83, 609–640.CrossRefGoogle Scholar
29. Myers, M. K. 1980 On the acoustic boundary condition in the presence of flow. J. Sound Vib. 71, 429–434.CrossRefGoogle Scholar
30. Olivieri, O., McAlpine, A. & Astley, R. J. 2010 Determining the pressure modes at high frequencies in lined ducts with a shear flow. AIAA Paper 2010-3944.CrossRefGoogle Scholar
31. Pridmore-Brown, D. C. 1958 Sound propagation in a fluid flowing through an attenuating duct. J. Fluid Mech. 4, 393–406.CrossRefGoogle Scholar
32. Rayleigh, Lord 1896 The Theory of Sound, vol. 2 , Macmillan.Google Scholar
33. Rienstra, S. W. 1981 On the acoustical implications of vortex shedding from an exhaust pipe. J. Engng Ind. 103, 378–384.CrossRefGoogle Scholar
34. Rienstra, S. W. 2003 A classification of duct modes based on surface waves. Wave Motion 37, 119–135.CrossRefGoogle Scholar
35. Rienstra, S. W. 2006 Impedance models in time domain, including the extended Helmholtz resonator model. AIAA Paper 2006-2686.Google Scholar
36. Rienstra, S. W. & Darau, M. 2011 Boundary-layer thickness effects of the hydrodynamic instability along an impednace wall. J. Fluid Mech. 671, 559–573.CrossRefGoogle Scholar
37. Rienstra, S. W., Darau, M. & Brambley, E. J. 2012 The trailing vorticity field behind a line source in 2D incompressible linear shear flow. J. Fluid Mech. (submitted).CrossRefGoogle Scholar
38. Rienstra, S. W. & Tester, B. J. 2008 An analytic Green’s function for a lined circular duct containing uniform mean flow. J. Sound Vib. 317, 994–1016.CrossRefGoogle Scholar
39. Swinbanks, M. A. 1975 The sound field generated by a source distribution in a long duct carrying sheared flow. J. Sound Vib. 40, 51–76.CrossRefGoogle Scholar
40. Tam, C. K. W. & Auriault, L. 1998 The wave modes in ducted swirling flows. J. Fluid Mech. 371, 1–20.CrossRefGoogle Scholar
41. Vilenski, G. G. & Rienstra, S. W. 2007a Numerical study of acoustic modes in ducted shear flow. J. Sound Vib. 307, 610–626.CrossRefGoogle Scholar
42. Vilenski, G. G. & Rienstra, S. W. 2007b On hydrodynamic and acoustic modes in a ducted shear flow with wall lining. J. Fluid Mech. 583, 45–70.CrossRefGoogle Scholar