Article contents
Critical and near-critical reflections of near-inertial waves off the sea surface at ocean fronts
Published online by Cambridge University Press: 20 January 2015
Abstract
In a balanced oceanic front, the possible directions of the group velocity vector for internal waves depart from the classic Saint Andrew’s cross as a consequence of sloping isopycnals and the associated thermal wind shear. However, for waves oscillating at the Coriolis frequency 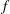 $f$, one of these directions remains horizontal, while the other direction allows for vertical propagation of energy. This implies the existence of critical reflections from the ocean surface, after which wave energy, having propagated from below, cannot propagate back down. This is similar to the reflection of internal waves, propagating in a quiescent medium, from a bottom that runs parallel to the group velocity vector. We first illustrate this phenomenon with a series of linear Boussinesq numerical experiments on waves with various frequencies,
$f$, one of these directions remains horizontal, while the other direction allows for vertical propagation of energy. This implies the existence of critical reflections from the ocean surface, after which wave energy, having propagated from below, cannot propagate back down. This is similar to the reflection of internal waves, propagating in a quiescent medium, from a bottom that runs parallel to the group velocity vector. We first illustrate this phenomenon with a series of linear Boussinesq numerical experiments on waves with various frequencies, 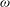 ${\it\omega}$, exploring critical (
${\it\omega}$, exploring critical (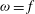 ${\it\omega}=f$), forward (
${\it\omega}=f$), forward (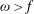 ${\it\omega}>f$), and backward (
${\it\omega}>f$), and backward (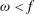 ${\it\omega}<f$) reflections. We then conduct the nonlinear equivalents of these simulations. In agreement with the classical case, backward reflection inhibits triadic resonances and does not exhibit prominent nonlinear effects, while forward reflection shows strong generation of harmonics that radiate energy away from the surface. Surprisingly though, critical reflections are associated with oscillatory motions that extend down from the surface. These motions are not freely propagating waves but instead take the form of a cluster of non-resonant triads which decays with depth through friction.
${\it\omega}<f$) reflections. We then conduct the nonlinear equivalents of these simulations. In agreement with the classical case, backward reflection inhibits triadic resonances and does not exhibit prominent nonlinear effects, while forward reflection shows strong generation of harmonics that radiate energy away from the surface. Surprisingly though, critical reflections are associated with oscillatory motions that extend down from the surface. These motions are not freely propagating waves but instead take the form of a cluster of non-resonant triads which decays with depth through friction.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 11
- Cited by



